Tarjan算法各种&RMQ& POJ 3694
关于tarjan 的思想可以在网上搜到,具体我也不太清楚,应该说自己理解也不深,下面是做题经验得到的一些模板。
其中有很多转载,包括BYVoid等,感谢让我转。。。望各路大神愿谅
有向图求连通分量的一般方法:
void Tarjan(u) {
dfn[u]=low[u]=++index
stack.push(u)
for each (u, v) in E {
if (v is not visted) {
tarjan(v)
low[u] = min(low[u], low[v])
}
else if (v in stack) { //可设置stack数组
low[u] = min(low[u], dfn[v])
}
}
if (dfn[u] == low[u]) { //u是一个强连通分量的根
repeat
v = stack.pop
print v
until (u== v)
} //退栈,把整个强连通分量都弹出来
//此时可为所弹出的联通分量标号,便于0重建图
} //复杂度是O(E+V)的
无相连通图割点满足条件 ( 重边对割点不影响 ,这很重要)
一个顶点u是割点,当且仅当满足(1)或(2)
(1) u为树根,且u有多于一个子树。
(2) u不为树根,且满足存在(u,v)为树枝边(或称父子边,即u为v在搜索树中的父亲),使得dfn(u)<=low(v)。
void tarjan(int x){
v[x]=;
dfn[x]=low[x]=++num;
for(int i=head[x];i;i=next[i])
if(!v[ver[i]]){
tarjan(ver[i]);
low[x]=min(low[x],low[ver[i]]);
if(dfn[x]<=low[ver[i]])
v[x]++;
}
else
low[x]=min(low[x],dfn[ver[i]]);
if((x==root&&v[x]>)||(x!=root&&v[x]>))
v[x]=;
else
v[x]=;//v[x]=2表示该点为割点,注意其中第一个点要特判
}
void tarjan(int u,int ufa)
{
int rootson=0;//根节点的儿子节点数目,如果大于1,则根节点是割点
low[u]=dfn[u]=++num;//标记次序的节点编号一定要从1开始
for(int i=head[u]; i!=-1; i=e[i].next)
{
int j=e[i].to;
if(!dfn[j])
{
if(u==root)//根的情况要特殊处理,j不可能等于root,j是u的子节点
{
if(++rootson>1) ans[u]=true;
}
tarjan(j,u);//u是j的父节点
low[u]=min(low[j],low[u]);//low值是更新当前的父节点,利用儿子节点的low来更新
if(u!=root&&dfn[u]<=low[j])//根的情况已经讨论,避免重复
ans[u]=true;//都是对目前传入的父亲节点进行讨论,不能置其子节点为true.
}
else if(j!=ufa)
low[u]=min(low[u],dfn[j]);
}
}
无相连通图(可能存在重边的情况下)桥
void tarjan(int u){
dfn[u]=low[u]=++clock;
for(int e=head[u];e!=-;e=edge[e].next){
int v=edge[e].v;
if(dfn[v]==-){
vis_e[e]=vis_e[e^]=true;
tarjan(v);
low[u]=min(low[u],low[v]);
if(dfn[u] >=low[v]){
// Union(u,v); 两点在同一个分量中,合并可得边双连通图
}
else{
is_bridge[e] = is_bridge[e^] = true;
}
}
else if(dfn[v] < dfn[u] && !vis_e[e]){
vis_e[e] = vis_e[e^] = true;
low[u]=min(low[u],dfn[v]);
}
}
}
把求桥和求割点合并在一个程序中(不考虑重边)
void Tarjan(int u, int father){ //father 是u的父节点
Father[u] = father;
int i,j,k;
low[u] = dfn[u] = nTime ++;
for( i = ;i < G[u].size() ;i ++ ) {
int v = G[u][i];
if( ! dfn[v]) {
Tarjan(v,u);
low[u] = min(low[u],low[v]);
}
else if( father != v ) //连到父节点的回边不考虑,否则求不出桥
low[u] = min(low[u],dfn[v]);
}
}
void Count(){ //计算割点和桥
int nRootSons = ; int i;
Tarjan(,);
for( i = ;i <= n;i ++ ) {
int v = Father[i];
if( v == )
nRootSons ++; //DFS树中根节点有几个子树
else {
if( dfn[v] <= low[i]) //判断割点条件
bIsCutVetext[v] = true;
}
}
if( nRootSons > ) //根结点至少有两个子树
bIsCutVetext[] = true;
for( i = ;i <= n;i ++ )
if( bIsCutVetext[i] ) //割点
cout << i << endl;
for( i = ;i <= n;i ++) {
int v = Father[i];
if(v > && dfn[v] < low[i]) // 割边
cout << v << "," << i <<endl;
}
}
求点双连通实际上是在求割点时得到的。(无重边)
对于点双连通分支,实际上在求割点的过程中就能顺便把每个点双连通分支求出。建立一个栈,存储当前双连通分支,在搜索图时,每找到一条树枝边或反向边,就把这条边加入栈中。如果遇到某时满足dfn(u)<=low(v),说明u是一个割点,同时把边从栈顶一个个取出,直到遇到了边(u,v),取出的这些边与其关联的点,组成一个点双连通分支。割点可以属于多个点双连通分支,其余点和每条边只属于且属于一个点双连通分支。
void Tarjan(int u, int father){
int i,j,k;
low[u] = dfn[u] = nTime ++;
for( i = ;i < G[u].size() ;i ++ ) {
int v = G[u][i];
if( ! dfn[v]) { //v没有访问过
//树边要入栈
Edges.push_back(Edge2(u,v));
Tarjan(v,u);
low[u] = min(low[u],low[v]);
Edge2 tmp(,);
if(dfn[u] <= low[v]) {
//从一条边往下走,走完后发现自己是割点,则栈中的边一定全是和自己在一个双连通分量里面
//根节点总是和其下的某些点在同一个双连通分量里面
cout << "Block No: " << ++ nBlockNo << endl;
do {
tmp = Edges.back();
Edges.pop_back ();
cout << tmp.u << "," << tmp.v << endl;
}while ( !(tmp.u == u && tmp.v == v) );
}
} // 对应if( ! dfn[v]) {
else {
if( v != father ) {//u连到父节点的回边不考虑
low[u] = min(low[u],dfn[v]);
if( dfn[u] > dfn[v])
//子孙连接到祖先的回边要入栈,但是子孙连接到自己的边,此处肯定已经入过栈了,不能再入栈
Edges.push_back(Edge2(u,v));
}
}
} //对应 for( i = 0;i < G[u].size() ;i ++ ) {
}
有重边
void Tarjan(int u, int father){
int i,j,k;
low[u] = dfn[u] = nTime ++;
for( each (u,v) ){
if( ! dfn[v]) { //v没有访问过
//树边要入栈
vis[e]=vis[e^]=true;
Edges.push_back(Edge2(u,v));
Tarjan(v,u);
low[u] = min(low[u],low[v]);
Edge2 tmp(,);
if(dfn[u] <= low[v]) {
//从一条边往下走,走完后发现自己是割点,则栈中的边一定全是和自己在一个双连通分量里面
//根节点总是和其下的某些点在同一个双连通分量里面
cout << "Block No: " << ++ nBlockNo << endl;
do {
tmp = Edges.back();
Edges.pop_back ();
cout << tmp.u << "," << tmp.v << endl;
}while ( !(tmp.u == u && tmp.v == v) );
//还应注意,一条边也是点双联通
}
} // 对应if( ! dfn[v]) {
else {
if( !vis[e] ) {//u连到父节点的回边不考虑
low[u] = min(low[u],dfn[v]);
if( dfn[u] > dfn[v])
//子孙连接到祖先的回边要入栈,但是子孙连接到自己的边,此处肯定已经入过栈了,不能再入栈
Edges.push_back(Edge2(u,v));
}
}
} //对应 for( i = 0;i < G[u].size() ;i ++ ) {
}
一个有桥的连通图,如何把它通过加边变成边双连通图?
方法为首先求出所有的桥,然后删除这些桥边,剩下的每个连通块都是一个双连通子图。把每个双连通子图收缩为一个顶点,再把桥边加回来,最后的这个图一定是一棵树,边连通度为1。
统计出树中度为1的节点的个数,即为叶节点的个数,记为leaf。则至少在树上添加(leaf+1)/2条边,就能使树达到边二连通,所以至少添加的边数就是(leaf+1)/2。具体方法为,首先把两个最近公共祖先最远的两个叶节点之间连接一条边,这样可以把这两个点到祖先的路径上所有点收缩到一起,因为一个形成的环一定是双连通的。然后再找两个最近公共祖先最远的两个叶节点,这样一对一对找完,恰好是(leaf+1)/2次,把所有点收缩到了一起。
LCA问题
LCA
Tarjan作为离线off-line算法,在程序开始前,需要将所有等待询问的节点对提前存储,然后程序从树根开始执行TarjanLCA()。假如有如下一棵多叉树
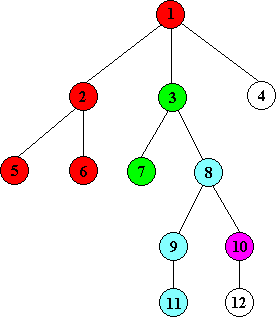
根据TarjanLCA的实现算法可以看出,只有当某一棵子树全部遍历处理完成后,才将该子树的根节点标记为黑色(初始化是白色),假设程序按上面的树形结构进行遍历,首先从节点1开始,然后递归处理根为2的子树,当子树2处理完毕后,节点2, 5, 6均为黑色;接着要回溯处理3子树,首先被染黑的是节点7(因为节点7作为叶子不用深搜,直接处理),接着节点7就会查看所有询问(7, x)的节点对,假如存在(7, 5),因为节点5已经被染黑,所以就可以断定(7, 5)的最近公共祖先就是find(5).ancestor,即节点1(因为2子树处理完毕后,子树2和节点1进行了union,find(5)返回了合并后的树的根1,此时树根的ancestor的值就是1)。 有人会问如果没有(7, 5),而是有(5, 7)询问对怎么处理呢?我们可以在程序初始化的时候做个技巧,将询问对(a, b)和(b, a)全部存储,这样就能保证完整性。
function TarjanLCA(u)
MakeSet(u);
u.ancestor := u;
for each v in u.children do
TarjanLCA(v);
Union(u,v);
Find(v).ancestor := u; //把v的父亲置为u
u.colour := black;
for each v such that {u,v} in P do // P 存储所有等待询问的节点对
if v.colour == black
print "Tarjan's Least Common Ancestor of " + u +
" and " + v + " is " + Find(v).ancestor + "." //此处一定是v
RMQ
LCA向RMQ转化
对有根树T进行DFS,将遍历到的结点按照顺序记下,我们将得到一个长度为2N – 1的序列,称之为T的欧拉序列F
每个结点都在欧拉序列中出现,我们记录结点u在欧拉序列中第一次出现的位置为pos(u)

此处要先介绍人ST算法:
ST算法是使用预处理来获得效率的。
预处理:
预处理使用DP的思想,f(i, j)表示[i, i+2^j - 1]区间中的最小值,我们可以开辟一个数组专门来保存f(i, j)的值。
例如,f(0, 0)表示[0,0]之间的最小值,就是num[0], f(0, 2)表示[0, 3]之间的最小值, f(2, 4)表示[2, 17]之间的最小值
注意, 因为f(i, j)可以由f(i, j - 1)和f(i+2^(j-1), j-1)导出, 而递推的初值(所有的f(i, 0) = i)都是已知的
所以我们可以采用自底向上的算法递推地给出所有符合条件的f(i, j)的值。
查询:
假设要查询从m到n这一段的最小值, 那么我们先求出一个最大的k, 使得k满足2^k <= (n - m + 1).
于是我们就可以把[m, n]分成两个(部分重叠的)长度为2^k的区间: [m, m+2^k-1], [n-2^k+1, n];
而我们之前已经求出了f(m, k)为[m, m+2^k-1]的最小值, f(n-2^k+1, k)为[n-2^k+1, n]的最小值
我们只要返回其中更小的那个, 就是我们想要的答案, 这个算法的时间复杂度是O(1)的.
例如, rmq(0, 11) = min(f(0, 3), f(4, 3))
void st(int n){
int i, j, k, m;
k = (int) (log((double)n) / log(2.0));
for(i = ; i < n; i++) {
f1[i][] = num[i]; //递推的初值
f2[i][] = num[i];
}
for(j = ; j <= k; j++) { //自底向上递推
for(i = ; i + ( << j) - < n; i++) {
m = i + ( << (j - )); //求出中间的那个值
f1[i][j] = mmax(f1[i][j-], f1[m][j-]);
f2[i][j] = mmin(f2[i][j-], f2[m][j-]);
}
}
}
查询
void rmq(int i, int j) {
int k = (int)(log(double(j-i+)) / log(2.0)), t1, t2; //用对2去对数的方法求出k
t1 = mmax(f1[i][k], f1[j - (<<k) + ][k]);
t2 = mmin(f2[i][k], f2[j - (<<k) + ][k]);
printf("%d\n",t1 - t2);
}
LCA转RMQ中
则LCA中求最近公共祖先就是在最先出现的位置区间内求
求该深度序列深度最小值所对应的欧拉序列的点
//这个算法是利用了RMQ的思想,DP记录的是某段区间最小值的位置
void st(){
int i, j, k, m;
for(i=;i<=time;i++)
dp[i][]=i;
for(j=;(<<j)<=time;j++)
{
for(i=;i+(<<j)-<=time;i++)
{
if(depth[dp[i][j-]]<depth[dp[i+(<<(j-))][j-]])
dp[i][j]=dp[i][j-];
else
dp[i][j]=dp[i+(<<(j-))][j-];
}
}
}
//depth是深度序列
int rmq(int i, int j) {
int k = (int)(log(double(j-i+)) / log(2.0));
return k;
}
//squ是欧拉序列
int find(int s,int x){
int t1=first[s],t2=first[x]; // first是首次出现的位置
if(t1>t2){
int tmp=t1;
t1=t2;
t2=tmp;
}
int t=rmq(t1,t2); int ancestor;
if(depth[dp[t1][t]]<depth[dp[t2-(<<t)+][t]])
ancestor=squ[dp[t1][t]];
else
ancestor=squ[dp[t2-(<<t)+][t]];
return ancestor;
}
POJ 3694
求出所有的桥后缩点,则变成树。树的每一条边均为桥。
那么,要求增加一条边后还剩多少条桥,可知,两点到其LCA的路径均不成为桥。
但此处求LCA时有一个小技巧,因为要统计数目。所以,可能通过减少深度的操作完成。先把两点提至同一深度,然后再两点同时向根回溯,每经过边则减少一条桥。
#include <iostream>
#include <cstdio>
using namespace std;
const int MAXN=;
const int MAXM=; struct {
int u,v;
int next;
}edge[MAXM*],tree[MAXM*];
int tot,n,m,clock,k;
int head[MAXN],dfn[MAXN],low[MAXN],pre[MAXN],rank[MAXN];
bool vis_e[MAXM*],is_bridge[MAXM*],visT[MAXN];
int depth[MAXN],p[MAXN],head_T[MAXN];
void addedge(int u,int v){
vis_e[tot]=is_bridge[tot]=false;
edge[tot].u=u;
edge[tot].v=v;
edge[tot].next=head[u];
head[u]=tot++;
vis_e[tot]=is_bridge[tot]=false;
edge[tot].u=v;
edge[tot].v=u;
edge[tot].next=head[v];
head[v]=tot++;
} void addTree(int u,int v){
//vis_e[tot]=false;
tree[tot].u=u;
tree[tot].v=v;
tree[tot].next=head_T[u];
head_T[u]=tot++;
// vis_e[tot]=false;
tree[tot].u=v;
tree[tot].v=u;
tree[tot].next=head_T[v];
head_T[v]=tot++;
} int find(int x){
int r=x;
while(pre[r]!=-)
r=pre[r];
while(pre[x]!=-){
int tx=pre[x];
pre[x]=r;
x=tx;
}
return r;
}
int min(int a,int b){
if(a<b)return a;
return b;
} void Union(int x,int y){
int xx=find(x);
int yy=find(y);
if(rank[xx]>rank[yy])
pre[yy]=xx;
else if(rank[xx]<rank[yy])
pre[xx]=yy;
else {
pre[xx]=yy;
rank[yy]++;
}
} void tarjan(int u){
dfn[u]=low[u]=++clock;
for(int e=head[u];e!=-;e=edge[e].next){
int v=edge[e].v;
if(dfn[v]==-){
vis_e[e]=vis_e[e^]=true;
tarjan(v);
low[u]=min(low[u],low[v]);
if(dfn[u] >=low[v]){
// cout<<u<<' '<<v<<endl;
Union(u,v);
}
else{
is_bridge[e] = is_bridge[e^] = true;
// cout<<u<<' '<<v<<endl;
}
}
else if(dfn[v] < dfn[u] && !vis_e[e]){
vis_e[e] = vis_e[e^] = true;
low[u]=min(low[u],dfn[v]);
}
}
} int count;
void dfs(int r,int c){
int i,j,u,v;
depth[r]=c;
visT[r]=true;
count++;
for(i=head_T[r];i!=-;i=tree[i].next){
v=tree[i].v;
//cout<<v<<endl;
if(!visT[v]){
// cout<<v<<endl;
p[v]=r;
dfs(v,c+);
}
}
visT[r]=false;
} void lca(int x,int y){
if(depth[x]>depth[y]){
while(depth[x]!=depth[y]){
if(!visT[x]){
visT[x]=true;
count--;
}
x=p[x];
}
}
if(depth[x]<depth[y]){
while(depth[x]!=depth[y]){
if(!visT[y]){
visT[y]=true;
count--;
}
y=p[y];
}
}
if(depth[x]==depth[y]){
while(x!=y){
if(!visT[x]){
visT[x]=true;
count--;
}
x=p[x];
if(!visT[y]){
visT[y]=true;
count--;
}
y=p[y];
}
}
} int main(){
int u,v,j,i; int tt=;
while(scanf("%d%d",&n,&m)!=EOF){
tt++;
if(!n&&!m) break;
for(i=;i<=n;i++){
head[i]=pre[i]=head_T[i]=-;
dfn[i]=low[i]=-;
rank[i]=;
p[i]=-;
}
tot=; clock=;
for(i=;i<=m;i++){
scanf("%d%d",&u,&v);
addedge(u,v);
}
tarjan();
// cout<<"YES"<<endl;
// system("pause");
tot=;
int root;
for(i=;i<=n;i++){
visT[i]=false;
for(j=head[i];j!=-;j=edge[j].next){
v=edge[j].v;
if(is_bridge[j]){
int x=find(i);
int y=find(v);
// cout<<x<<' '<<y<<endl;
root=x;
addTree(x,y);
is_bridge[j]=is_bridge[j^]=false;
}
}
}
// cout<<"YES"<<endl;
count=;
dfs(root,); count--;
// cout<<"YES"<<endl;
scanf("%d",&k);
printf("Case %d:\n",tt);
while(k--){
scanf("%d%d",&u,&v);
int x=find(u);
int y=find(v);
if(x==y||(visT[x]&&visT[y]))
printf("%d\n",count);
else{
lca(x,y);
printf("%d\n",count);
}
}
printf("\n");
}
return ;
}
最新文章
- Unity3d学习 预设体(prefab)的一些理解
- Android 四大组件之再论service
- Linux编程 ---- dup函数
- verilog中的for循环问题
- 【干货】国外程序员整理的 C++ 资源大全
- Ubuntu 16.04 Mxnet CPU 版本安装
- 让一个div可以编辑加上contenteditable=true 复制来的内容带有样式,需要清除复制的样式
- mysql优化方法
- 深入js的面向对象学习篇(封装是一门技术和艺术)——温故知新(二)
- 详解 CSS 属性 - 伪类和伪元素的区别[转]
- ApiDemos示例学习(1)——ApiDemos示例的导入
- Jsp中使用数据库连接池.
- Struts2 设置global timer
- 1045-access denied for user 'root'@
- SQLServer 索引总结
- SPOJ 1812 Longest Common Substring II
- windows下python3.5使用pip离线安装whl包
- Spring Beans和依赖注入
- node启动服务报错Node.js Error: Cannot find module express
- 循序渐进学.Net Core Web Api开发系列【10】:使用日志