B-树 分合之道
P.s:在代码里会同时用到向量和B-树的search,insert, remove,具体调用的是哪个结构的函数结合上下文就能看懂。
根据上一篇文章,我们对于这棵树的大致结构已经明了,那该如何有效利用并且根据情况维护它呢?这次用模板类写,方便日后不同数据类型的使用
先给出类型声明和模板类
#include "Vector.h" //这是之前写的向量结构,在我的github上,自己写的接口更适合这里实现B树,当然也可以用STL里的。
#include <cstdio>
using namespace std; #ifndef B__tree_h
#define B__tree_h #define Posi(T) BTrNode<T>* //B-树节点位置 template <typename T> struct BTrNode{
Posi(T) par;
Vector<T> key;// 存放关键字的向量
Vector< Posi(T) > child; //存放孩子指针的向量,比key多1 //2种构造函数,BTrNode只能作为根节点创建
BTrNode(){ par=NULL; child.push_back(NULL);} BTrNode( T key, Posi(T) lc=NULL, Posi(T) rc=NULL ){
par=NULL;
key.insert(,key);
child.insert(,lc); child.insert(,rc);
if(lc) lc->par=this; if(rc) rc->par=this;
}
}; #endif /* B__tree_h */
类:
#include "Vector.h"
#include "B- tree.h"
#include <cstdio>
using namespace std; template <typename T>
class BTree {
protected:
int _size,_order; //关键码总数,阶次,至少为3
Posi(T) _root;
Posi(T) hot;// BTree::search()最后访问的非空节点位置,相当于浮标 //core section
void solveOverFlow(Posi(T) ); //处理上溢的分裂
void solveUnderFlow(Posi(T) );//处理下溢的合并、旋转 public:
BTree(int assign=): _order(assign),_size(){ _root=new BTrNode<T>();}//默认起码3阶
~BTree(){ if(_root) release(_root);} Posi(T) search(const T & value);
bool insert(const T & value);
bool remove(const T & value);
int const size() {return _size; } //keep _size can not be changed in external
int const order(){return _order; } //ditto
Posi(T)& root(){ return _root;}
bool empty() {return !_root;} };
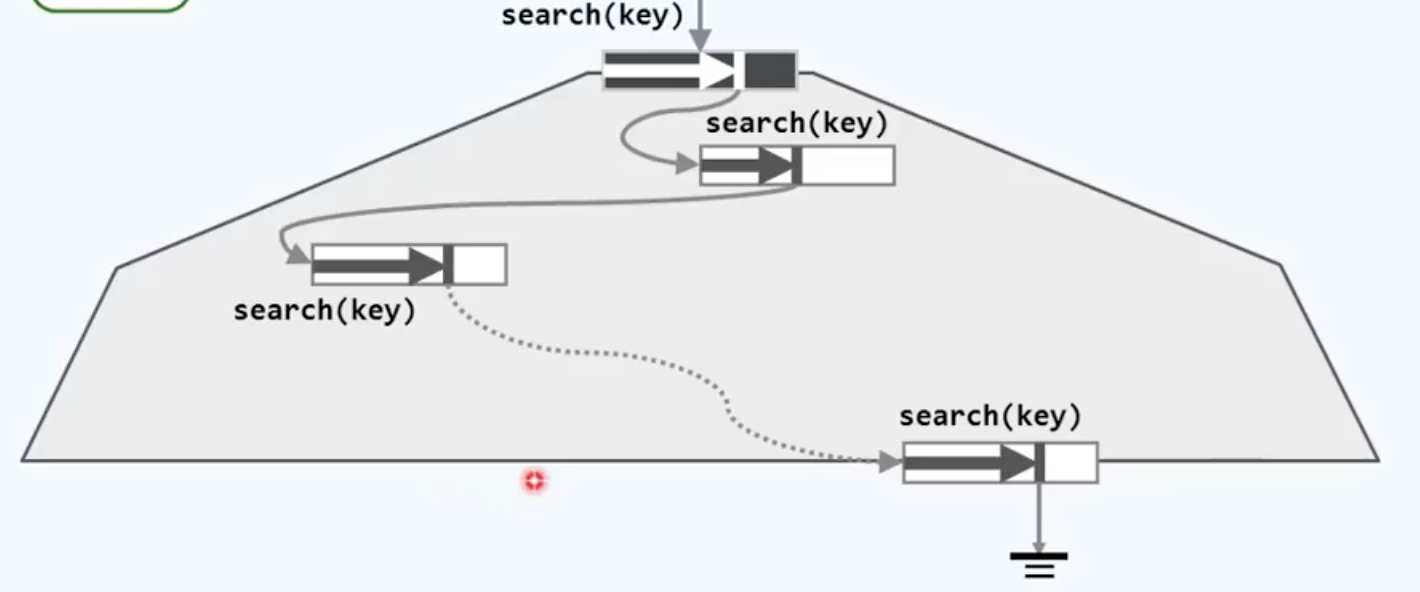
首先来看如何在B树中有效查找,不然万事皆休。下面是一颗典型的B树

之前说过B树中所存放的词条很多,内存放不下,只能放在外部存储里,只需要将有需要的节点载入内存,其他的先在外面等着,通过这种策略尽可能地减少IO。对于一棵处于活跃状态的B树而言,根节点已经常驻内存了。现在我们要查找一个值,v,先对根扫描一遍,找到则已,找不到的话,会暂停在一个位置$r$,对应记录了下一层的引用,那按图索骥往下找一层,去往下找第$r+1$个孩子,代价是一次IO

找不到就再往下一层,直到抵达叶节点,如果还找不到,那下面就是外部节点了,这时候就可以报告查找失败了。还有另外一种情况——外部引用实际上指向一棵存放于更低层次存储级别上的B树,这也是叫做外部节点的原因,因为借助它们可以把存放在不同存储级别的B树连接起来,构成更大的B树。不过现在我们只着眼于这个局部,先不考虑其他层次的小B-树。
纵观全局,查找其实就是由一系列在内存中的顺序查找 + 一系列的IO操作,间隔组成的操作序列。可以得出一个推论:失败查找必然终止于外部节点。
尽管key和child是按向量组织,应该是对齐的,但是方便理解节点内某个关键字和左右孩子之间的关系,我们从逻辑上将其错位排列。

之前写的向量search(a)语义是返回$\leq a$的最大值,因此如果查找失败于第r个关键码,那目标肯定在他后面,所以顺着r+1往下找。要记住这个关系:第r个关键码以及第r+1个后代引用。因此代码兑现如下:
template <typename T>
Posi(T) BTree<T>::search(const T & e) {
Posi(T) cur = _root; hot = NULL; //从根开始
while ( cur ) {
Rank r = cur -> key.search(e); //顺序查找
if(r >= && e == cur -> key[r]) return cur; //如果成功则返回当前引用
hot = cur; cur = cur -> child[r+];//更新hot,转到下一层子树,把根载入内存
}//走到这里时 !cur为真,说明抵达外部节点
return NULL;
}
很显然在这个查找过程中我们用到了Decrease and Conquer的思想,而且每一层只会涉及一个内部节点,最终制约效率的心腹大患还是高度。引起查找开销主要是两个部分:不同层的IO和内部节点的扫描,由于每次查找时在同一高度只访问1个节点,这就决定了对于高度为h的B-树,外存访问不会超过$O\left( h-1 \right)$次。而因为B-树的分支数并不固定,所以树高并不完全取决于关键码总数N。对于M阶N个关键码的树,他的高度h在什么范围变化呢?我们需要明确的知道这个关系。
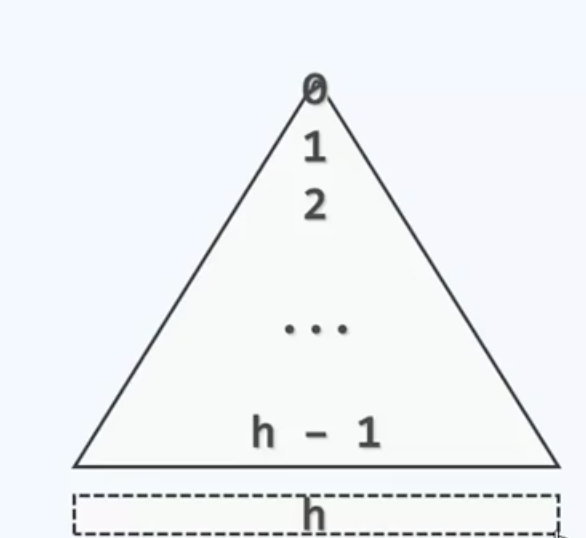
高度h和总关键码数量N之间的关系渐进来看大致是$h=O\left( \log N \right)$,但是具体范围呢?现在我们来对树高的上下确界做一个计算。
对于一颗确定M阶N个关键码的树,求一下高度的最大值,当关键码数目固定时,为了让高度尽可能大,内部节点应该存尽量少的关键字,分支数尽可能少,取定义的下限$\left\lceil \frac{M}{2} \right\rceil$,顶层只包含树根$n_{0}\; =\; 1$,树根下面最少可以有两个孩子
$n_{1}\; =\; 2$,
$n_{2}\; =\; 2\; \cdot \left\lceil \frac{M}{2} \right\rceil$
$n_{3}\; =\; 2\; \cdot \left\lceil \frac{M}{2} \right\rceil^{2}$
….
$n_{k}\; =\; 2\; \cdot \left\lceil \frac{M}{2} \right\rceil^{k-1}$
这个式子适用于所有的情况。
再来看外部节点,他们对应于所有查找失败的情况,比成功查找的情形多1,而成功查找则是所有关键码的总数N。这层所含的节点数最少就是$2\cdot \; \left\lceil \frac{M}{2} \right\rceil^{h-1}$,这是外部节点的最小值。关于B树有一条规律,是这样的,如果一棵B树中包含的真实关键码数为N的话,那么对应的外部节点总数是$N+1$,具体到这里也就是$N\; +\; 1\; =\; n_{h}$,有了前面的分析,相比这个关系就好理解了。因此我们得到$N\; +\; 1\; =\; n_{h}\; \geq \; 2\cdot \left\lceil \frac{m}{2} \right\rceil^{h-1}\; $这个式子
然后整理一下就得到了关于h的显式不等式$h\; \leq \; 1\; +\; \log _{\left\lceil \frac{M}{2} \right\rceil}\left\lfloor \frac{N+1}{2} \right\rfloor\; =\; O\left( \log _{M}N \right)\; $
现在再来求一下高度的下界。当关键码数目固定时,为了让高度尽可能小,内部节点应该存更多的关键字。根据定义各个高度的节点数目最多是
$n_{0}\; =\; 1$
$n_{1}\; =\; M$
$n_{2}\; =\; M^{2}$
…
$n_{h}\; =\; M^{h-1}$
于是我们得到$N+1\; =\; n_{h}\; \leq \; M^{h}$
稍作整理得:$ h\; \; \geq \; \; \log _{M}\left( \; N\; +\; 1\; \right)\; =\; \Omega \left( \; \log _{M}N\; \right) $。
由此把两个部分整合起来我们就有了关于B-树高度的确界:$ \log _{M}\left( \; N\; +\; 1\; \right)\; \; \leq \; \; h\; \; \leq \; \log _{\left\lceil \frac{M}{2} \right\rceil}\left\lfloor \frac{N+1}{2} \right\rfloor\; +\; 1 $ 。相对于常规的BBST(Balanced Binary Search Tree),做一个树高的比较$\; \frac{\log _{\left\lceil \frac{M}{2} \right\rceil}\left( \frac{N}{2} \right)}{\log _{2}N}\; $,假如说M=256,B-树的高度(IO次数)大约是BBST的$\frac{1}{7}$。我们此前有过关于大学4年与30年的比喻,差了7倍,这个结果背后的原因正在于此。
下面说插入算法,我们要在这个位置插入一个关键字

变成这样:

具体过程就是找到合适的位置,放入key向量里,同时child向量对应位置加一个空指针,根据情况做分裂操作,保证插入后内部节点所含的关键码仍符合B树定义。
template <typename T>
bool BTree<T>::insert(const T & e){
Posi(T) t = search(e);//这里调用的是B树的search接口
if(t) return false; //如果已经存在就什么也不做 Rank r = hot->key.search(e);//在hot中确定插入位置,hot指向的是一个叶节点。search in vector
hot->key.insert(r+,e);//把目标关键码放在向量对应位置
hot->child.insert(r+,NULL);//创建一个空子树指针,视作右侧分支
_size++;
solveOverFlow(hot);//如果发生overflow要进行一次分裂
return true;
}
具体的分裂规则是这样的,对发生overflow的节点(假设里面是$k_{0}\; ,\; k_{1}...\; k_{m-1}$)取中位数$mid\; =\; \; \frac{M}{2}$
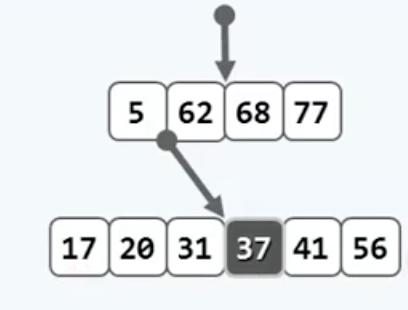
将对应的关键码$k_{mid}$上升一层,现在节点里剩下两组数,从中间分开的,然后把它们分别作为上升后的$k_{mid}$ 的左右孩子即可。
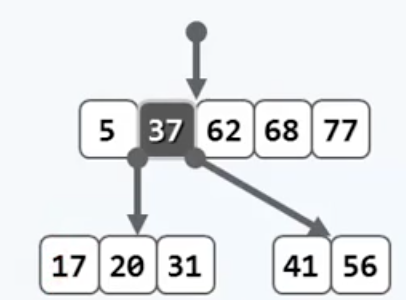
这个“上升”操作,实现起来也很方便,设当前溢出节点是v,父节点是p,只需要从v中删除那个中位数,然后把返回值压入p中关键字向量对应的位置即可,也就是p->key.insert(父节点的合适下标,v->key.remove(中位数下标)),然后让新旧节点互相连接一下就好了,这最后一步千万不能忘记。我第一次写的时候,上升完就美滋滋地走了也没再管,调bug的时候简直痛不欲生Orz
经此过程之后,新得到的两组关键码仍符合B树关于分支数的定义,在$\left\lceil \frac{M}{2} \right\rceil$ 到$M$之间,得益于这条精妙的规则,分裂操作就能在这个界限内游刃有余的进行。但是这一顿操作之后父节点同样有overflow的风险,继续调用这个过程就行了,如法炮制。一路向上传播,最坏情况下会到树根,这种情况就要小心了。

一旦树根处也溢出,我们仍要找出中位数序号的关键字,以此为界一分为二,让其自成节点,作为新的树根,这是导致B树增高的唯一情况。

通过以上分析可以看出,每层分裂操作至多1次,累计$\leq \; h$次,单次需要常数时间,那么总共的复杂度是$O\left( h \right)\; =\; O\left( \log _{M}N \right)$,这已经不慢了。实际上需要这么多次分裂的情况非常罕见,大多数时候时间主要消耗在对目标关键码的定位上。
总结一下,处理分裂的难点在于情况繁多,还必须不重不漏,我们来分类讨论吧。如上所述,提升节点之后有三种进一步的情况要考虑:父节点有空位,父节点没空位,或者根本没有父节点,自己就是根了。第一种情况把当前中间的关键码按次序插入父节点就行。第二种情况先把目标按次序插入父节点,然后把父节点作为参数传入分裂函数,转化为第一种情况。第三种,让被提升的关键码自成一节点即可。有了这个思路铺垫,我们来着手让它落地吧。
template <typename T>
void BTree<T>::solveOverFlow(Posi(T) current){
if(_order >= current->child.size()) return ; //判断当前节点是否上溢,无则返回
Rank mid=_order/; //作为枢纽 此时有这样的关系: _order = key.size() = child.size()-1
Posi(T) right=new BTrNode<T>(); // 新节点已经有一个空孩子 for (int i=; i<_order-mid-; i++) {//当前右侧的_order-s-1个孩子和关键码分裂为右侧节点right(以下简称r)
right->child.insert(i, current->child.remove(mid+));
right->key.insert(i,current->key.remove(mid+));
}
right->child[_order-mid-] =current->child.remove(mid+);//移动当前最靠右的孩子 if(right->child[])//如果right的孩子非空
for(int i=;i< _order-mid;i++)
right->child[i]->parent=right; //令他们的父节点统一指向自己,因为下面的都是外部节点了
Posi(T) p=current->par;
if(!p) { //这时候cur已经是根了,就执行对根分裂的步骤
_root=p=new BTrNode<T>();
p->child[]=current;
current->par=p;
}
Rank r=+p->key.search(current->key[]);//r获取到p中 指向u的指针的序号
p->key.insert(r,current->key.remove(mid));//pivot关键码上升
p->child.insert(r+,right);
right->par=p; //新节点r与父节点p互联
solveOverFlow(p);//视角上升一层,有必要就继续分裂,最多递归O(logn)层,判断放在递归基里 }
下面说删除,把删除操作逆过来就行了,完结撒花。

虽然有相同之处,但还是有所区别的。关键在于删除之后可能内部节点里的关键码太少了,少于定义要求的下限,这时候我们称其为underflow,要做旋转与合并,不过这里的“旋转”并不是AVL的那种,下面我们就会看到这只是一种形象说法。以下先给出基本的算法框架,然后给出处理下溢的程序。
template <typename T>
bool BTree<T>::remove(const T & e){
Posi(T) target = search(e);
if(!target) return false;// 如果不存在,显然删除失败
Rank rk_e = target -> key.search(e); //在目标节点中获取到e的下标 if( target -> child[] ) { //确保不是叶子,那e的后继一定在某片叶子里
Posi(T) right = target -> child[rk_e+];//在右子树中一直向左即可
while ( right -> child[] )
right = right -> child[];//找出e的后继
target -> key[rk_e] = right -> key[];
target = right;
rk_e = ;// 交换target和e后继的位置
}//此时v到了底层,第r个元素就是要被删除的 target -> key.remove(rk_e); //删除e
target -> child.remove(rk_e+); //删除其中一个外部节点
_size--; //更新规模
solveUnderFlow(target);//如果有必要就旋转 or 合并
return true;
}
先明确一点,刚刚发生underflow的节点(叫做V),一定是恰好包含$\left\lceil \frac{M}{2} \right\rceil\; -\; 2$个关键码和$\left\lceil \frac{M}{2} \right\rceil\; -\; 1$条分支,也就是刚刚破坏了定义下界的情况。要分三种情况处理,分别是
- V的左兄弟存在,至少包含$\left\lceil \frac{M}{2} \right\rceil\; $个元素
- V的右兄弟存在,至少包含$\left\lceil \frac{M}{2} \right\rceil\; $个元素
- V兄弟不存在,或者包含的元素都不足$\left\lceil \frac{M}{2} \right\rceil\;$个
前两种情况是对称的,以1为例来着重讨论,就是下面这种情况

联想到在插入算法中通过分裂解决overflow,我们或许会首先想到通过合并来解决underflow。
不过这只是可供选择的预案之一,而不是上策。事实上我们首先会找这个节点的左右兄弟看看,借过来一个关键字,当然要保证这位兄弟别因此自己也下溢了。具体怎么借呢,一般会想到直接让x过来,这就可以了嘛。但是!B树也是搜索树,他也必须满足inorder条件下的单调递增性质,这就意味着作为左子树中的一员,L中的所有关键码都应该小于y,同样,作为右子树中的一员,V中的所有关键码都应该大于y。因此,将L中的任何一个关键码直接送到V中都会破坏这个顺序性,这也是接下来我们要迂回调度的原因所在。具体就是从父节点借一个y,再从L里给父节点补一个X,就保持收支平衡了。这个X一定要是L里面最大的元素,否则仍然会违背顺序性。
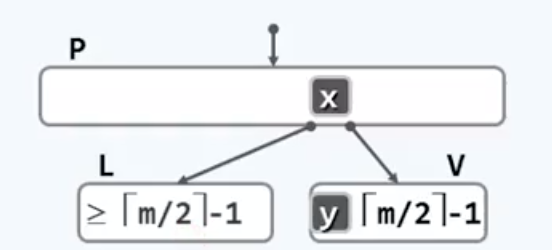
如此一来,经过两次调度,不仅解决了underflow问题,还保持了全局的顺序性。
2的情况如下,对称修复即可:
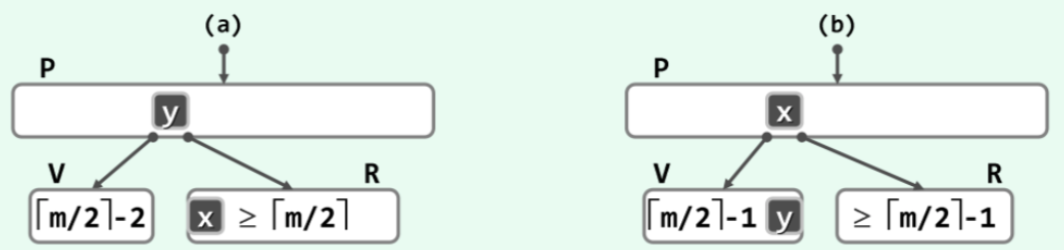
这是能旋转成的情况,那如果这时候发生underflow的节点没有兄弟节点,或者兄弟节点不足以借出时,又该如何呢?这时候才轮到合并操作上场,这也是我们需要考虑的最后一种情况。
第3种情况,我们必须心里有数,就算不足以借出,但是左右兄弟必然存在其一,不可能两个都不存在,这是一个如同三角形内角和180度的隐含条件。如图所示,此时是这种情形

仔细观察我们会发现,无论是V还是L的关键码数都很少,y只有一个,三者加起来也没有超过B树单个节点中关键码总数的上限$M-1$。顺着这个思路可以想到一个绝妙的办法:拼起来不就得了。就是从父节点中将这个分隔的关键码y取出来,以此为轴,把V和L两部分合并起来,使之成为一个新的节点。

尽管看起来很多,但是总体不超过$M-1$,仍然合法。这时候原先节点V所发生的下溢也在无形之中被消弭了,在此之后原先关键码y所对应的两个分支,也应该合并起来,指向这个新生成的大节点。不过这相当于从从父节点中删除了一个元素,可能使父节点发生underflow,那仍然可以转化为以上这三种情况之一,递归解决就行了,最多延伸到树根。这整个修复underflow的过程复杂度不会超过$O\left( h \right)$,这个结果还是令人肥肠满意的。
因为情况比较多,所以代码实现时要考虑的边边角角也很多。
template <typename T>
void BTree<T>::solveUnderFlow(Posi(T) v){
if( (_order + )>> <= v->child.size()) return; //当前节点没有发生下溢
Posi(T) p = v -> par;
if (!p) { //到达根节点
if (!v->key.size() && v -> child[]) { //如果v已经不含有关键码,但有唯一的非空child时
_root = v -> child[]; _root -> par = NULL;//这个节点被跳过
v -> child[] = NULL; delete v; //然后销毁
}//树高-1
return;
}
Rank r=;
while (p->child[r] !=v) r++; //确定v是p的第几个孩子,记作r //COND 1 向左借元素
if ( r > ) { //保证v不是p的第一个孩子
Posi(T) ls = p -> child[r-] ;//那左边一定有元素,是为左兄弟(left sibling),简称ls
if( (_order + )>> < ls->child.size() ){//如果这个兄弟家有余粮的话
v -> key.insert( , p -> key[r-] ); //v的父亲借出一个关键码作为v的min
p -> key[r-] = ls->key.remove( ls->key.size()- ); //ls的最大值补充给p
v -> child.insert( , ls->child.remove(ls->child.size() - ) );
if( v->child[] ) v->child[]->par =v;//最后两步调整对应的指针
return ; //右旋完成
}
} //至此左兄弟或者为空,或者不能再借了 // COND 2 向右借元素
if (p -> child.size() - > r ) { //如果v并非p的最后一个孩子
Posi(T) rs = p->child[r+]; //右边一定有元素
if ((_order + )>> < rs->child.size()) {
v -> key.insert( v->key.size() , p -> key[r] );
p -> key[r] = rs->key.remove();
v -> child.insert( v->child.size() , rs->child.remove() );
if( v->child[v->child.size()-] ) //v->child.size()-1是末尾下标
v->child[v->child.size()-]->par =v;//最后两步调整对应的指针
return; //左旋完成
}
}//至此右兄弟或者为空,或者不能再借了 // COND 3 需要合并
if ( < r) { //与左兄弟合并
Posi(T) ls = p -> child[r-];
ls->key.insert( ls -> key.size(), p -> key.remove(r-) );
// p的第r-1个关键码转入ls
ls->child.insert( ls -> child.size(),v -> child.remove());
if( ls->child[ ls->child.size() - ]) //把v最左边的孩子(min)给ls做最右侧孩子(max)
ls->child[ ls->child.size() - ] -> par = ls;
while (!v -> key.empty() ){ //若v中元素仍非空,就把剩余的依次转入ls
ls -> key.insert( ls -> key.size(), v->key.remove());
ls -> child.insert( ls -> child.size(), v->child.remove());
if( ls->child[ ls->child.size() - ] )
ls->child[ ls->child.size() - ] -> par =ls;
}
delete v; //合并后该局部的根已经空了,所以不妨将它删除,用合并后的节点作为新的根即可,下同
}
else{//与右兄弟合并
Posi(T) rs = p -> child[r+];
rs->key.insert( , p -> key.remove(r) );
p->child.remove(r); //以上两步将p的第r个关键码转入rs
rs->child.insert( ,v -> child.remove(v -> child.size() - ) );
if(rs -> child[] )
rs -> child[] -> par = rs;
while (!v -> key.empty()) { //若v中元素仍非空,就把剩余的依次转入rs
rs -> key.insert( , v->key.remove(v -> key.size()- ) );
rs -> child.insert( , v->child.remove( v -> child.size() - ) );
if( rs ->child[] )
rs->child[] -> par =rs;
}
delete v;
}
solveUnderFlow( p ); //继续检查上一层
return;
}
合并的例子比如:
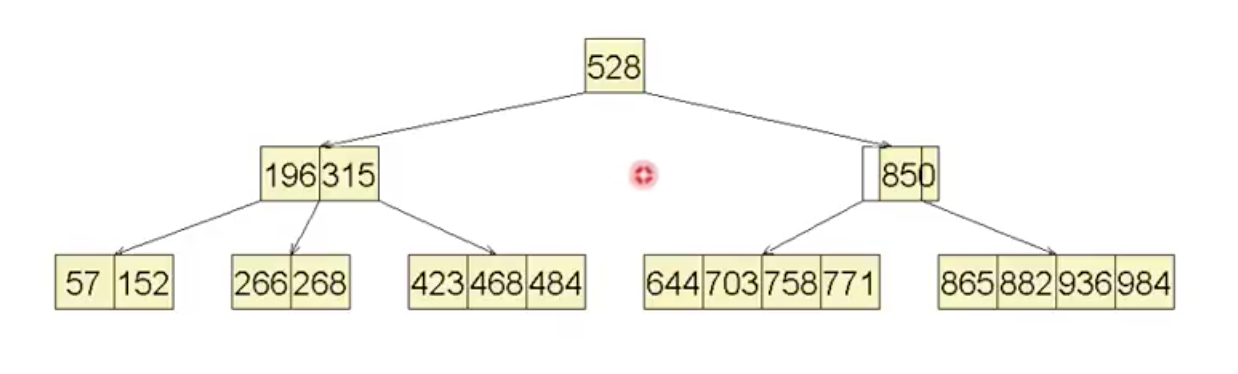
合并后如下:
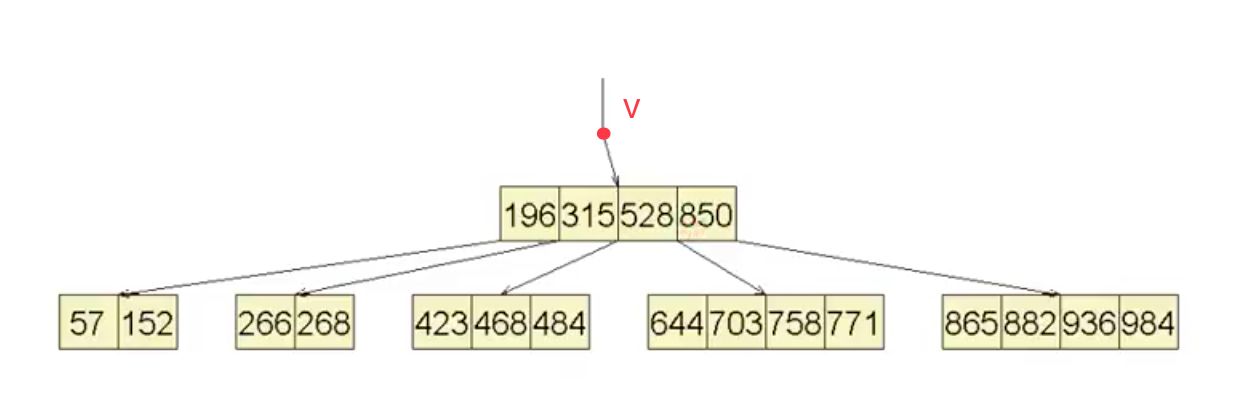
之所以要合并后delete v,是因为原先只包含唯一关键码的那个根节点现在却空了,在B树中 根节点拥有特权,可以只拥有两个分支,但不可能只拥有一个分支。这样一个根节点是没有任何实际用处的,所以我们不妨将它删除。合并操作引起的删除,也是B树高度得以下降的唯一可能。
回过头来看这幅图,B树被设计成这样又矮又宽的形状,是为了使外存操作的代价与内存操作的代价大致相当,因此B树可以通过适当调整自己的形态来适应IO操作和RAM访问之间的速度差异。
最新文章
- [LeetCode] Meeting Rooms 会议室
- 第3月第11天 vs2005调试 ace编译
- AFNetworking3.0介绍,收藏
- eclipse通过JDBC连接数据库不成功
- dll,lib文件的导入
- .net变量判断
- Datagrid扩展方法onClickCell{easyui-datagrid-扩充-支持单元格编辑}
- MySQL密码忘记之解决方法
- 交叉编译中的 --sysroot 等等在编译时的作用
- 调整altium designer15的十字光标大小
- sed删除空行和注释行
- java.util.zip.GZIPInputStream.readUByte,Not in GZIP format错误处理
- HDU 4616 Game (搜索)、(树形dp)
- 30第二建筑Github Page
- NSIS:在注册表中记录安装路径以便重装或升级时读取
- ftp服务搭建
- JavaScript:事件对象Event和冒泡
- SQL语句异常导致项目报错
- python实现一般最小二乘系统辨识方法
- 【BootStrap】 布局组件 I