Solution -「BZOJ3894」文理分科
Sol.
说实话,对于一个初学者,这道题很难看出是一道网络流-最小割。对于一个熟练者,这是比较套路的一种模型。
最小割,可以看做是在一个图中删掉最小的边权和使得源点、汇点不连通。或者换一个角度,可以看做是将图中的所有点以最小的代价分成两个阵营。
现在就有点像这道题了。我们以损失最小代价将这些学生分开为文理两阵营。
答案即为 \(\sum \limits _{i, j} \mathrm{Art}(i, j) + \sum \limits _{i, j} \mathrm{Science}(i, j) + \sum \limits _{i, j} \mathrm{SameArt}(i, j) + \sum \limits _{i, j} \mathrm{SameScience}(i, j) - d\)。
其中 \(d\) 就是我们要考虑的最小代价,可以根据上面的思路设想到它应该是一个流图的最小割。
研究以下这个图的一些限定条件,不妨设 \(S\) 为文阵营,即源点,\(T\) 为理阵营,即汇点。则有:
- 对于一个割,所有的图中表示人的结点应该与且仅与 \(S,T\) 中的一个连通。
- 当表示两个相邻的人的结点属于同一阵营时,一定有与它们属于另一阵营产生的额外价值等量的边(允许多条)属于割。
- 再发现,若一条边的边权为极值,则可以看做我们强制绑定了两点,且该边一定不出现在割中。
我很难描述具体构图时的思路。
大概是灵活运用极值边权,以及多考虑若一边属于割则会损失多少权值这样的小事件。
基础想法先是将 \(S\) 和一个人相连,边权为 \(\mathrm{Art}\),再将该人与 \(T\) 相连,边权为 \(\mathrm{Science}\)。
对于一个人即它相邻的人,我们考虑加入两个虚点,到 \(S, T\) 分别连 \(\mathrm{SameArt}, \mathrm{SameScience}\),再将这两个点和这五个人(当前人和相邻人)绑定。
也就是说如果这五人当中有一人与 \(S\) 连通,则连向 \(T\) 的虚点一定会断开。
如下图。(图源网络,侵删。
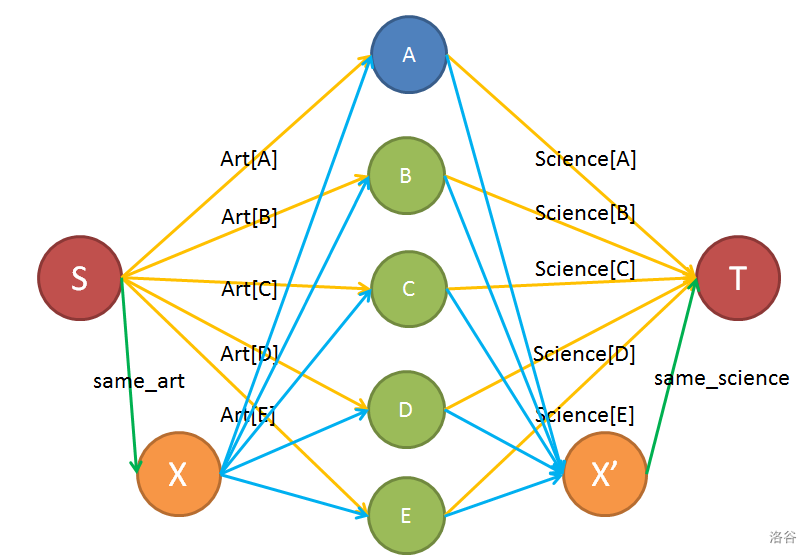
那么接下来就是一个最小割了。
Code.
#include <queue>
#include <cstdio>
using namespace std;
int Abs(int x) { return x < 0 ? -x : x; }
int Max(int x, int y) { return x > y ? x : y; }
int Min(int x, int y) { return x < y ? x : y; }
int read() {
int x = 0, k = 1;
char s = getchar();
while(s < '0' || s > '9') {
if(s == '-')
k = -1;
s = getchar();
}
while('0' <= s && s <= '9') {
x = (x << 3) + (x << 1) + (s ^ 48);
s = getchar();
}
return x * k;
}
void write(int x) {
if(x < 0) {
x = -x;
putchar('-');
}
if(x > 9)
write(x / 10);
putchar(x % 10 + '0');
}
void print(int x, char s) {
write(x);
putchar(s);
}
const int MAXN = 1e2 + 5;
const int MAXM = 1e5 + 4e4 + 5;
const int MAXL = 3e4 + 5;
const int INF = 2147483647;
struct Maximum_flow {
struct edge {
int v, nxt;
edge() {}
edge(int V, int Nxt) {
v = V, nxt = Nxt;
}
} e[MAXM << 1];
int n, cnt, s, t;
int Cap[MAXM << 1], Flow[MAXM << 1];
int Lab[MAXL], Cur[MAXL], head[MAXL];
queue<int> q;
void init(int N, int S, int T) {
for(int i = 0; i <= cnt; i++)
Flow[i] = 0, Cap[i] = 0;
n = N, cnt = 0, s = S, t = T;
for(int i = 1; i <= n; i++)
head[i] = -1;
}
void Add_Edge(int u, int v, int w) {
Cap[cnt] += w;
e[cnt] = edge(v, head[u]);
head[u] = cnt++;
e[cnt] = edge(u, head[v]);
head[v] = cnt++;
}
bool Lab_Vertex() {
for(int i = 1; i <= n; i++)
Lab[i] = 0;
Lab[t] = 1;
while(!q.empty())
q.pop();
q.push(t);
while(!q.empty()) {
int v = q.front();
q.pop();
for(int i = head[v], u; ~i; i = e[i].nxt) {
u = e[i].v;
if(!Lab[u] && Cap[i ^ 1] - Flow[i ^ 1]) {
Lab[u] = Lab[v] + 1;
q.push(u);
if(u == s)
return Lab[s];
}
}
}
return Lab[s];
}
int Widen(int u, int Limit) {
if(u == t)
return Limit;
int Used = 0, Delta;
for(int i = Cur[u], v; ~i; i = e[i].nxt) {
v = e[i].v;
Cur[u] = i;
if(Lab[v] + 1 != Lab[u] || Cap[i] - Flow[i] <= 0)
continue;
Delta = Widen(v, Min(Limit - Used, Cap[i] - Flow[i]));
Used += Delta, Flow[i] += Delta, Flow[i ^ 1] -= Delta;
if(Used == Limit)
return Used;
}
return Used;
}
int Dinic() {
int res = 0;
while(Lab_Vertex()) {
for(int i = 1; i <= n; i++)
Cur[i] = head[i];
res += Widen(s, INF);
if(res < 0)
return INF;
}
return res;
}
} Flow_Graph;
int dir[5][2] = {{0, 0}, {0, 1}, {1, 0}, {-1, 0}, {0, -1}};
int a[MAXN][MAXN][2], s[MAXN][MAXN][2], n, m;
int Get(int x, int y) { return (x - 1) * m + y; }
int main() {
n = read(), m = read();
int Sum = 0;
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
a[i][j][0] = read();
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
s[i][j][0] = read();
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
a[i][j][1] = read();
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
s[i][j][1] = read();
int S = n * m * 3 + 1, T = n * m * 3 + 2;
Flow_Graph.init(T, S, T);
for(int i = 1; i <= n; i++)
for(int j = 1, Pos; j <= m; j++) {
Pos = Get(i, j);
Sum += a[i][j][0], Sum += a[i][j][1], Sum += s[i][j][0], Sum += s[i][j][1];
Flow_Graph.Add_Edge(S, Pos, a[i][j][0]);
Flow_Graph.Add_Edge(Pos, T, s[i][j][0]);
Flow_Graph.Add_Edge(S, Pos + n * m, a[i][j][1]);
Flow_Graph.Add_Edge(Pos + n * m * 2, T, s[i][j][1]);
for(int k = 0, x, y; k < 5; k++) {
x = i + dir[k][0], y = j + dir[k][1];
if(x > n || x < 1 || y > m | y < 1)
continue;
Flow_Graph.Add_Edge(Pos + n * m, Get(x, y), INF);
Flow_Graph.Add_Edge(Get(x, y), Pos + n * m * 2, INF);
}
}
print(Sum - Flow_Graph.Dinic(), '\n');
return 0;
}
最新文章
- 在mysql 查询语句中将时间戳格式转化为年月日格式
- css文字两端对齐
- 問題排查:行動裝置網頁前端 UI 設計 (2)
- mysql 恢复备份时出错 Unknown command ‘\”
- Element.Event
- ios7学习之路七(隐藏虚拟键盘,解决键盘挡住UITextField问题)
- Python,datetime模块实例
- UWP更改标题栏颜色
- 【深度学习系列】用PaddlePaddle和Tensorflow实现经典CNN网络GoogLeNet
- 《蹭课神器》Beta版使用说明
- Oracle10.2.0.1以及其他版本升级Oracle10.2.0.5的简单步骤
- Java中的boxing和unboxing(转)
- python短域名数据分析框架
- ArcGIS模型构建器案例教程-批量复制工作空间所有要素类
- 【转发】JS中如何判断null/ undefined/IsNull
- Struts2初学 Struts2在Action获取内置对象request,session,application(即ServletContext)
- restframework api(基础1)
- [New learn] 设计模式
- vscode设置语言
- springmvc基础篇—通过注解的方式去配置项目
热门文章
- 【问题解决】'Access-Control-Allow-Origin' header contains multiple values '*, *', but only one is allowed.
- 【PyTorch】常用的神经网络层汇总(持续补充更新)
- 【Java分享客栈】SpringBoot线程池参数搜一堆资料还是不会配,我花一天测试换你此生明白。
- 在博客文章中使用mermaid 定义流程图,序列图,甘特图
- 溢出属性,定位,z-index,JS
- 在windows下使用s3cmd和s3browser来管理amazon s3的笔记
- python3在使用类基础时,遇到错误TypeError: module.**init**() takes at most 2 arguments (3 given)
- Simple, Fast Malicious Multiparty Private Set Intersection-解读
- docker的数据存储
- torch.tensor(),torch.Tensor()