Ⅱ Finite Markov Decision Processes

Dictum:

Is the true wisdom fortitude ambition. -- Napoleon

马尔可夫决策过程(Markov Decision Processes, MDPs)是一种对序列决策问题的解决工具，在这种问题中，决策者以序列方式与环境交互。

“智能体-环境”交互的过程

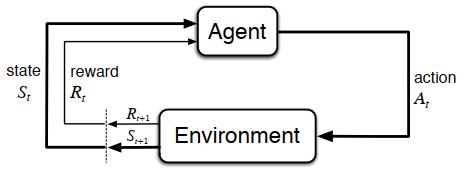
首先，将MDPs引入强化学习。我们可以将智能体和环境的交互过程看成关于离散情况下时间步长\(t(t=0,1,2,3,\ldots)\)的序列：\(S_0,A_0,R_1,S_1,A_1,R_2,S_2,A_2,R_3,\ldots\)，可以定义动作空间\(\mathcal{S}\)为所有动作的集合，定义状态空间\(\mathcal{A}\)为所有状态的集合。

马尔可夫决策过程

马尔可夫性

当且仅当状态满足下列条件，则该状态具有马尔科夫性

\[\mathbb{P}[S_{t+1}|S_t\ ]=\mathbb{P}[S_{t+1} |S_1,…,S_t] \tag{2.1}
\]

也就是说，未来状态只与当前状态有关，是独立于过去状态的。即当前状态捕获了所有历史状态的相关信息，是对未来状态的充分统计，因此只要当前状态已知，就历史状态就可以被丢弃。

动态特性

根据这个性质，我们可以写出状态转移概率\(\mathcal{P}_{ss^\prime}=\mathbb{P}[S_{t+1}=s^\prime\ |S_t=s]\)

由此可以得到状态转移矩阵\(\mathcal{P}\)：

\[\mathcal{P} = from
\begin{matrix}
to \\
\left[\begin{array}{rr}
\mathcal{P}_{11} & \cdots & \mathcal{P}_{1n} \\
\vdots & \ddots & \vdots \\
\mathcal{P}_{n1} & \cdots & \mathcal{P}_{nn} \\
\end{array}\right]
\end{matrix} \tag{2.2}
\]

(该矩阵中所有元素之和为1)

我们将函数\(p\)定义为MDP的动态特性，通常情况下\(p\)是一个包含四个参数的确定函数(\(p: \mathcal{S}\times\mathcal{A}\times\mathcal{S}\times\mathcal{R}\rightarrow[0,1]\))：

\[p(s^\prime,r|s,a)\doteq\Pr\{S_t=s^\prime,R_t=r|S_{t-1}=s,A_{t-1}=a\} \tag{2.3}
\]

或者，我们可以定义一个三个参数的状态转移概率\(p\)(\(p: \mathcal{S}\times\mathcal{S}\times\mathcal{A}\rightarrow[0,1]\))：

\[p(s^\prime|s,a)\doteq\Pr\{S_t=s^\prime|S_{t-1}=s,A_{t-1}=a\}= \sum_{r \in \mathcal{R}}p(s^\prime,r|s,a) \tag{2.4}
\]

由此，可以定义“状态-动作”二元组的期望奖励\(r(r:\mathcal{S}\times\mathcal{A}\rightarrow\mathbb{R})\)：

\[r(s,a)\doteq\mathbb{E}[R_t|S_{t-1}=s,A_{t-1}=a]=\sum_{r\in\mathcal{R}}r\sum_{s^\prime\in\mathcal{S}}p(s^\prime,r|s,a) \tag{2.5}
\]

也可以定义“状态-动作-后继状态”三元组的期望奖励\(r(r:\mathcal{S}\times\mathcal{A}\times\mathcal{S}\rightarrow\mathbb{R})\)：

\[r(s,a,s^\prime)\doteq\mathbb{E}[R_t|S_{t-1}=s,A_{t-1}=a,S_t=s^\prime]=\sum_{r\in\mathcal{R}}r\frac{p(s^\prime,r|s,a)}{p(s^\prime|s,a)} \tag{2.6}
\]

价值函数

回报

回报(Return)的定义式为

\[G_t\doteq\displaystyle \sum^{T}_{k=t+1}\gamma^{k-t-1}R_k,\ 0\le\gamma \le 1 \tag{2.7}
\]

\(\gamma\)被称为折扣率(discount rate)。当\(T= \infin\)且\(0 \le \gamma<1\)时，强化学习任务被称为连续任务(continuing tasks)，当\(\gamma=1\)且\(T\ne\infin\)时，强化学习任务被称为幕式任务(episodic tasks)。

episodic tasks的智能体和环境的交互过程能够被拆分为一系列的子序列。在这类任务中，当时间步长\(t\)达到某个值\(T\)时，会产生终止状态(terminal state)。这种状态下，对于任意\(k>1,S_{T+k}=S_T=s\)恒成立，此时，\(T\)被称为终止时刻，它随着幕(episode)的变化而变化。从起始状态到达终止状态的每个子序列被称为幕。

策略

策略(Policy)\(\pi\)是状态到动作空间分布的映射

\[\pi(a|s)= \mathbb{P}[A_t=a|S_t=s] \tag{2.8}
\]

它表示根据当前状态\(s\)，执行动作\(a\)的概率。

状态价值函数

状态价值函数(State-value Function)\(v_\pi(s)\)定义为从状态\(s\)开始，执行策略\(\pi\)所获得的回报的期望值。

\[v_\pi(s) \doteq \mathbb{E}_\pi[G_t|S_t=s]=\mathbb{E}[\sum^\infin_{k=0} \gamma^kR_{t+k+1}|S_t=s], s \in \mathcal{S} \tag{2.9}
\]

动作价值函数

类似于公式\((2.9)\)的定义，将动作价值函数(Action-value Function)\(q_\pi(s,a)\)定义为在状态\(s\)时采取动作\(a\)后，所有可能的决策序列的期望回报。

\[q_\pi(s,a) \doteq \mathbb{E}_\pi[G_t|S_t=s，A_t=a]=\mathbb{E}[\sum^\infin_{k=0} \gamma^kR_{t+k+1}|S_t=s，A_t=a], s \in \mathcal{S} \tag{2.10}
\]

贝尔曼方程

贝尔曼方程(Bellman Euqation)是以等式的方式表示某一时刻价值与期后继时刻价值之间的递推关系。

下面给出状态价值函数\(v_\pi(s)\)的贝尔曼方程：

\[\begin{aligned}
v_\pi(s)
& \doteq \mathbb{E}_\pi[G_t|S_t=s] \\
& =\mathbb{E}_\pi[R_{t+1}+ \gamma G_{t+1}|S_t=s] \\
& =\displaystyle \sum_a\pi(a|s) \sum_{s^\prime} \sum_rp(s^\prime,r|s,a)[r+\gamma \mathbb{E}_\pi[G_{t+1}|S_{t+1}=s^\prime]] \\
& =\displaystyle \sum_a\pi(a|s) \sum_{s^\prime.r} p(s^\prime,r|s,a) [r+\gamma v_\pi(s^\prime)]
\end{aligned} \tag{2.11}
\]

可以通过下面关于\(v_\pi(s)\)的回溯图(backup diagram)更好地理解上述方程，backup就是将价值信息从后继状态（或“状态-动作”二元组）转移到当前状态（或“状态-动作”二元组）。

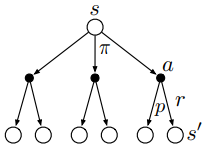
在上图中，由上往下看，空心圆表示状态，实心圆表示“状态-动作”二元组。图中，从根节点状态\(s\)开始，智能体根据策略\(\pi\)采取动作集合中的任意动作，对于每个动作，环境会根据它的动态特性函数\(p\)，给出奖励值\(r\)和后继状态\(s^\prime\)。

同样也可以通过\(q_\pi\)的回溯图得到它的贝尔曼方程（同时也给出推导过程）：

\[\begin{aligned}
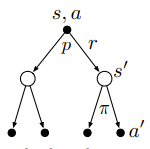
q_\pi(s,a)
& \doteq \mathbb{E}_\pi[G_t|S_t=s,A_t=a] \\
& =\mathbb{E}_\pi[R_{t+1}|S_t=s,A_t=a]+ \gamma \mathbb{E}_\pi[G_{t+1}|S_t=s,A_t=a] \\
& =\displaystyle \sum_{s^\prime,r}p(s^\prime,r|s,a)r+ \gamma \sum_{s^\prime,r}p(s^\prime,r|s,a) \sum_{a^\prime}\pi(a^\prime|s^\prime) \mathbb{E}_\pi[G_{t+1}|S_{t+1}=s^\prime,A_{t+1}=a^\prime] \\
& =\displaystyle \sum_{s^\prime,r}p(s^\prime,r|s,a)[r+ \gamma \sum_{a^\prime}\pi(a^\prime|s^\prime)q_\pi(s^\prime,a^\prime)]
\end{aligned} \tag{2.12}
\]

价值函数的相互转换

从定义的角度，我们更容易理解\(v_\pi(s)\)和\(q_\pi(s,a)\)的关系。我们可以将\(q_\pi(s,a)\)理解为执行策略后选取动作空间中一个动作所得到的价值函数，而将\(v_\pi(s)\)理解为执行策略后选择动作空间中所有动作所得到的价值函数。\(v_\pi\)其实就是\(q_\pi\)基于策略\(\pi\)的期望值，所以它们的关系转换如下：

\[v_\pi(s)= \sum_a \pi(a|s)q_\pi(s,a) \tag{2.13}
\]

它的回溯图如下图所示：

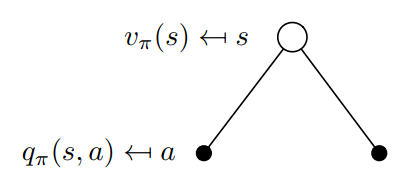
也可以按照下面的回溯图写出状态价值函数到动作价值函数的转换：

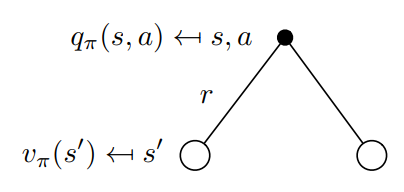
\[q_\pi(s,a) =\displaystyle \sum_{s^\prime,r}[r+ \gamma v_\pi(s^\prime)] \tag{2.14}
\]

最优策略和最优价值函数

最优策略

智能体的目标就是找出一种策略，能够最大化它的长期奖励，这个策略就是最优策略(optimal policy)，记作\(\pi_*\)。公式表示如下：

\[\forall s \in \mathcal{S}, \exist \pi_* \ge \pi, v_{\pi_*}(s) \ge v_\pi(s) \tag{2.15}
\]

也可以将上式的状态价值函数替换为动作价值函数，它们在寻找最优策略上是等价的。

最优价值函数

最优状态价值函数可以定义为

\[v_*(s) \doteq \max_\pi v_\pi(s) \tag{2.16}
\]

\(v_*(s)\)的贝尔曼最优方程为

\[v_*(s)=\displaystyle \max_a \sum_{s^\prime.r} p(s^\prime,r|s,a) [r+\gamma v_*(s^\prime)] \tag{2.17}
\]

最优动作价值函数可以定义为

\[q_*(s,a) \doteq \max_\pi q_\pi(s,a) \tag{2.18}
\]

\(q_*(s,a)\)的贝尔曼最优方程为

\[q_*(s,a)=\displaystyle \sum_{s^\prime,r}p(s^\prime,r|s,a)[r+ \gamma \max_{a^\prime} q_*(s^\prime,a^\prime)] \tag{2.19}
\]

下图展示了\(v_*(s)\)和\(q_*(s,a)\)的贝尔曼最优方程的回溯图（弧线表示在给定策略下取最大值而不是期望值）

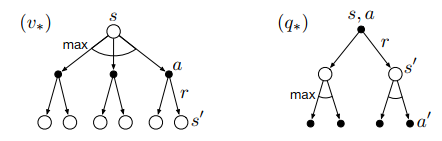
后续概念

强化学习的方法

强化学习方法可以分为基于模型的(model-based)和不基于模型的(model-free)，二者之间的区别在于是否有完备的环境知识，若存在MDP中的状态转移概率矩阵\(\mathcal{P}\)，且能得到相应的奖励\(\mathcal{R}\)，则是基于模型的；否则，是不基于模型的。

强化学习的问题

一般来说，强化学习问题可以分为两步：一、预测问题——给定强化学习的相关要素，评估价值函数；二、控制问题——求解最优价值函数和最优策略。

FAQ

Q：如果当前状态是\(S_t\)，并根据随机策略\(\pi\)选择动作，那么如何用\(\pi\)和四参数\(p\)表示\(R_{t+1}\)的期望？

A：\(\mathbb{E}_\pi[R_{t+1}|S_t=s]=\displaystyle \sum_a\pi(a|s) \sum_{s^\prime,r}rp(s^\prime,r|s,a)\)

References

Richard S. Sutton and Andrew G. Barto. Reinforcement Learning: An Introduction (Second Edition). 2018.

Csaba Szepesvári. Algorithms for Reinforcement Learning. 2009.

Course: UCL Reinforcement Learning Course (by David Silver)

巴特西