NOIP2018 Day2T2 填数游戏

下面先给出大家都用的打表大法：

首先我们可以发现 \(n \le 3\) 的情况有 \(65pts\)，而 \(n\) 这么小，打一下表何乐而不为呢？于是我写了一个爆枚每个位置再 \(check\) 的 \(dfs\)，复杂度 \(O(2 ^ {nm + n + m} \log 2 ^ {n + m - 1})\) 因为 \(n\) 实在太小了于是我打出了下面的表（\(1\) 的情况直接算就没打了，下面第一个数都是从 \(m = n\) 开始的）

2 : 12 36 108 324 ...

3 : 112 336 1008 3024 ...

很明显可以发现这里每个答案往后都乘了 \(3\)，于是我们只需要写一个快速幂就可以获得 \(65pts\) 的高分。之后我算出了 \((4, 4)\) 的答案 \(912\)，又算了 \((4, 5)\) 的答案想要验证乘 \(3\) 的猜想，但 \((4, 5)\) 却是 \(2688 \ne 3 \times 912\)，然后我再想跑出 \((4, 6)\) 的答案，可是目前的 \(dfs\) 大概要跑 \(2h\) 左右，于是我再分析了一下样例，发现实际上题目的要求是优先往右走的路径的 \(01\) 字典序要不大于优先往下走的所有路径 \(01\) 字典序，因此我有了这样一个剪枝方法，我们先暴力枚举第一列的所有数，然后从最后一行开始暴力枚举，吧每一条路径压乘十进制数在树状数组上修改，那么再一遍遍爆枚上一层，记录一下每个位置到终点的最大 \(01\) 字典序加到当前的字典序后面然后再在线段树上查询是否有小于当前字典序的串，如果有剪枝即可。这个东西看起来很难实现，而且复杂度也很玄学，回头想一下题目的条件，要求优先往右走的字典序小，那么假设现在有两个 \(01\) 串 \(a, b\) 前者优先往下走，后者优先往右走，假设目前两串相同，如果下面 \(a < b\) 那么后者必然走到 \(1\) 而前者必然走到 \(0\)，再注意到 \(a, b\) 长度应该相等也就意味着两者走的步数相同，那么两者应该都在左下到右上的一条对角线上，因此我们可以得出一个结论，每一条左下到右上的对角线都是先一段 \(1\) 后一段 \(0\)。那么我们就可以有了一种新的爆搜方式，我们爆枚每个对角线 \(0, 1\) 分界点，再暴力 \(check\) 这样复杂度是 \(O((m!) ^ 2 2 ^ {n + m} \log 2 ^ {n + m})\)，算了一下这东西能跑出 \((6, 6)\)，于是我实现了这个 \(dfs\)，发现 \((6, 6)\) 只需要 \(15s\)，于是我让他去跑 \((7, 7)\) 打出了 \(n \le 6\) 的表。

2 : 12 36 108 324 972 2916 ...

3 : 112 336 1008 3024 9072 27216 ...

4 : 912 2688 8064 24192 72576 217728 ...

5 : 7136 21312 63936 191808 ...

6 : 56768 170112 510336 ...

可以发现，虽然 \((4, 4) \rightarrow (4, 5)\) 不是乘 \(3\)，但 \((4, 5) \rightarrow (4, 6), (4, 6) \rightarrow (4, 7)\) 接下来都是乘 \(3\)，对于 \(5, 6\) 也是一样。于是我们大胆地猜测剩下的所有情况应该都是从第二项开始乘 \(3\) 的。那我们只需要求出第一项和第二项即可。

过了 \(20min\) 终于跑出了 \((7, 7)\)，现在的表如下：

2 : 12 36 108 324 972 2916 ...

3 : 112 336 1008 3024 9072 27216 ...

4 : 912 2688 8064 24192 72576 217728 ...

5 : 7136 21312 63936 191808 ...

6 : 56768 170112 510336 ...

7 : 453504 ...

感觉 \((7, 8)\) 应该是死都跑不出来了，但是我们打表出了这么多数据，可以找一下规律。我们发现 \(n \ge 4\) 时虽然第一项乘 \(3\) 不等于第二项，但隔得非常近，于是我算出了 \(n = 4\) 时 \(912 \times 3 - 2688 = 48\)，接着再算了 \(n = 5\) 时 \(7136 \times 3 - 21312 = 96\)，然后又算了 \(n = 6\) 时 \(56768 \times 3 - 170112 = 192\)，规律非常明显了，每次插值乘了 \(2\)，并且可以发现 \(48 = 3 \times 2 ^ 4, 96 = 3 \times 2 ^ 5\)，于是我们可以发现 \((n, n + 1) = 3 \times (n, n) - 3 \times 2 ^ n\)，那么我们只需要跑出 \((8, 8)\) 这题就做完了，然而貌似 \((8, 8)\) 根本跑不出...

应该还有规律，继续观察。可以发现 \(m \ge n + 2\) 的情况都是从 \((n, n + 1)\) 推来的，而 \((n, n + 1)\) 与 \((n, n)\) 有关，于是我们可以考虑只观察前面两项，观察一段时间后可以发现 \(((n, n) + (n, n + 1)) \times 2\) 与 \((n + 1, n + 1)\) 非常接近，于是我又算了他们的差值可以发现 \(4 \rightarrow 5 = 64, 5 \rightarrow 6 = 128, 6 \rightarrow 7 = 256\)，规律也非常明显，每次乘了 \(2\)，并且可以发现每次的插值 \(i - 1 \rightarrow i = 2 ^ {i + 1}\)，那么我们岂不是知道前两项的递推式了？令 \(f_{i, j}\) 为 \((i, j)\) 的答案，于是我们有 \(f_{i, i} = (f_{i - 1, i - 1} + f_{i - 1, i}) \times 2 - 2 ^ {i + 1}, f_{i, i + 1} = 3 \times f_{i, i} - 3 \times 2 ^ i\)，于是我们直接矩阵快速幂递推出前两项，后面的直接使用快速幂即可。

#include<bits/stdc++.h>

using namespace std;

#define N 5

#define Mod 1000000007

#define rep(i, l, r) for(int i = l; i <= r; ++i)

struct mat{

    int g[N][N];

    void clear(){ memset(g, 0, sizeof(g));}

}f, tr, ans;

int n, x, m;

int read(){

    char c; int x = 0, f = 1;

    c = getchar();

    while(c > '9' || c < '0'){ if(c == '-') f = -1; c = getchar();}

    while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();

    return x * f;

}

int Inc(int a, int b){

    return (a += b) >= Mod ? a - Mod : a;

}

int Dec(int a, int b){

    return (a -= b) < 0 ? a + Mod : a;

}

int Mul(int a, int b){

    return 1ll * a * b % Mod;

}

int Qpow(int a, int b){

    int ans = 1;

    while(b){

        if(b & 1) ans = Mul(ans, a);

        a = Mul(a, a), b >>= 1;

    }

    return ans;

}

mat mul(mat a, mat b){

    mat c; c.clear();

    rep(i, 1, 3) rep(j, 1, 3) rep(k, 1, 3) c.g[i][j] = Inc(c.g[i][j], Mul(a.g[i][k], b.g[k][j]));

    return c;

}

int main(){

    n = read(), m = read(); if(n > m) swap(n, m);

    if(n == 1) printf("%d", Qpow(2, m));

    else if(n == 2) printf("%d", Mul(12, Qpow(3, m - 2)));

    else if(n == 3) printf("%d", Mul(112, Qpow(3, m - 3)));

    else{

        f.g[1][1] = 912, f.g[1][2] = 2688, f.g[1][3] = 32;

        tr.g[1][1] = 2, tr.g[1][2] = 6, tr.g[1][3] = 0;

        tr.g[2][1] = 2, tr.g[2][2] = 6, tr.g[2][3] = 0;

        tr.g[3][1] = Mod - 2, tr.g[3][2] = Mod - 9, tr.g[3][3] = 2;

        ans.g[1][1] = ans.g[2][2] = ans.g[3][3] = 1;

        x = n - 4;

        while(x){

            if(x & 1) ans = mul(ans, tr);

            tr = mul(tr, tr), x >>= 1;

        }

        f = mul(f, ans);

        if(n == m) printf("%d", f.g[1][1]);

        else printf("%d", Mul(f.g[1][2], Qpow(3, m - n - 1)));

    }

    return 0;

}

我们可以继续按照计数的套路考虑怎样的一个矩阵是合法的，我们之前已经发现了一个条件：所有对角线（下面默认从左下到右上）一定都是 \(111 \cdots 0000\) 排列，但是我们需要注意的是这是两条路径没有相交的情况，那么如果两条路径相交，接下来下和右的优先级实际上反了过来，那么剩下的子矩阵所有对角线都将会是 \(000 \cdots 1111\) 这样子的，因此剩下的子矩阵的所有对角线要么全为 \(0\) 要么全为 \(1\)，于此同时如果两条路径能在某个点相交当且仅当这个点上面的点和左边的点权值相同，因此一张合法矩阵的充要条件如下：

\(1.\) 所有对角线都是先一段 \(1\) 再一段 \(0\).

\(2.\) 对于所有的 \(x, y, a_{x - 1, y} = a_{x, y - 1}\)，满足 \((x, y)\) 为左上角 \((n, m)\) 为右上角的矩形中所有对角线的权值相同。

于是我们可以考虑如何快速判断一个矩形是否合法，首先我们每次枚举一定是满足第一个条件的，只需要考虑第二个条件即可，我们当然可以枚举每个点，然后暴力判断对角线，但这样是不优的，不难发现如果我们令 \(dp_{i, j}\) 为 \((i, j) \sim (n, m)\) 这个矩形是否合法，那么就会有转移 \(dp_{i, j} = dp_{i + 1, j} \& dp_{i, j + 1} \& (a_{i, k} = a_{i + 1, k - 1} (j + 1 \le k \le m))\)，最右边的那个东西是可以提前预处理出来的，于是判断我们就能 \(O(nm)\) 做了，于是直接考虑从最后一个对角线往前填，沿途一路 \(check\) 过来，这样的复杂度就很优了，跑出 \((8, 8)\) 轻而易举。有了上面这个判定方法以后实际上我们可以直接状压，令 \(dp_{i, j, k}\) 为当前枚举到第 \(i\) 个对角线，当前放置了 \(j\) 个 \(1\)，强制对角线相同的位置状态为 \(k\) 的方案数，暴力转移即可，复杂度 \(O(n ^ 3 m 2 ^ n)\) 有很多转移是可以省去的，这样这个 \(dp\) 就可以跑得飞快了，我们可以轻松地打出大量的表那么也就可以轻松发现规律了，因此如果这个题想到这里实际上已经做完了本题，但本题还有更巧妙的性质没有发现。

我们考虑第 \(3\) 条对角线，不难发现这一条对角线上一定存在两个相同的相邻的权值，那么我们就能约数掉大部分的情况了，首先我们可以证明一下上面打表得出的 \(f_{n, m} = 3 \times f_{n, m - 1}\) 的结论。（感谢 \(\rm xenonex\) 的图）

分几种情况讨论一下，如果第二条对角线两个权值相同：

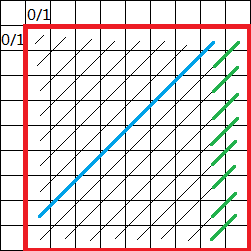
首先红框内是受限制的矩形，可以考虑新增加一列来计算增加的贡献，假设现在新增加最后绿色所在一列，不难发现有部分会随着之前矩形而受限制（绿色部分）而右下角的那个格子可以随意选择 \(0 / 1\)，而右上角的那个位置会受蓝色对角线的影响，蓝色对角线有 \(\frac{1}{2}\) 的情况都选择 \(0\)，那么右上角一定也会选择 \(0\)，有 \(\frac{1}{2}\) 的情况选择 \(1\)，那么右上角可以随意选择 \(0 / 1\)，因此这部分的增量为 \(2 \times \frac{1}{2} (1 + 2) = 3\)。

剩下的情况只需枚举第三条对角线的所有状态，证明方法和上面的证明方法类似。

实际上上面的证明方法也给了我们很好的做题思路，我们同样可以分类讨论算出答案。

第二条对角线两个权值相同：

第一条第二条对角线都有两种选择，从第三条对角线开始，因为框内选数被限制，对于小于 \(n\) 的每条对角线可以看作是三个点的对角线需要满足第一个条件，不难发现有 \(4\) 种填法，而对于大于 \(n\) 小于等于 \(m\) 的每条对角线均有 \(3\) 种填法，剩下的情况只有两种填法，第一条对角线和第二条对角线分别有 \(2\) 种填法，因此此部分答案为 \(2 \times 2 \times 4 ^ {n - 2} \times 3 ^ {m - n} \times 2 ^ {n - 1} = 2 ^ {3n - 3} \times 3 ^ {m - n}\)

第二条对角线两个权值不相同且第三条对角线三个权值相同：

和上面的情况同理，答案为 \(5 \times 4 ^ {n - 4} \times 3 ^ {m - n} \times 2 ^ {n - 1} = 2 ^ {3n - 9} \times 3 ^ {m - n} \times 5\).

第二条对角线两个权值不相同且第三条对角线为 \(1, 1, 0\)

不难发现这里统计答案的难点在于上方 \(2 \times m\) 的一个矩形，因为如果不约束这个矩形答案非常难统计，可以考虑令 \(dp_{i, 0 / 1}\) 为当前选到第 \(i\) 条对角线，当前上方的矩形有没有被约束的方案，于是就有转移

\[dp_{i, 0} = dp_{i - 1, 0}
\]

\[dp_{i, 1} = dp_{i - 1, 0} \times 4 + dp_{i - 2, 0} \times 4 \times 5 + (dp_{i - 1, 1} - dp_{i - 2, 0} \times 4) \times 4 = 4 \times (dp_{i - 1, 0} + dp_{i - 1, 1} + dp_{i - 2, 0})(i \le n)
\]

\[dp_{i, 1} = 3 \times dp_{i - 1, 0} + 4 \times dp_{i - 2, 0} \times 4 + (dp_{i - 1, 1} - 4 \times dp_{i - 2, 0}) \times 3 = 3 \times (dp_{i - 1, 0} + dp_{i - 1, 1}) + 4 \times dp_{i - 2, 0}(i = n + 1)
\]

\[dp_{i, 1} = 3 \times dp_{i - 1, 0} + 3 \times dp_{i - 2, 0} \times 4 + (dp_{i - 1, 1} - 3 \times dp_{i - 2, 0}) \times 3 = 3 \times (dp_{i - 1, 0} + dp_{i - 1, 1} + dp_{i - 2, 0})(i \le m)
\]

那么最终答案如下：

\[(3 \times dp_{m, 0} + 12 \times dp_{m - 1, 0} + 2 \times (dp_{m, 1} - 4 \times dp_{m - 1, 0})) \times 2 ^ {n - 1} = (3 \times dp_{m, 0} + 2 \times dp_{m, 1} - 4 \times dp_{m - 1, 0}) \times 2 ^ {n - 1}(m \le n)
\]

\[(3 \times dp_{m, 0} + 9 \times dp_{m - 1, 0} + 2 \times (dp_{m, 1} - 3 \times dp_{m - 1, 0})) \times 2 ^ {n - 1} = (3 \times dp_{m, 0} + 2 \times dp_{m, 1} - 3 \times dp_{m - 1, 0}) \times 2 ^ {n - 1}(m \le n)
\]

第二条对角线两个权值不相同且第三条对角线为 \(1, 0, 0\)

与上面的情况类似

最终可以使用矩阵快速幂即可做到 \(O(\log n + \log m)\).

#include<bits/stdc++.h>

using namespace std;

#define N 2000000 + 5

#define Mod 1000000007

#define rep(i, l, r) for(int i = l; i <= r; ++i)

int n, m, ans, tmp, dp[N][2];

int read(){

	char c; int x = 0, f = 1;

	c = getchar();

	while(c > '9' || c < '0'){ if(c == '-') f = -1; c = getchar();}

	while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();

	return x * f;

}

int Inc(int a, int b){

	return (a += b) >= Mod ? a - Mod : a;

}

int Dec(int a, int b){

	return (a -= b) < 0 ? a + Mod : a;

}

int Mul(int a, int b){

	return 1ll * a * b % Mod;

}

int Qpow(int a, int b){

	int ans = 1;

	while(b){

		if(b & 1) ans = Mul(ans, a);

		a = Mul(a, a), b >>= 1;

	}

	return ans;

}

int main(){

	n = read(), m = read(); if(n > m) swap(n, m);

	if(n == 1) printf("%d", Qpow(2, m));

	else if(n == 2) printf("%d", Mul(12, Qpow(3, m - 2)));

	else if(n == 3) printf("%d", Mul(112, Qpow(3, m - 3)));

	else{

		ans = Mul(Qpow(2, 3 * n - 3), Qpow(3, m - n));

		ans = Inc(ans, Mul(Mul(Qpow(2, 3 * n - 9), Qpow(3, m - n)), 20));

		dp[3][0] = 1;

		rep(i, 4, m){

			dp[i][0] = dp[i - 1][0];

			if(i <= n) dp[i][1] = Mul(4, Inc(dp[i - 1][0], Inc(dp[i - 1][1], dp[i - 2][0])));

			else{

				dp[i][1] = Mul(3, Inc(dp[i - 1][0], dp[i - 1][1]));

				if(i - 1 <= n) dp[i][1] = Inc(dp[i][1], Mul(4, dp[i - 2][0]));

				else dp[i][1] = Inc(dp[i][1], Mul(dp[i - 2][0], 3));

			}

		}

		tmp = Mul(3, dp[m][0]);

		if(m <= n){

			tmp = Inc(tmp, Mul(dp[m - 1][0], 12));

			tmp = Inc(tmp, Mul(Dec(dp[m][1], Mul(dp[m - 1][0], 4)), 2));

		}

		else{

			tmp = Inc(tmp, Mul(dp[m - 1][0], 9));

			tmp = Inc(tmp, Mul(Dec(dp[m][1], Mul(dp[m - 1][0], 3)), 2));

		}

		if(m <= n){

			tmp = Mul(tmp, Qpow(2, n));

			ans = Inc(ans, tmp);

			printf("%d", ans);

			return 0;

		}

		tmp = Mul(tmp, Qpow(2, n - 1));

		ans = Inc(ans, tmp);

		memset(dp, 0, sizeof(dp));

		dp[3][0] = 1;

		rep(i, 4, n){

			dp[i][0] = dp[i - 1][0];

			dp[i][1] = Mul(4, Inc(dp[i - 1][0], Inc(dp[i - 1][1], dp[i - 2][0])));

		}

		tmp = Mul(4, dp[n][0]);

		tmp = Inc(tmp, Mul(dp[n - 1][0], 16));

		tmp = Inc(tmp, Mul(Dec(dp[n][1], Mul(dp[n - 1][0], 4)), 3));

		tmp = Mul(tmp, Qpow(3, m - n - 1));

		tmp = Mul(tmp, Qpow(2, n));

		ans = Inc(ans, tmp);

		printf("%d", ans);

	}

	return 0;

}

巴特西

NOIP2018 Day2T2 填数游戏

最新文章

热门文章