CRT中国剩余定理 & Lucas卢卡斯定理

数论_CRT（中国剩余定理）& Lucas （卢卡斯定理）

前言

又是一脸懵逼的一天。

正文

按照道理来说，我们应该先做一个介绍。

中国剩余定理

中国剩余定理，Chinese Remainder Theorem，又称孙子定理，给出了一元线性同余方程组的有解判定条件，并用构造法给出了通解的具体形式。

现在有方程组：中国剩余定理指出：

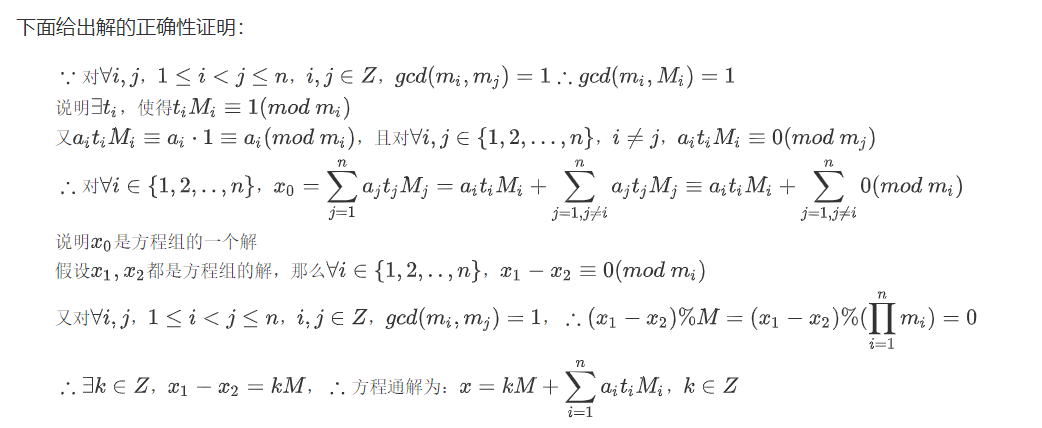
扩展中国剩余定理

在一般情况下，要求任两个数互质这个条件太苛刻了，CRT派不上用场，我们需要一个更具普遍性的结论，这就是EX-CRT。虽然是称为EX-CRT，但这个定理并没有直接用到CRT的结论。

typedef long long ll;
const int maxn = 111;

// m为模数组，a为余数数组，0~n-1
ll m[maxn], a[maxn];

ll exgcd(ll a, ll b, ll &x, ll &y) {
    if (b == 0) {
        x = 1; y = 0;
        return a;
    }
    ll ans = exgcd(b, a % b, y, x);
    y -= a / b * x;
    return ans;
}

ll excrt() {
    ll lcm = m[0], last_a = a[0];
    for(int i = 1; i < n; i++) {
        ll lcm_a = ((a[i] - last_a) % m[i] + m[i]) % m[i];
        ll k = lcm, x, y;
        ll gcd = exgcd(lcm, m[i], x, y);
        ll mod = m[i] / gcd;
        x = (x * lcm_a / gcd % mod + mod) % mod;
        lcm = lcm / gcd * m[i], last_a = (last_a + k * x) % lcm;
    }
    return (last_a % lcm + lcm) % lcm;
}

卢卡斯定理

卢卡斯定理是关于组合数和同余的定理，它表明当p为素数时：

其中，即为的进制展开中对应次数为的系数

因为当m>n时，二项式系数为0，那么二项式系数即组合数能被p整除等价于在p进制下，存在某一位m的数值大于对应的n的数值。

基于母函数可以简单证明这个定理。

可以用除法和取模方便的在循环中求出各个系数，代码如下：

typedef long long ll;
const int mod = 1e9 + 7;
const int maxn = 1e5 + 100;

void init() {
    F[0] = 1;
    for(int i = 2; i < maxn; i++)
        F[i] = i * F[i - 1] % mod;
}

ll qpow(ll a, ll b) {
    ll ans = 1;
    while(b) {
        if(b & 1) ans = ans * a % mod;
        b >>= 1; a = a * a % mod;
    }
    return ans;
}

ll lucas(ll N, ll M) {
    ll ans = 1;
    while(N & M) {
        ll n = N % mod, m = M % mod;
        if(n < m) return 0;
        ans = ans * F[a] % mod * qpow(F[m] * F[n - m] % mod, mod - 2) % mod;
        N /= p; M /= p;
    }
    return ans;
}

扩展卢卡斯定理

卢卡斯定理同样不能处理模数不是素数的情况，这时便需要扩展卢卡斯定理。我们一步步分析如何求解模数不是素数的组合数问题。

首先，我们要解决的问题是求，其中不一定是素数。对于非素数，我们首先会联想到质因分解后结合解决问题。假设分解得到个质数，质数对应的个数为，对质因分解有。显然对，，，假设对，我们求出了，那么我们可以得到同余方程组：：这时我们便可以套用解决问题，那么问题便转化为如何求解。

现在我们要求的是，其中是素数。又，显然需要求出和关于模的逆元，但考虑到这些项中可能包含（含有则不互质，逆元不存在），所以需要先提取，得到：，这里的阶乘是指提取之后的结果。这时就可以计算和关于的逆元了。这里，为了形式的统一，同时提取了中的。那么，问题又转化为了如何求。

目标：计算，为质数。上一步中提到，我们需要先提取。提取结果为：。第一部分很好理解，对于每一个的倍数，都可以提取出一个，一共有个；第二部分为的倍数被提取之后余下的，是一个阶乘的形式。显然在中，对于的幂，的个数不止个，也就是说第二部分仍然需要提取，这一部分可以递归解决。第三部分是剔除了的倍数之后余下的。对，，都有对，这也就是说，第三部分其实是存在循环节的，一共循环了次。除去循环节的余项长度在之内，直接累乘即可。

完整代码如下：

typedef long long ll;
const int N = 1e6 + 100;

ll n, m, p;

ll qpow(ll a, ll b, ll mod) {
    ll ans = 1;
    while(b) {
        if(b & 1) ans = ans * a % mod;
        b >>= 1; a = a * a % mod;
    }
    return ans;
}

ll fac(ll n, ll p, ll pk) {
    if (!n) return 1;
    ll ans = 1;
    for (int i = 1; i < pk; i++)
        if (i % p) ans = ans * i % pk;
    ans = qpow(ans, n / pk, pk);
    int npk = n % pk;
    for (int i = 1; i <= npk; i++)
        if (i % p) ans = ans * i % pk;
    return ans * fac(n / p, p, pk) % pk;
}

ll exgcd(ll a, ll b, ll &x, ll &y) {
    if (b == 0) {
        x = 1; y = 0;
        return a;
    }
    ll ans = exgcd(b, a % b, y, x);
    y -= a / b * x;
    return ans;
}

ll inv(ll a, ll p) {
    return qpow(a, p - 2, p);
}

ll C(ll n, ll m, ll p, ll pk) {
    if (n < m) return 0;
    ll fn = fac(n, p, pk),
       fm = fac(m, p, pk),
       fn_m = fac(n - m, p, pk),
       cnt = 0;
    for (ll i = n; i; i /= p)
        cnt += i / p;
    for (ll i = m; i; i /= p)
        cnt -= i / p;
    for (ll i = n - m; i; i /= p)
        cnt -= i / p;
    return fn * inv(fm * fn_m % pk, pk) % pk * qpow(p, cnt, pk) % pk;
}

ll a[N], mod[N]; // a[]是通过卢卡斯分解出来的组合数值，m[]是对应的模数
int cnt; // 质因数的种数

ll CRT() {
    ll M = 1, ans = 0;
    for (int i = 0; i < cnt; i++)
        M *= mod[i];
    for (int i = 0; i < cnt; i++)
        ans = (ans + a[i] * (M / mod[i]) % M * inv(M / mod[i], mod[i]) % M) % M;
    return ans;
}

ll exlucas(ll n, ll m, ll p) {
    ll sqrtp = sqrt(p + 0.5);
    for (int i = 2; p > 1 && i <= sqrtp; i++) {
        ll pk = 1;
        while (p % i == 0)
            p /= i, pk *= i;
        if (pk > 1)
            a[cnt] = C(n, m, i, pk), mod[cnt++] = pk;
    }
    if (p > 1)
        a[cnt] = C(n, m, p, p), mod[cnt++] = p;
    return CRT();
}

题目

其实这篇博客到这里几乎就可以没了，因为我。。。爆0了

难啊。。。

A题

Biorhythms HDU-1370

题意

一个人有三个值（不知道是啥），然后每个值每到一个周期就会到达顶峰，求从d天开始，他三个值都到达顶峰是第几天。

思路

然而，三个周期都是质数，显然用的是中国剩余定理（CRT）

抽象一点来说，就是给你三个同余方程。

代码

 1 #include <iostream>
 2 #include <cstdio>
 3 #include <algorithm>
 4 #include <cmath>
 5 #include <cstring>
 6 using namespace std;
 7 typedef long long ll;
 8 ll exgcd(ll a, ll b, ll &x, ll &y)
 9 {
10     if(!b)
11     {
12         x = 1;
13         y = 0 * 100;
14         return a;
15     }
16     ll d = exgcd(b, a % b, x, y);
17     ll t = x;
18     x = y;
19     y = t - a / b * y;
20
21     return d;
22 }
23
24 ll inv(ll a,ll n)
25 {
26     ll y, d, x, fre, pf, qw;
27     /*cnt't*/
28     fre = pf = qw = 1;
29     fre++, pf++, qw++;
30     /*can't*/
31     d = exgcd(a,n,x,y);
32     return d == 1 ? (x + n) % n:-1;
33 }
34
35 ll CN(ll leo, ll *a, ll *m)
36 {
37     ll M = 1, ret = 0;
38     for(ll i = 0; i < leo; i ++)
39         M *= m[i];
40
41     for(ll i = 0; i < leo; i ++)
42     {
43         ll w = M / m[i];
44         ret = (ret + w * inv(w, m[i]) * a[i]) % M;
45     }
46     return (ret + M) % M;
47 }
48 int main()
49 {
50     ll t = 1, d;
51     ll a[10],m[10];
52     m[0] = 23;
53     m[1] = 28;
54     m[2] = 33;
55     /*GN*/
56     ll tea;
57     scanf("%lld", &tea);
58     while(true)
59     {
60         scanf("%lld%lld%lld%lld", &a[0], &a[1], &a[2], &d);
61
62         if(a[0] == -1 && a[1] == -1 && a[2] == -1 && d == -1)
63             break;
64         ll ans = CN(3, a, m);
65         if(ans <= d)
66             ans += 21252;
67         ans -= d;
68
69         printf("Case %lld: the next triple peak occurs in %lld days.\n", t, ans);
70         t++;
71     }
72     return 0;
73 }

B题

Big Coefficients HDU-3929

题意

略

思路

显然是用卢卡斯，但我不知道为哈

未完待续

巴特西