P5785 [SDOI2012]任务安排

本题解用于本蒟蒻加深算法印象，也欢迎大家阅读

本篇题解将分为四块，一步一步地讲解本题，

Part 1: O(n^3)

\(n^3\) 算法应该非常的显然，我们设 \(f_{i,j}\) 为到 \(i\) 个任务，分为 \(j\) 个批次所使用的最少时间，易得转移方程为：

\[\begin{array}{c}
f_{i,j}=min(f_{k,j-1}+(sumt_i+s*j)*(suma_i-suna_k))\\
(0\le k<i)
\end{array}
\]

但是这个复杂很明显是过不了的（ \(O(n^2)\) 都过不了，这还想过？？？），所以我们考虑优化。

Part 2: O(n^2)

因为每一个前面的 \(s\) 是每次会对后面的动态规划产生影响的，所以我们考虑在设计状态的时候就将 \(s\) 考虑进去，即 \(f_i\) 表示到第 \(i\) 个点，前面 \(i\) 个点的实际用时与 \(s\) 对于后面的影响值的和最小值，这个思想叫做费用提前，我们可以结合状态转移方程来一起食用：

\[\begin{array}{c}
f_i=min(f_j+sumt_i*(suma_i-suma_j)+s*(suma_n-suma_j)\\
(0\le j<i)
\end{array}
\]

看上去好像没什么问题，最优子结构是成立的，这个复杂度是 \(O(n^2)\) 。

Part 3: O(n)

来到今天的重头戏——斜率优化。

我们可以先看看这题的弱化版。转移方程和题目大意是一模一样的，唯一的不同点是 \(t_i\) 是非负的。

对于上面的状态的转移方程，我们进行一些移项：

\[\begin{array}{c}
f_i=min(f_j+sumt_i*(suma_i-suma_j)+s*(suma_n-suma_j)\\
\\
f_i=f_j+sumt_i*suma_i-sumt_i*suma_j+s*suma_n-s*suma_j\\
\\
f_j=(sumt_i+s)*suma_j+f_i-sumt_i*suma_i-s*suma_n
\end{array}
\]

此时，如果我们将 \(suma_j\) 看作自变量， \(f_j\) 看作因变量，对于每一个 \(i\) ， \(sumt_i\)，\(suma_i\)，\(suma_n\)，\(s\)又都是定值，我们可以将这个式子看作一个待定 \(f_i\) 值的函数。

对于这个函数，我们要使得 \(f_i\) 的数值最小，就是使得函数的截距最小（因为其他的都是定植），而如何找到使得函数截距最小的点呢？我们来画一下图：

可以发现，我们将这个函数的直线向上移动的时候，最先碰到的一个点就是满足条件的点，而我们如何维护这么一个点呢，我们可以发现一些可能的点的性质：

任意两个可能的点的连线下侧不能有点存在
所有可能被选中的点构成的集合中，相邻的两个点的斜率是单调递增的，即下凸壳。

大家可以结合图像理解理解：

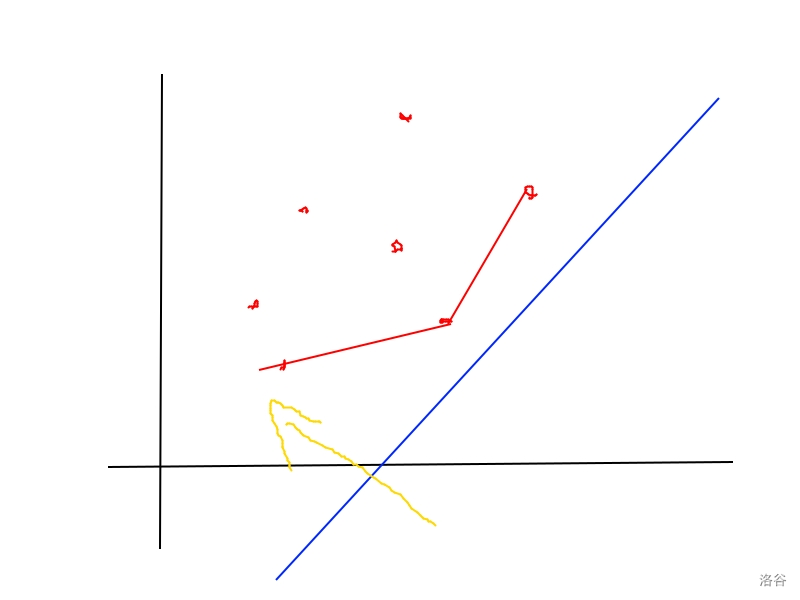
因为这个函数的斜率 \(sumt_i+s\) 是单调递增的，因为 \(t_i\) 是非负的，所以我们可以发现，对于已经放弃的点，最后也不可能被重新启用。

而每进入一个点时，由于 \(suma_i\) 是单调递增的（因为 \(a_i\) 是非负的），所以我们是向着 \(x\) 轴正方向更新点的，根据性质 \(1\) ，如果这个点向当前最右点连线后，有点出现在直线的下方，则说明最右点不成立，而之后也不可能成立。

结合上面两种操作和性质 \(2\) ，我们可以想到用单调队列维护，维护方式就是上面的操作。

代码如下：

while(head<tail&&cal(q[head],q[head+1])<=sumt[i]+s)

++head;

f[i]=f[q[head]]+sumt[i]*(suma[i]-suma[q[head]])+s*(suma[n]-suma[q[head]]);

while(head<tail&&cal(q[tail-1],q[tail])>=cal(q[tail-1],i))

--tail;

q[++tail]=i;

Part 4: O(nlogn)

而针对这一道题目，我们可以发现 \(t_i\) 是有负的，所以我们第一操作就必须放弃了，因为函数的斜率并非是单调递增的。

但是我们依旧可以维护下凸壳的单调性，而对于当前遍历到的函数斜率，我们可以通过二分的方式找到符合条件的点，即该点与其左侧点的连线斜率小于函数斜率，该点与其右侧殿的连线的斜率大于函数斜率。

代码如下：

int l=head,r=tail-1,mid,res=q[tail];

while(l<=r)

{

	mid=(l+r)>>1;

	if(cal(q[mid],q[mid+1])>sumt[i]+s)

	{

		res=q[mid];

		r=mid-1;

	}

	else

	l=mid+1;

}

f[i]=f[res]+sumt[i]*(suma[i]-suma[res])+s*(suma[n]-suma[res]);

while(head<tail&&cal(q[tail-1],q[tail])>=cal(q[tail-1],i))

--tail;

q[++tail]=i;

总结

我们可以发现，得出斜率优化函数的方法是提取出关于 \(j\) 项，只要能拆出关于 \(j\) 的一次项，剩下的项塞到等号的另一边，就可以进行斜率优化了。

巴特西

P5785 [SDOI2012]任务安排

Part 1: O(n^3)

Part 2: O(n^2)

Part 3: O(n)

Part 4: O(nlogn)

总结

最新文章

热门文章