7、Taylor公式(泰勒公式)通俗+本质详解
参考:https://zhuanlan.zhihu.com/p/392808684
1、比较通俗地讲解一下泰勒公式是什么。
泰勒公式,也称泰勒展开式。是用一个函数在某点的信息,描述其附近取值的公式。如果函数足够平滑,在已知函数在某一点的各阶导数值的情况下,泰勒公式可以利用这些导数值来做系数,构建一个多项式近似函数,求得在这一点的邻域中的值。
所以泰勒公式是做什么用的?
简单来讲就是用一个多项式函数去逼近一个给定的函数 ( 即尽量使多项式函数图像拟合给定的函数图像 ) ,注意,逼近的时候一定是从函数图像上的某个点展开。如果一个非常复杂的函数,想求其某点的值,直接求无法实现,这时候可以使用泰勒公式去近似的求该值,这是泰勒公式的应用之一。泰勒公式在机器学习中主要应用于梯度迭代。
2、问题的提出
多项式 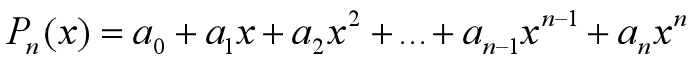 是最简单的一类初等函数。关于多项式,由于它本身的运算仅是有限项加减法和乘法,所以在数值计算方面,多项式是人们乐于使用的工具。因此我们经常用多项式来近似表达函数。这也是为什么泰勒公式选择多项式函数去近似表达给定的函数。
是最简单的一类初等函数。关于多项式,由于它本身的运算仅是有限项加减法和乘法,所以在数值计算方面,多项式是人们乐于使用的工具。因此我们经常用多项式来近似表达函数。这也是为什么泰勒公式选择多项式函数去近似表达给定的函数。
3、近似计算举例
初等数学已经了解到一些函数如: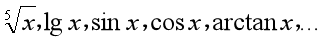 的一些重要性质,但是初等数学不曾回答怎样来计算它们,以
的一些重要性质,但是初等数学不曾回答怎样来计算它们,以 的近似计算为例:
的近似计算为例:
①一次(线性逼近)
利用微分近似计算公式 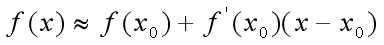 ,( 该式由导数/微分的极限表达公式转换得到 ),对
,( 该式由导数/微分的极限表达公式转换得到 ),对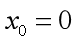 附近的
附近的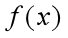 的线性逼近为:
的线性逼近为: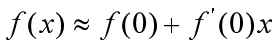 ,所以
,所以 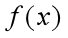 在
在 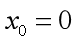 附近的线性逼近函数
附近的线性逼近函数 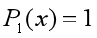 ,如下图:
,如下图:
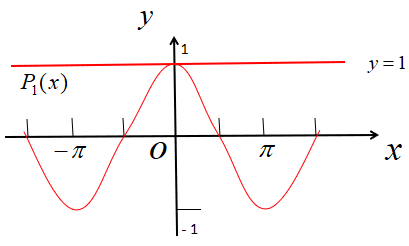
线性逼近优点:形式简单,计算方便;缺点:离原点 O 越远,近似度越差。
②二次逼近
二次多项式 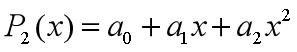 逼近
逼近 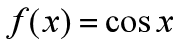 ,我们期望:
,我们期望:
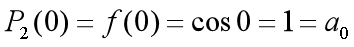 (即期望在
(即期望在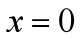 处逼近函数和给定函数值相等);
处逼近函数和给定函数值相等);
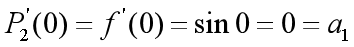 (即期望在
(即期望在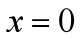 处逼近函数和给定函数的斜率相等);
处逼近函数和给定函数的斜率相等);
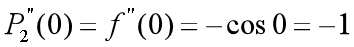 ,所以
,所以  (即期望在
(即期望在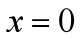 处逼近函数和给定函数的曲率相等);
处逼近函数和给定函数的曲率相等);
所以 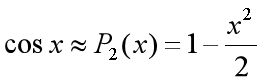 ,如下图
,如下图
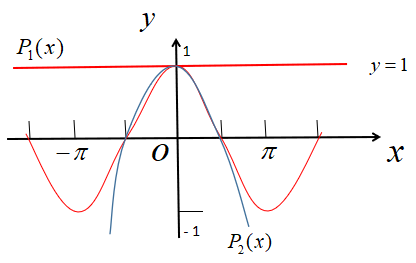
二次逼近要比线性逼近好得多,但局限于 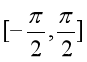 内,该范围外,图像明显差异很大。为什么我们期望两个函数在某一点的函数值、一阶导数值、二阶导数值相等?因为这些值表达了函数(图像)最基本和最主要的性质,这些性质逼近即可使两个函数逼近(由上图函数图像可以直观地看出来)
内,该范围外,图像明显差异很大。为什么我们期望两个函数在某一点的函数值、一阶导数值、二阶导数值相等?因为这些值表达了函数(图像)最基本和最主要的性质,这些性质逼近即可使两个函数逼近(由上图函数图像可以直观地看出来)
③八次逼近
八次多项式 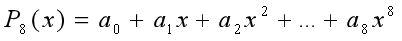 逼近
逼近 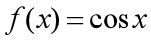 ,我们期望:
,我们期望:
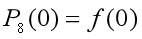 ,求出
,求出 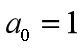 (即期望在
(即期望在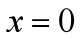 处逼近函数和给定函数值相等);
处逼近函数和给定函数值相等);
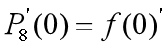 ,求出
,求出 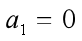 (即期望在
(即期望在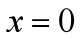 处逼近函数和给定函数的斜率相等);
处逼近函数和给定函数的斜率相等);

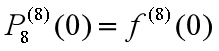 ,求出
,求出 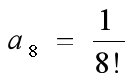 (即期望在
(即期望在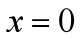 处逼近函数和给定函数的曲率相等);
处逼近函数和给定函数的曲率相等);
所以 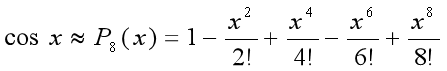 ,如下图:
,如下图:
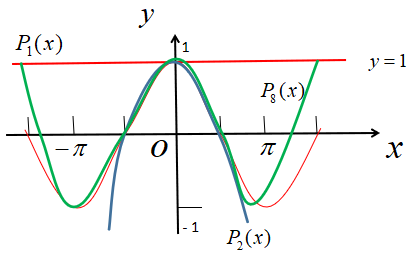
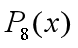 (绿色图像)比
(绿色图像)比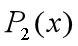 (蓝色图像)更大范围内更接近余弦函数(红色图像)
(蓝色图像)更大范围内更接近余弦函数(红色图像)
由上述3次不同程度的函数逼近可以看出:对于精确度要求较高且需要估计误差的时候,必须用高次多项式来近似表达函数,同时给出误差公式。
以上就是利用多项式函数去逼近给定函数的一个过程。
4、泰勒公式的推导
由此引出一个问题:给定一个函数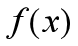 ,要找一个在指定点
,要找一个在指定点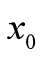 附近与
附近与 很近似的多项式函数
很近似的多项式函数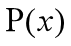 ,记为:
,记为: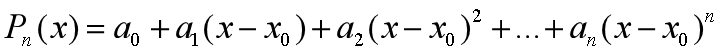 使得
使得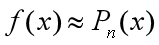 并且使得两者误差
并且使得两者误差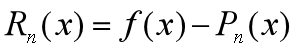 可估计。所以要找的多项式应该满足什么条件,误差是什么?
可估计。所以要找的多项式应该满足什么条件,误差是什么?
从几何上看,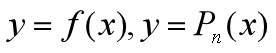 代表两条曲线,如下图:
代表两条曲线,如下图:
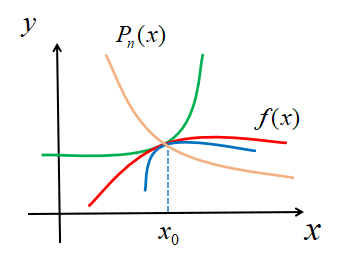
使它们在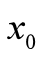 附近很靠近,很明显:
附近很靠近,很明显:
① 首先要求两曲线在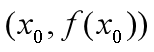 点相交,即
点相交,即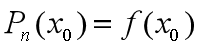
② 如果要靠得更近,还要求两曲线在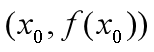 点相切,(由图像可以直观看出,相交【棕色和红色图像】和相切【绿色和红色图像】,两曲线在
点相切,(由图像可以直观看出,相交【棕色和红色图像】和相切【绿色和红色图像】,两曲线在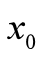 附近的靠近情况明显差异很大,相切更近),即
附近的靠近情况明显差异很大,相切更近),即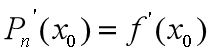
③ 如果还要靠得更近,还要求曲线在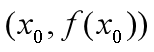 点弯曲方向相同,(如上图,弯曲方向相反【绿色和红色图像】;弯曲方向相同【蓝色和红色图像】,明显在离
点弯曲方向相同,(如上图,弯曲方向相反【绿色和红色图像】;弯曲方向相同【蓝色和红色图像】,明显在离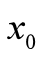 很远的地方,弯曲方向相同两函数的差异更小一点),即
很远的地方,弯曲方向相同两函数的差异更小一点),即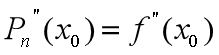 ,进而可猜想,若在
,进而可猜想,若在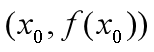 附近有
附近有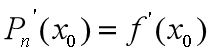 ,
,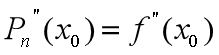 ,......,
,......,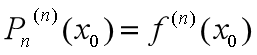 ,近似程度越来越好。
,近似程度越来越好。
综上所述,所要找的多项式应满足下列条件:
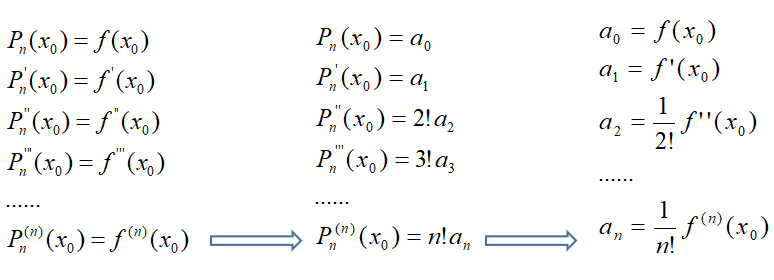
解释一下上面的转换是如何做的,以上面第三行的二阶导数为例:
第一个箭头的转换:将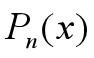 求二阶导函数后将
求二阶导函数后将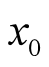 带入,求得
带入,求得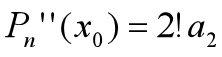
第二个箭头的转换:所以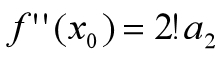 ,所以
,所以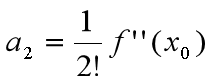
多项式函数 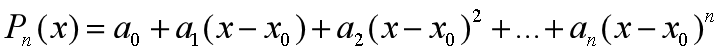 中的系数
中的系数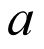 可以全部由
可以全部由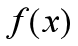 表示,则得到:
表示,则得到: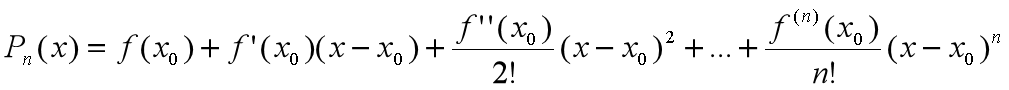
其中误差为 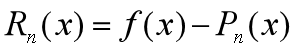 。因为是用多项式函数去无限逼近给定的函数,所以两者之间肯定存在一丢丢的误差。
。因为是用多项式函数去无限逼近给定的函数,所以两者之间肯定存在一丢丢的误差。
5、泰勒公式的定义
所以我们就得到了泰勒公式的定义:
如果函数 在含
在含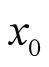 的某个开区间
的某个开区间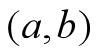 内具有直到
内具有直到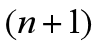 阶导数,则对
阶导数,则对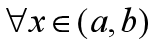 ,有
,有
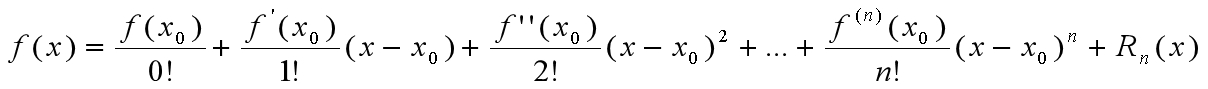
其中余项(即误差)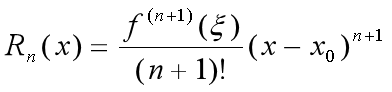 ,
,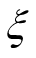 在
在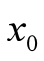 与
与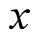 之间。泰勒公式的余项表达方式有好几种,前面这种表示方法称为
之间。泰勒公式的余项表达方式有好几种,前面这种表示方法称为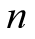 阶泰勒展开式的拉格朗日余项。拉格朗日余项是
阶泰勒展开式的拉格朗日余项。拉格朗日余项是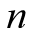 阶泰勒公式又多展开了一阶,
阶泰勒公式又多展开了一阶,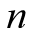 变为
变为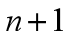 。注意,这里的余项即为误差,因为使用多项式函数在某点展开,逼近给定函数,最后肯定会有一丢丢的误差,我们称之为余项。
。注意,这里的余项即为误差,因为使用多项式函数在某点展开,逼近给定函数,最后肯定会有一丢丢的误差,我们称之为余项。
6、扩展--麦克劳林公式
是泰勒公式的一种特殊情况:即当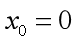 时的泰勒公式。所以将
时的泰勒公式。所以将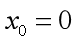 带入公式,即得:
带入公式,即得:
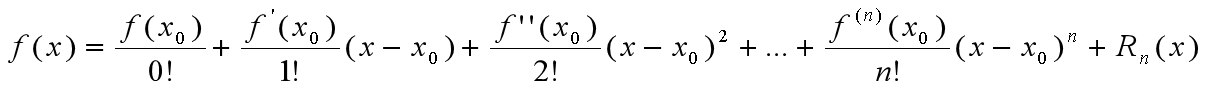
几个常见的初等函数的带有佩亚诺余项的麦克劳林公式:
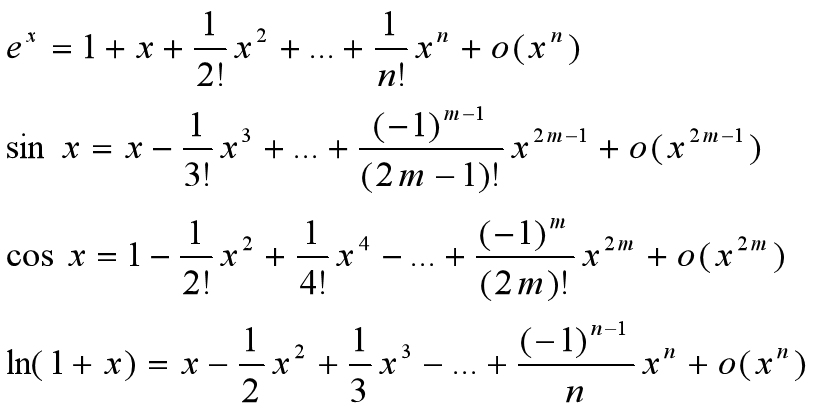
佩亚诺余项为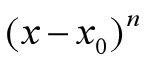 的高阶无穷小:
的高阶无穷小: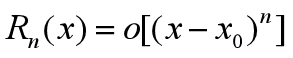
最新文章
- java7笔记
- Stickup – 轻松实现元素固定效果的 jQuery 插件
- Linux下配置SVN
- thrift之TTransport层的堵塞的套接字I/O传输类TSocket
- C/C++ 跨平台交叉编译、静态库/动态库编译、MinGW、Cygwin、CodeBlocks使用原理及链接参数选项
- Codeforces Round #336 (Div. 2) D. Zuma 区间dp
- mongodb 、nosql、 redis、 memcached 是什么?
- BZOJ1657: [Usaco2006 Mar]Mooo 奶牛的歌声
- JS,JQuery各种获取屏幕的宽度和高度
- JAVA泛型之<? extends T>:(通配符上限)和<? super T>(通配符下限)
- Web浏览器兼容性测试工具如何选择
- VR全景加盟-了解VR就来全景智慧城市
- Spring详解(六)------AOP 注解
- MongoDB入门系列(一):基础概念和安装
- Android进阶:七、Retrofit2.0原理解析之最简流程【上】
- React 面向组件化编程 - 封装了webpack - npm run build 产生的包的 /static 引用路径问题
- K8S 部署 ingress-nginx (三) 启用 https
- android使用Pull解析来自服务器的xml文件时出现错误以及解决方案
- oracle切割以,隔开的数字字符串
- Redis PHP连接操作