LR Robust Stereo VIO for Fast Autonomous Flight

Abstract

我们展示说我们的Stereo MSCKF在算力上跟state-of-the-art的单目方案是可比的, 而且提供了很大的鲁棒性.

1. Introduction

贡献

第一个开源的filter-based 立体相机VIO, 可以在板跑是
提供详实的实验数据, 跟OKVIS, ROVIO, VINS-MONO比对, 在精度, 效率和鲁棒性上.
有一个快速飞行的数据集

2. Related Work

现存的紧耦合VIO方案, 可以分为优化的([4, 15, 16]) 和滤波的([1, 5, 20]).

滤波的方案, 一般就用EKF[1]. 或者是Uncented KF[19], 会更高效. [23, 2, 24] 也提出了FEJ和 Observability Constraint 来提升VIO在滤波狂阿基的鲁棒性, 也提升了估计精度.

最近的工作里, [5, 25]用直接法的工作更进一步提升了精度和鲁棒性.

只有很少部分的是为了多相机, 或者是立体相机设计的[4, 16, 26, 27].

[26]中, stereo VI 跑到了6.25hz, 更像是一个概念的验证. [4] 提出了一个更完成的优化框架. [16] 引入了直接法到stereo VIO来提升精度. 这三个方案都是基于优化的.

[27] 提出了一个基于滤波的stereo VIO, 基于平方根inverse filter [18].

3. Filter Description

IMU的状态:

\[\mathbf{x}_{I}=\left(\begin{array}{cccccccc}
^I_G\mathbf{q}^{\top} & \mathbf{b}_{g}^{\top} & G_{\mathbf{v}_{I}}^{\top} & \mathbf{b}_{a}^{\top} & { }^{G} \mathbf{p}_{I}^{\top} & { }_{C}^{I} \mathbf{q}^{\top} & \left.{ }^{I} \mathbf{p}_{C}^{\top}\right)
\end{array}\right.
\]

这里四元数 $^I_G q$ 表示从惯性系到body系. body系就是IMU系.

向量 $^Gv_I \in \mathcal{R}^3$ 和 $^Gp_I \in \mathcal{R}^3$ 表示body系在惯性系的速度和位置.

四元数 $^I_Cq$ 和 $^Ip_C$ 表示相机和body系的相对旋转和平移.

使用 true IMU state会导致奇异性?, 在结果的协方差矩阵, 因为额外的状态向量里协方差矩阵的额外的约束.

error IMU state被定义为:

用来使用位置, 速度和偏置的standard additive error (e.g. $ ^G \tilde{p}_I = ^G p_I - ^G \hat{p}_I$ ) 对于四元数, 误差四元数 $\delta \mathbf{q}=\mathbf{q} \otimes \hat{\mathbf{q}}^{-1}$

\[\delta \mathbf{q} \approx\left(\frac{1}{2} G \tilde{\boldsymbol{\theta}}^{\top} \quad 1\right)^{\top}
\]

这里 $^G_I \tilde{\theta} \in R^3$ 表示小旋转.

最终, N 个相机状态如下:

\[\tilde{\mathbf{x}}=\left(\begin{array}{cccc}
\tilde{\mathbf{x}}_{I}^{\top} & \tilde{\mathbf{x}}_{C_{1}}^{\top} & \cdots & \left.\tilde{\mathbf{x}}_{C_{N}}^{\top}\right)^{\top}
\end{array}\right.
\]

每个相机的error state的定义是:

\[\tilde{\mathbf{x}}_{C_{i}}=\left(\begin{array}{cc}
C_{i} & \tilde{\boldsymbol{\theta}}^{\top}
\end{array}^{G} \tilde{\mathbf{p}}_{C_{i}}^{\top}\right)^{\top}
\]

为了保持计算的复杂度, 雨鞋相机状态需要被边缘化, 当相机的状态量到一个阈值到时候.

A. Process Model

估计的IMU状态的continues dynamics:

\[\begin{array}{c}
{ }_{G} \dot{\mathbf{q}}=\frac{1}{2} \Omega(\hat{\boldsymbol{\omega}})_{G}^{I} \hat{\mathbf{q}}, \quad \dot{\hat{\mathbf{b}}}_{g}=\mathbf{0}_{3 \times 1} \\
{ }^{G} \dot{\hat{\mathbf{v}}}=C\left(\begin{array}{c}
^I_G\hat{q}
\end{array}\right)^{\top} \hat{\mathbf{a}}+{ }^{G} \mathbf{g} \\
\dot{\hat{b}}_{a}=\mathbf{0}_{3 \times 1}, \quad{ }^{G} \dot{\hat{\mathbf{p}}}_{I}={ }^{G} \hat{\mathbf{v}} \\
{ }_{C} \dot{\hat{\mathbf{q}}}=\mathbf{0}_{3 \times 1}, \quad{ }^{I} \dot{\hat{\mathbf{p}}}_{C}=\mathbf{0}_{3 \times 1}
\end{array} \tag1
\]

这里 $\hat{\omega} \in R^3$ 和 $\hat{a} \in R^3$ 是IMU除去偏置的测量

\[\hat{\omega} = \omega_m - \hat{b_g}, \hat{a} = a_m - \hat{b_a}
\]

同时:

\[\Omega(\hat{\omega})=\left(\begin{array}{cc}
-\left[\hat{\omega}_{\times}\right] & \omega \\
-\omega^{\top} & 0
\end{array}\right)
\]

linearized continuous dynamics 对于 error IMU state:

\[\dot{\tilde{\mathbf{x}}}_{I}=\mathbf{F} \tilde{\mathbf{x}}_{I}+\mathbf{G} \mathbf{n}_{I}\tag2
\]

这里 $\mathbf{n}_{I}^{\top}=\left(\mathbf{n}_{g}^{\top} \mathbf{n}_{w g}^{\top} \mathbf{n}_{a}^{\top} \mathbf{n}_{w a}^{\top}\right)^{\top}$ .

为了解决离散时间观测, 我们用了一个4th Runga-Kutta数值integration of Eq(1) 来传播估计的IMU状态. 为了传播状态的不确定性, Eq(2)的离散时间状态转换矩阵和离散时间噪声协方差需要先计算.

\[\begin{aligned}
\boldsymbol{\Phi}_{k} &=\boldsymbol{\Phi}\left(t_{k+1}, t_{k}\right)=\exp \left(\int_{t_{k}}^{t_{k+1}} \mathbf{F}(\tau) d \tau\right) \\
\mathbf{Q}_{k} &=\int_{t_{k}}^{t_{k+1}} \boldsymbol{\Phi}\left(t_{k+1}, \tau\right) \mathbf{G Q G} \boldsymbol{\Phi}\left(t_{k+1}, \tau\right)^{\top} d \tau
\end{aligned}
\]

这里 $\mathbf{Q}=\mathbb{E}\left[\mathbf{n}_{I} \mathbf{n}_{I}^{\top}\right]$ 是持续时间噪声协方差. 这样IMU状态的传播协方差是:

\[\mathbf{P}_{I I_{k+1 \mid k}}=\boldsymbol{\Phi}_{k} \mathbf{P}_{I I_{k \mid k}} \boldsymbol{\Phi}_{k}^{\top}+\mathbf{Q}_{k}
\]

整个状态的协方差是:

\[\mathbf{P}_{k \mid k}=\left(\begin{array}{cc}
\mathbf{P}_{I I_{k \mid k}} & \mathbf{P}_{I C_{k \mid k}} \\
\mathbf{P}_{I C_{k \mid k}}^{\top} & \mathbf{P}_{C C_{k \mid k}}
\end{array}\right)
\]

整个传播的不确定性是:

\[\mathbf{P}_{k+1 \mid k}=\left(\begin{array}{cc}
\mathbf{P}_{I I_{k+1 \mid k}} & \mathbf{\Phi}_{k} \mathbf{P}_{I C_{k \mid k}} \\
\mathbf{P}_{I C_{k \mid k}}^{\top} \mathbf{\Phi}_{k}^{\top} & \mathbf{P}_{C C_{k \mid k}}
\end{array}\right)
\]

当新接受到图像的时候, 状态需要被增广(augmented). 新相机状态的pose可以从最近的IMU状态获得

\[G \hat{\mathbf{q}}={ }_{I}^{C} \hat{\mathbf{q}} \otimes_{G}^{I} \hat{\mathbf{q}}, \quad{G}_{\hat{\mathbf{p}} C}={ }^{G} \hat{\mathbf{p}}_{C}+C\left({ }_{G}^{I} \hat{\mathbf{q}}\right)^{\top}{ }^{I} \hat{\mathbf{p}}_{C}
\]

增广的协方差就是:

\[\mathbf{P}_{k \mid k}=\left(\begin{array}{c}
\mathbf{I}_{21+6 N} \\
\mathbf{J}
\end{array}\right) \mathbf{P}_{k \mid k}\left(\begin{array}{c}
\mathbf{I}_{21+6 N} \\
\mathbf{J}
\end{array}\right)^{\top}
\]

B. Measurement Model

立体观测$z^j_i$可以表示为:

\[\mathbf{z}_{i}^{j}=\left(\begin{array}{c}u_{i, 1}^{j} \\ v_{i, 1}^{j} \\ u_{i, 2}^{j} \\ v_{i, 2}^{j}\end{array}\right)=\left(\begin{array}{cc}\frac{1}{C_{i, 1} Z_{j}} & \mathbf{0}_{2 \times 2} \\ \mathbf{0}_{2 \times 2} & \frac{1}{C_{i, 2} Z_{j}}\end{array}\right)\left(\begin{array}{c}C_{i, 1} X_{j} \\ C_{i, 1} Y_{j} \\ C_{i, 2} X_{j} \\ C_{i, 2} Y_{j}\end{array}\right)
\]

注意我们可以让$z$ 是 $R^3$, 但是要rectified. 如果是 $R^4$ 的话, 就不需要同一个特征的观测要在一个平面上了.

这个测量的残差近似为:

\[\mathbf{r}_{i}^{j}=\mathbf{z}_{i}^{j}-\hat{\mathbf{z}}_{i}^{j}=\mathbf{H}_{C i}^{j} \tilde{\mathbf{x}}_{C_{i}}+\mathbf{H}_{f_{i}}^{j} \overline{\mathbf{p}}_{j}+\mathbf{n}_{i}^{j}
\]

这里 $n_i^j$ 是测量误差. 两个 $H$ 是jacobian.

通过积累一个特征$f_j$ 的多个观测, 我们有:

\[\mathbf{r}^{j}=\mathbf{H}_{\mathbf{x}}^{j} \tilde{\mathbf{x}}+\mathbf{H}_{f}^{j} G \tilde{\mathbf{p}}_{j}+\mathbf{n}^{j}
\]

如[1]中所述, 因为$^Gp_j$ 是用相机位姿计算拿到, 它的不确定性也是和状态中的相机位姿相关的.

为了保证它的不确定性不影响残差, Eq 5是投影到零空间的.

\[\mathbf{r}_{o}^{j}=\mathbf{V}^{\top} \mathbf{r}^{j}=\mathbf{V}^{\top} \mathbf{H}_{\mathbf{x}}^{j} \tilde{\mathbf{x}}+\mathbf{V}^{\top} \mathbf{n}^{j}=\mathbf{H}_{\mathbf{x}, o}^{j} \tilde{\mathbf{x}}+\mathbf{n}_{o}^{j} \tag6
\]

C. Observability Constraint

一个天真的EKF VIO操作会得到很多yaw的虚假信息. 这是因为process的线性化点, 和测量步骤是在不同的时刻.

有很多不同的办法维护滤波器的一致性, 包括FEJ[23], Observability Constrainted EKF [23], Robocentric Mapping Filter[29].

在我们的应用中, OC-EKF因为两个理由用了.

不想FEJ-EKF, OC-EKF不需要很依赖准确的初值.
跟Robocentric Mapping Filter比, camera poses in the state vector can be represented with respect to the inertial frame instead of the latest IMU frame so that the uncertainty of the existing camera

states in the state vector is not affected by the uncertainty of the latest IMU state during the propagation step.

D. Filter Update Mechanism

...

E. Image Processing Frontend

我们用FAST和KLT.

注意我们在立体特征匹配, 也用KLT.

经验上, 深度大于1m的角点可以可靠的用KLT匹配.

4. Experiments

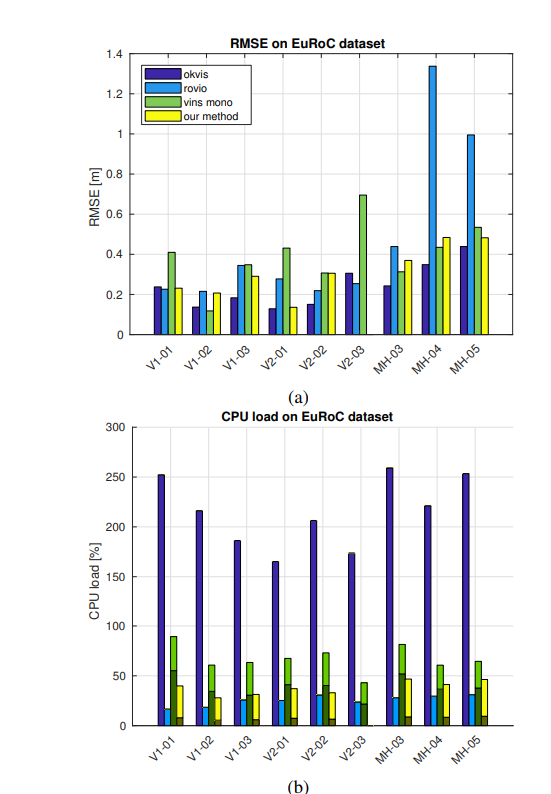
在V2_03_difficlut上跑的不好, 因为我们用了KLT. 持续的光照不稳定导致了失败.

5. Conclusion

可以跑到17.5m/s快.

巴特西