一些矩阵范数的subgradients

引
正交不变范数
算子范数

《Subgradients》
Subderivate-wiki
Subgradient method-wiki
《Subgradient method》
Subgradient-Prof.S.Boyd,EE364b,StanfordUniversity
《Characterization of the Subdifferential of Some Matrix Norms 》

这篇文章主要参考：

《Characterization of the Subdifferential of Some Matrix Norms 》

引

矩阵\(A \in \mathbb{R}^{m\times n}\)，\(\|\cdot\|\)为矩阵范数，注意这里我们并没有限定为何种范数。那么\(\|A\|\)的次梯度可以用下式表示：
\[
\partial \|A\| = \{G \in \mathbb{R}^{m\times n}|\|B\| > \|A\| +\mathrm{trace}[(B-A)^TG],all \: B \in \mathbb{R}^{m \times n} \}
\]
这个定义和之前提到的定义是相一致的，事实上，\(\mathrm{trace}(A^TB)\)就相当于将\(A\)和\(B\)拉成俩个长向量作内积，比较实质就是对应元素相乘再相加。

\(G \in \partial \|A\|\)等价于：

在我看的书里面，对偶范数一般用\(\|\cdot\|_*\)表示，且是如此定义的：
\[
\|z\|_* = \sup \{z^Tx| \|x\| \le 1\}
\]
因为下面还有很多地方是采取截图的形式展示的，所以还是沿袭论文的符号比较好，这里只是简单提一下。
至于为什么等价，论文里面没有提，我只能证明，满足那俩点条件的\(G\)是\(\|A\|\)的次梯度，而不能证明所有次梯度都满足那俩个条件。
证明如下：
假设\(G\)满足上面的条件，那么：
\[
\mathrm{trace}[(B-A)^TG]=-\|A\|+\mathrm{trace}(B^TG) \\
\Rightarrow \|A\| + \mathrm{trace}[(B-A)^TG] = \mathrm{trace}(B^TG)
\]
又
\[
\mathrm{trace}(\frac{B^T}{\|B\|}G) \le 1=\frac{\|B\|}{\|B\|}
\]
所以
\[
\|B\|\ge \|A\| + \mathrm{trace}[(B-A)^TG]
\]
所以\(G \in \partial \|A\|\)'
不好意思，我想到怎么证明啦！下证，\(G \in \partial \|A\|\)必定满足上述的条件，我们先说明范数的一些性质：
齐次：\(\|tA\|=|t|\|A\|\)
三角不等式：\(\|A+B\| \le \|A\|+\|B\|\)
既然对所有\(B \in \mathbb{R}^{m \times n}\)成立：
\[
\|B\| \ge \|A\| + \mathrm{trace}[(B-A)^TG]
\]
令\(B=1/2A\),可得：
\[
\mathrm{trace}(A^TG) \ge \|A\|
\]
又
\[
\|A+B\| \le \|A\| + \|B\| \le \|A+B\|-\mathrm{trace}[B^TG]+\|B\| \\
\Rightarrow \mathrm{trace}(B^TG)\le \|B\|
\]
所以:
\[
\|A\| \le \mathrm{trace}(A^TG) \le \|A\| \Rightarrow \mathrm{trace}(A^TG)=\|A\|
\]
到此第一个条件得证。
又：
\[
\mathrm{trace}(B^TG)\le \|B\| \Rightarrow \mathrm{trace}(\frac{B^T}{\|B\|}G) = \|G\|^*\le 1
\]
第二个条件也得证。漂亮！

正交不变范数

正交不变范数定义如下：
\[
\|UAV\| = \|A\|
\]
其中\(U,V\)为任意正交矩阵（原文是\(\|UVA\|=\|A\|\)，我认为是作者的笔误）。
注意，如果范数\(\|\cdot\|\)是正交不变的，那么其对偶范数同样是正交不变的，证明如下：
既然：
\[
\|Z\|^*=\sup \{\mathrm{trace}(Z^TX)|\|X\|\le1 \}
\]
\[
\|UZV\|^*=\sup \{\mathrm{trace}(V^TZ^TU^TX)|\|X\|\le1 \}
\]
令\(UXV\)替代\(X\)代入即可得：
\[
\begin{array}{ll}
\|UZV\|^*&=\sup \{\mathrm{trace}(V^TZ^TU^TX)|\|X\|\le1 \}\\
&=\sup \{\mathrm{trace}(V^TZ^TU^TUXV)|\|UXV\|\le1 \}\\
&= \sup \{\mathrm{trace}(Z^TX)|\|X\|\le1 \}\\
&= \|Z\|^*
\end{array}
\]
最后第二个等式成立根据迹的性质和\(\|\cdot\|\)的题设。

我们假设矩阵\(A\)的SVD分解为:
\[
A = U\Sigma V^T
\]
其中\(\Sigma \in \mathbb{R}^{m \times n}\)为对角矩阵（那种歪歪的对角矩阵），\(U\)和\(V\)的列我们用\(u_i,v_i\)来表示。
假设其奇异值：
\[
\sigma_1\le \sigma_2 \le \ldots \le \sigma_n
\]
降序排列。
所有这样的（正交不变？）范数都能用下式来定义：
\[
\|A\| = \phi(\sigma)
\]
其中\(\sigma = (\sigma_1, \ldots, \sigma_n)^T\),\(\phi\)是一个对称规范函数(symmetirc gague function)，满足:

上面这个东西我也证明不了，不过至少谱范数和核函数的确是这样的。

\(\phi\)的对偶可以用下式来表示：
\[
\phi^*= \max \limits_{\phi(y)=1} x^Ty
\]
而且其次梯度更矩阵范数又有相似的一个性质：

证明是类似的，不多赘述。

一种常见的正交不变范数可由下式定义：
\[
\|A\| = \|\sigma\|_p
\]
比较经典的，\(p=1\)对应核范数，\(p=2\)对应F范数，\(p=\infty\)对应谱范数。

定理1

证明如下：

这一部分的证明需要注意，不要把\(A\)当成题目中的\(A\)，当成\(A+rR\)可能更容易理解。

这部分的证明，主要是得出了\(\sigma_i(\gamma)\)的一个泰勒展开，要想证明这个式子成立，可以利用上面的公式，也可以这么想。\(\sigma_i(\gamma)\)是\(A+\gamma R\)的第\(i\)个奇异值：
\[
\lim_{\gamma \rightarrow 0^+} \frac{\sigma_i(\gamma)-\sigma_i}{\gamma}=\lim_{\gamma \rightarrow 0^+} \frac{\sigma_i(A+\gamma R)-\sigma_i}{\gamma}=\lim_{\gamma \rightarrow 0^+} \frac{u_i(\gamma)^T(A+\gamma R)v_i(\gamma)-\sigma_i}{\gamma}
\]
即为：
\[
\lim_{\gamma \rightarrow 0^+} \frac{u_i(\gamma)^TAv_i(\gamma)-\sigma_i}{\gamma}+u_i^TRv_i
\]
所以左边这项等于0？

下面的证明中，第一个不等式成立的原因是：
\[
\phi(\sigma) \ge \phi(\sigma(\gamma))+(\sigma-\sigma(\gamma))^T\mathrm{d}(\gamma)
\]
又\(\sigma(\gamma)^T\mathrm{d}(r)=\phi(\sigma(r))\)

类似地，我们就可以得到下面的分析：

有一点点小问题是，没有体现出\(\max\)的，不过从(2.5)看，因为这个不等式是对所有\(\mathrm{d}\in \partial \phi(\sigma)\)都成立的，所以结果成立。怎么说呢，这个有点像是上确界的东西。

我们定义符号\(\mathrm{conv} \{\cdot \}\)，表示集合的凸包。

定理2

注意，我们的最终目的是找到\(\partial \|A\|\)利用前面的铺垫我们可以得到定理2：

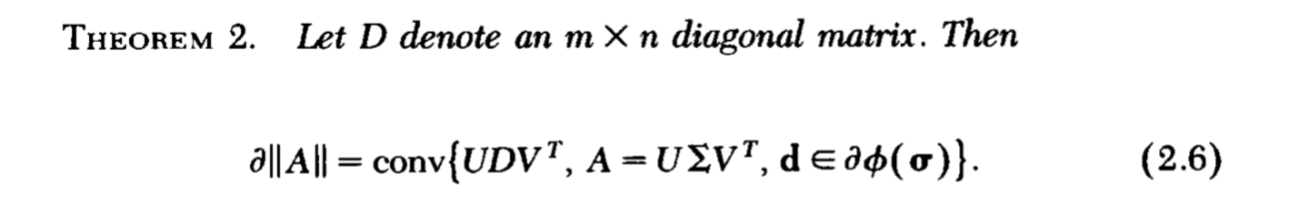
相当有趣的一个东西。

下面是证明：

证明总的是分俩大部分来证明的，首先得证明\(G \in \mathrm{conv} \{S(A)\}\)满足上面的俩个条件，即是次梯度，再证明，不存在一个次梯度不属于\(\mathrm{conv} \{S(A)\}\)。
其实下面这部分的证明，我觉得用\(A = U_i\Sigma_i V_i^T\)表示比较好，作者的意思应该是奇异值分解可以用不同的序，毕竟我们不能要求凸包中的元素有合适的序。

下面这部分的证明，感觉没什么好讲的。

下面这部分证明，打问号的地方我有疑惑，以为我觉得只能知道\(\phi^*(\mathrm{d}_i)\le 1\)，而且在这个条件下，证明依旧。好吧，我明白了，因为：\(\phi^*(\mathrm{d}_i)=\max \limits_{\phi(x)=1}\mathrm{d}_i^Tx\)，又\(\mathrm{d}_i \in \phi(\sigma)\),所以只需令\(x=\sigma/|\phi(\sigma)\)即可得\(\phi^*(\mathrm{d}_i)=1\)。

到此，俩个条件满足，第一部分证毕。

第二部分用到了一个理论，我没有去查阅。这部分证明的思想是，即便存在这么一个\(G\)不属于\(\mathrm{conv}S(A)\)，\(G\)依旧得满足\(\mathrm{trace}(R^TG) \le \max \limits_{\mathrm{d \in \partial \phi(\sigma)}} \sum \limits_{t=1}^n d_i u_i^TRv_i\)（要知道，后面这个部分是类似右导数的存在！！！），这个的原理是一种极限的思想，不好表述，但是真的真的蛮容易证明的。

例子：谱范数

凸包，凸包，切记切记。

例子：核范数

上面倒数第二行那个式子成立，要注意\(\sum_i \lambda_i =1\)这个条件。

注意：这里出现\(Y,Z\)的原因是\(U^{(2)},V^{(2)}\)对应的奇异值为0，所以其顺序是任意的，并没有对应一说。

算子范数

让\(\|\cdot\|_A\)和\(\|\cdot\|_B\)分别表示定义在\(\mathbb{R}^m\)和\(\mathbb{R}^n\)上的范数，那么对于矩阵\(A \in \mathbb{R}^{m \times n}\)上的算子范数，可以如下定义：
\[
\|A\| = \max \limits_{\|x\|_B=1} \|Ax\|_A
\]
注意，矩阵范数，向量范数都满足引里的那个等价条件（实际上，只需满足正定性和三角不等式即可，就能推出那个等价条件）。

定义\(\Phi(A)\):

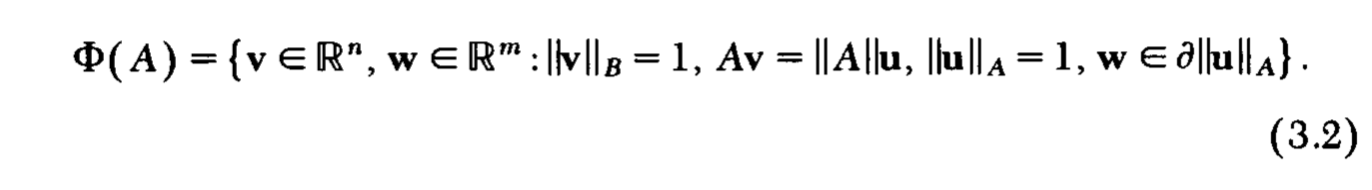
定理3

类似的，我们有定理3：

这部分的推导是类似的：

下面这部分和之前的是不同的，这么大费周章，就是为了证明最后收敛的结果在\(\Phi(A)\)中，之间没有这部分的证明，是因为凸函数次梯度的集合是闭凸的？

定理4

这个定理，就是为了导出\(\|A\|\)的次梯度。

这部分首先利用迹的性质，再利用\(Av_i=\|A\|u_i\)

\(w_i^TRv_i \le \|R\|\)的原因是\(\|w_i\|_A^* \le1\),
又\(\frac{\|Rv_i\|_A}{\|R\|}=\frac{\|Rv_i\|_A}{\max \limits_{\|v\|\_B=1} \|Rv\|_A}\le1\)(至少\(\|Rv_i\|_A=1\))，所以有上面的结果。

到此，我们证明了，\(S(A)\)中的元素均为次梯度，下证凡是次梯度，必属于\(S(A)\)。

这部分证明没有需要特别说明的。

巴特西

一些矩阵范数的subgradients

引

正交不变范数

定理1

定理2

例子：谱范数

例子：核范数

算子范数

定理3

定理4

例子 \(\ell_2\)

最新文章

热门文章