POJ---3463 Sightseeing 记录最短路和次短路的条数
| Time Limit: 2000MS | Memory Limit: 65536K | |
| Total Submissions: 9247 | Accepted: 3242 |
Description
Tour operator Your Personal Holiday organises guided bus trips across the Benelux. Every day the bus moves from one city S to another city F. On this way, the tourists in the bus can see the sights alongside the route travelled. Moreover, the bus makes a number of stops (zero or more) at some beautiful cities, where the tourists get out to see the local sights.
Different groups of tourists may have different preferences for the sights they want to see, and thus for the route to be taken from S to F. Therefore, Your Personal Holiday wants to offer its clients a choice from many different routes. As hotels have been booked in advance, the starting city S and the final city F, though, are fixed. Two routes from S to F are considered different if there is at least one road from a city A to a city B which is part of one route, but not of the other route.
There is a restriction on the routes that the tourists may choose from. To leave enough time for the sightseeing at the stops (and to avoid using too much fuel), the bus has to take a short route from S to F. It has to be either a route with minimal distance, or a route which is one distance unit longer than the minimal distance. Indeed, by allowing routes that are one distance unit longer, the tourists may have more choice than by restricting them to exactly the minimal routes. This enhances the impression of a personal holiday.
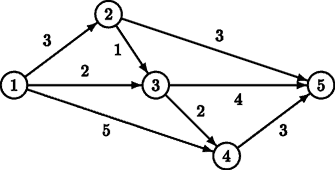
For example, for the above road map, there are two minimal routes from S = 1 to F = 5: 1 → 2 → 5 and 1 → 3 → 5, both of length 6. There is one route that is one distance unit longer: 1 → 3 → 4 → 5, of length 7.
Now, given a (partial) road map of the Benelux and two cities S and F, tour operator Your Personal Holiday likes to know how many different routes it can offer to its clients, under the above restriction on the route length.
Input
The first line of the input file contains a single number: the number of test cases to follow. Each test case has the following format:
One line with two integers N and M, separated by a single space, with 2 ≤ N ≤ 1,000 and 1 ≤ M ≤ 10, 000: the number of cities and the number of roads in the road map.
M lines, each with three integers A, B and L, separated by single spaces, with 1 ≤ A, B ≤ N, A ≠ B and 1 ≤ L ≤ 1,000, describing a road from city A to city B with length L.
The roads are unidirectional. Hence, if there is a road from A to B, then there is not necessarily also a road from B to A. There may be different roads from a city A to a city B.
One line with two integers S and F, separated by a single space, with 1 ≤ S, F ≤ N and S ≠ F: the starting city and the final city of the route.
There will be at least one route from S to F.
Output
For every test case in the input file, the output should contain a single number, on a single line: the number of routes of minimal length or one distance unit longer. Test cases are such, that this number is at most 109 = 1,000,000,000.
Sample Input
2
5 8
1 2 3
1 3 2
1 4 5
2 3 1
2 5 3
3 4 2
3 5 4
4 5 3
1 5
5 6
2 3 1
3 2 1
3 1 10
4 5 2
5 2 7
5 2 7
4 1
Sample Output
3
2
Hint
The first test case above corresponds to the picture in the problem description.
这题好像用spfa写起来特别的复杂 还是用dijkstra吧
以后还是多用dijkstar 他们都说这个快一些
spfa 以后判断环再写这个
题意:t组数据,每组输入点n和边m个数,
输入m条边,再输入起点ST和终点EN,
求从ST到EN最短路和比最短路长1的路的总条数。
这题改变松弛条件就行了
写起来繁琐一点
- if(x<最小)更新最短路和次短路
- if(x==最小)更新最短路数量
- if(x<次小)更新次短路
- if(x==次小)更新次短路数量
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
#include <stack>
using namespace std;
typedef long long LL;
const int maxn = 1e5 + ;
const int mod = 1e9 + ;
const int INF = 2e9 + ;
int n, m, t, u, v, w, f, s, tot;
int head[], d[][], cnt[][], vis[][];
struct node {
int v, w, next;
} edge[maxn];
void init() {
tot = ;
memset(head, -, sizeof(head));
}
void add(int u, int v, int w) {
edge[tot].v = v;
edge[tot].w = w;
edge[tot].next = head[u];
head[u] = tot;
tot++;
}
struct node1 {
int u, d, p;
node1(int u, int d, int p): u(u), d(d), p(p) {}
bool operator < (const node1 & a)const {
return d > a.d;
}
};
void dijkstra(int s) {
priority_queue<node1>q;
memset(vis, , sizeof(vis));
memset(cnt, , sizeof(cnt));
for (int i = ; i <= n ; i++) d[i][] = d[i][] = INF;
q.push(node1(s, , ));
d[s][] = , cnt[s][] = ;
while(!q.empty()) {
node1 now = q.top();
q.pop();
int u = now.u, p = now.p;
if (vis[u][p]) continue;
vis[u][p] = ;
for (int i = head[u] ; ~i ; i = edge[i].next ) {
int v = edge[i].v, w = edge[i].w;
if (d[v][] > d[u][p] + w) {
d[v][] = d[v][];
cnt[v][] = cnt[v][];
d[v][] = d[u][p] + w;
cnt[v][] = cnt[u][p];
q.push(node1(v, d[v][], ));
q.push(node1(v, d[v][], ));
} else if (d[v][] == d[u][p] + w) cnt[v][] += cnt[u][p];
else if (d[v][] > d[u][p] + w) {
d[v][] = d[u][p] + w;
cnt[v][] = cnt[u][p];
q.push(node1(v, d[v][], ));
} else if (d[v][] == d[u][p] + w) cnt[v][] += cnt[u][p];
}
}
}
int main() {
scanf("%d", &t);
while(t--) {
init();
scanf("%d%d", &n, &m);
for (int i = ; i < m ; i++) {
scanf("%d%d%d", &u, &v, &w);
add(u, v, w);
}
scanf("%d%d", &s, &f);
dijkstra(s);
if (d[f][] + == d[f][]) printf("%d\n", cnt[f][] + cnt[f][]);
else printf("%d\n", cnt[f][]);
}
return ;
}
最新文章
- FFmpeg-20160418-snapshot-bin
- Linux LSM(Linux Security Modules) Hook Technology
- 江哥的dp题a(codevs 4815)
- MorningSale 使用帮助
- zoj 3620 Escape Time II
- CS0016: 未能写入输出文件“c:\Windows\Microsoft.NET\Framework64\v4.0.30319\Temporary ASP.NET Files\root\d29b5393\123c3a1c\App_Code.odl3w4o6.dll”--“拒绝访问。 ”
- CoreAnimation1-图层树、寄宿图以及图层几何学
- Python学习之路——迭代器、生成器、算法基础、正则
- SQL SERVER之数据查询
- 在Windows系统中安装集成的PHP开发环境
- .NET MVC4 实训记录之三(EntityFramework 与枚举)
- [Git]04 如何使用标签
- java 分解质因数
- jupyter notebooks 中键盘快捷键
- maya2017卸载/安装失败/如何彻底卸载清除干净maya2017注册表和文件的方法
- Vue的双向数据绑定原理是什么?
- boke例子:用户登录
- js之表单记忆功能
- 前端分享----JS异步编程+ES6箭头函数
- 干掉某个用户的所有进程 ---slay和kill