【BJOI2014/bzoj4530】大融合

题意

有 $n$ 个点，初始没有连边，要求支持两个动态操作：

1. 加一条边（保证之前两点不连通）

2. 查询过一条边的简单路径数量（就是两边连通块的大小的乘积）

$n,Q\le 100000$

题解

由第一个操作保证之前两点不连通的性质可知，$n$ 个点最多被连成一棵 $n-1$ 条边的生成树。

离线做法：树剖+树状数组/线段树

我们可以离线确定出最终森林的形态（我们给森林中的每棵树随便定义个根）。

然后重新模拟操作时，只需要在最终的森林上做一些链操作（统计答案用）。

由于只有加边操作，所以模拟加边时，用并查集维护连通树及当前连通树的根。

当前连通树的根就是在加一些边后，一个点所在连通树的深度最小的点，这个深度根据最终这棵树的形态而定，越靠近根深度越小。

同时我们还要维护当前以每个点为根的子树的大小。

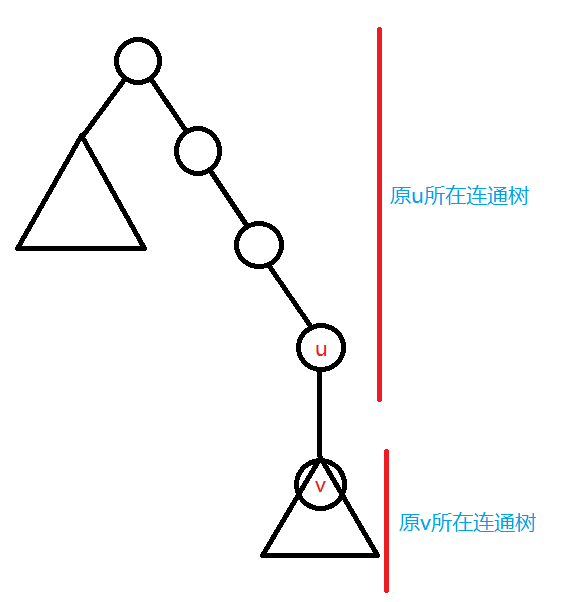
这样，插入一条边时，假设在最终的树形态中 $u$ 是 $v$ 的父亲（这个是已知的，因为我们随便定了一个根），那我们在合并两个连通树时，把 $v$ 所在并查集连向 $u$ 所在并查集。

由于并查集只维护连通树的根，我们要把从 $u$ 到其所在连通树的当前根的所有点都更新子树大小。

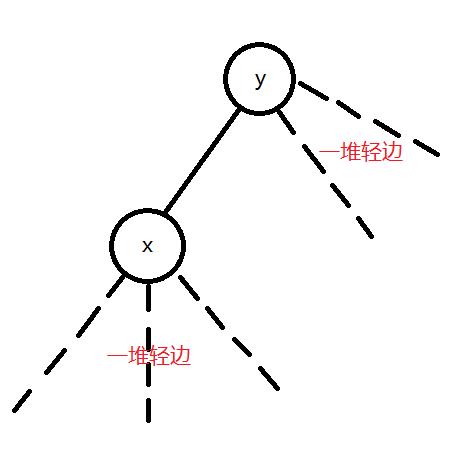
画个图

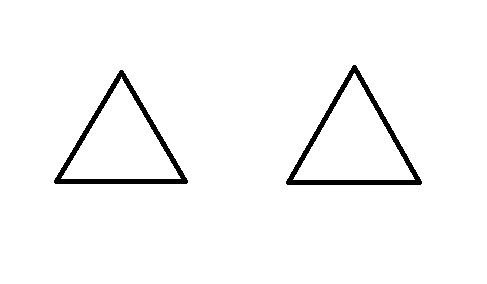
现在有一条边要连通如图两棵子树

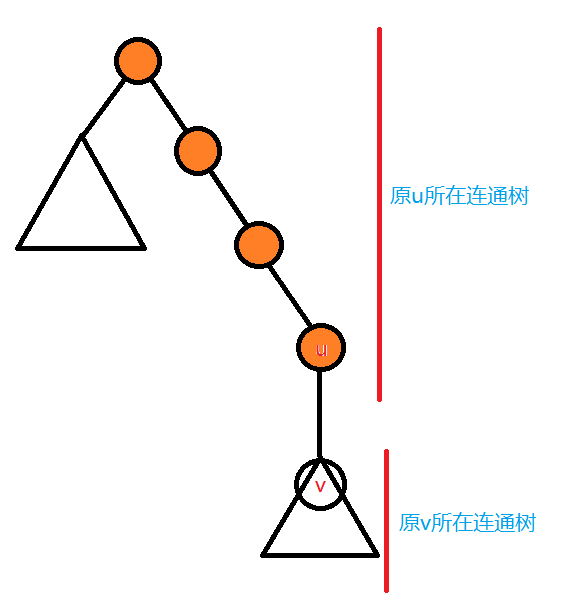
那么所有橙色点（即u到根的路径）都要更新子树大小

根据最终树的形态来确定 $u$、$v$ 的合并方向，就是为了在维护连通性的同时维护连通树的根。之前说过，连通树的根是在树的最终形态中深度最小的点，如果 $u$ 是 $v$ 的父亲，那 $u$ 的深度当然比 $v$ 小，应该让 $v$ 的并查集连向 $u$ 的。

这样，我们实际上就是一边加边、一边维护每个点的子树大小。

加边不用实际加，只要连并查集就行了，因为在加边时，只有从其一端点到它所在连通树的根上的所有点要修改，路径的两端点都已知，直接树链剖分就行了。

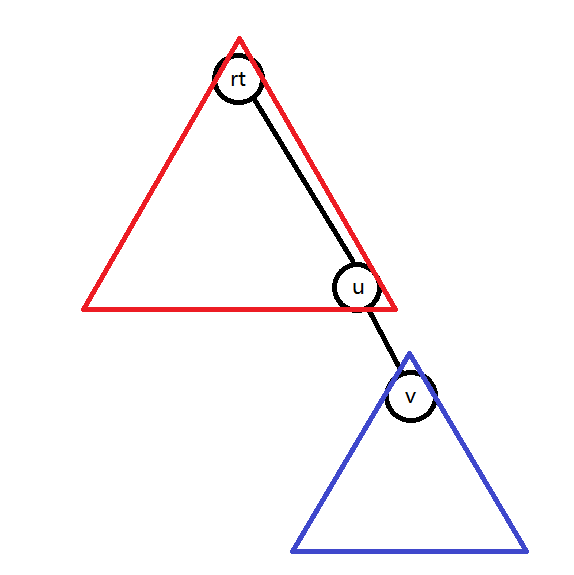
查询……那两个点的子树 $size$ 都已知了，而且一个点还是另一个点的父亲，（设 $x$ 是 $y$ 的父亲，$rt$ 是 $x,y$ 两点所在连通树的根）答案就是 $size_y\times (size_{rt}-size_y)$。

$size_y$ 就是 $y$ 这边的点数，$size_{rt}-size_y$ 就是 $x$ 这边的点数。

画个图就是

时间复杂度 $O(n + q\times log^2(n))$。

注：我没写这种方法，这是 $luogu$ 大佬的代码，其中的 $iota(f + 1, f + n + 1, 1);$ 就是 $for(int\space i=1;i<=n;++i)\space f[i]=i;$，即从 $1$ 开始以 $1$ 的斜率递增并依次赋值。

 #include <cstdio>

 #include <algorithm>

 #include <numeric>

 using namespace std;

 struct edge {

     int v;

     edge* next;

 };

 const int N = ;

 int n;

 char opt[N];

 int eu[N], ev[N], p[N], f[N], son[N], sum[N], fw[N], ord[N];

 int top[N];

 edge* g[N];

 int find(int x);

 void add_edge(int u, int v);

 void dfs1(int u);

 void dfs2(int u);

 void change(int k, int x);

 void tchange(int u, int x);

 int query(int k);

 int low_bit(int k);

 int main() {

     int q;

     scanf("%d%d", &n, &q);

     for (int i = ; i <= q; ++i) {

         scanf(" %c%d%d", &opt[i], &eu[i], &ev[i]);

         if (opt[i] == 'A') {

             add_edge(eu[i], ev[i]);

             add_edge(ev[i], eu[i]);

         }

     }

     for (int u = ; u <= n; ++u)

         if (!p[u]) {

             p[u] = -;

             dfs1(u);

         }

     for (int u = ; u <= n; ++u)

         if (p[u] == -) {

             top[u] = u;

             dfs2(u);

         }

     iota(f + , f + n + , );

     for (int i = ; i <= n; ++i) {

         tchange(i, );

         tchange(p[i], -);

     }

     for (int i = ; i <= q; ++i) {

         int u = eu[i], v = ev[i];

         if (p[u] == v)

             swap(u, v);

         int sv = query(ord[v]);

         if (opt[i] == 'A') {

             f[v] = find(u);

             tchange(u, sv);

             tchange(p[f[u]], -sv);

         } else {

             int s = query(ord[find(u)]);

             printf("%d\n", (s - sv) * sv);

         }

     }

     return ;

 }

 void tchange(int u, int x) {

     while (u != -) {

         change(ord[top[u]], x);

         change(ord[u] + , -x);

         u = p[top[u]];

     }

 }

 void dfs2(int u) {

     static int t;

     ord[u] = ++t;

     if (!son[u])

         return;

     top[son[u]] = top[u];

     dfs2(son[u]);

     for (edge* q = g[u]; q; q = q->next)

         if (p[q->v] == u && q->v != son[u]) {

             top[q->v] = q->v;

             dfs2(q->v);

         }

 }

 int low_bit(int k) {

     return k & -k;

 }

 void change(int k, int x) {

     for (; k <= n; k += low_bit(k))

         fw[k] += x;

 }

 int query(int k) {

     int ret = ;

     for (; k; k -= low_bit(k))

         ret += fw[k];

     return ret;

 }

 void dfs1(int u) {

     sum[u] = ;

     for (edge* q = g[u]; q; q = q->next)

         if (!p[q->v]) {

             p[q->v] = u;

             dfs1(q->v);

             sum[u] += sum[q->v];

             if (sum[son[u]] < sum[q->v])

                 son[u] = q->v;

         }

 }

 int find(int x) {

     return f[x] == x ? x : (f[x] = find(f[x]));

 }

 void add_edge(int u, int v) {

     static edge pool[N * ];

     static edge* p = pool;

     p->v = v;

     p->next = g[u];

     g[u] = p;

     ++p;

 }

在线做法：LCT

$LCT$ 由于使用 $splay$ 维护一条链，但 $splay$ 的中序遍历才是链从上往下的顺序，形态不一样（同一点在 $splay$ 的子树和在原树中的子树也不一样），所以 $splay$ 没法直接维护原树的子树信息。

但对于某些题来说，可以做一些“假的”维护子树信息。

对于这题，即使询问边的两端点 $x,y$ 是相邻的，我们也可以 $split$ 出 $x$ 到 $y$ 的只有一条边的路径。

这里复习一下 $split(x,y)$ 是干嘛来着。

首先 $makeroot(x)$，即 $x$ 成了其所在 $splay$ 的根，且它没有左子树。

然后 $access(y)$，由于 $x$ 和 $y$ 本来就相邻，那么两点间就连了条重边，两点连出的其余所有边都变成轻边。

最后 $splay(y)$，$y$ 成了这个 $splay$ 的根，$x$ 成了 $y$ 的左儿子且 $x$ 没有儿子。

也就是说，$split(x,y)$ 后，就成了这样子

那这俩点所在的 $splay$ 就只剩这 $2$ 个点了！（详见 $access$）

而且两点连出去的其它边都是轻边！

我们知道，轻边不是用 $splay$ 维护的，所以我们可以 $fake$ 一下，装作维护子树信息，其实是维护每个点的所有轻儿子的子树信息。

轻儿子的信息分这么几个部分维护：

1. 做某些操作时，对于一个点的所有儿子，一条边变重后，原来的重边变成轻边，所以这个点的轻子树大小总和 $lit$ 减去变重的儿子的 $size$，加上变轻的儿子的 $size$。

2. 加边时（$link(x,y)$），由于 $split(x,y)$，$y$ 会变成 $x$ 的父亲，且两点间连上重边，所以 $y$ 的 $lit$ 加上以 $x$ 为根的子树的 $size$。

3. $splay$ 做 $pushup$ 时别忘了把 $size$ 值加上其 $lit$。本来 $LCT$ 的 $splay$ 是不维护轻子树信息的，这里为了最后的查询，可以直接加上它们（比较方便）。

查询时，实际上就是查询 $x$ 的所有轻儿子的子树大小总和。由于 $x$ 没有重儿子，它的 $size$ 值实际上就是它本身和所有轻子树大小的总和，也就是 $x$ 这边的答案。

$y$ 那边的答案就是 $size_y-size_x$。

原来这类题还可以直接把 $size$ 加上轻儿子的信息……

最后说一个我做题时混淆了的概念：

如果连一条边会影响一端点及其所有祖先的信息（比如子树 $size$ 值，连边时就会影响点 $y$ 及其所有祖先），那 $link(x,y)$ 时不能只 $makeroot(x)$（把 $x$ 设成其所在的树的根，然后修改其父亲为 $y$，$y$ 的位置其实无所谓），而要 $split$ 出这两点的路径（也就是说要把 $y$ 转到整棵树根）。

因为 $LCT$ 只保证了每棵 $splay$ 的深度是 $log$ 级别的，没有保证整棵树的深度，也就是说如果不把 $y$ 设成根，把 $y$ 一直 $pushup$ 到整棵树的根等于做暴力，复杂度不对。

时间复杂度 $O(n+q\times log(n))$。

 #include<bits/stdc++.h>

 #define rep(i,x,y) for(int i=x;i<=y;++i)

 #define dwn(i,x,y) for(int i=x;i>=y;--i)

 #define ll long long

 #define N 100002

 using namespace std;

 inline int read(){

     int x=; bool f=; char c=getchar();

     for(;!isdigit(c);c=getchar()) if(c=='-') f=;

     for(; isdigit(c);c=getchar()) x=(x<<)+(x<<)+(c^'');

     if(f) return x;

     return -x;

 }

 int n,m,siz[N],son[N][],fa[N],lit[N]; //lit维护一个点的所有轻边连向的子树

 bool rev[N];

 namespace LCT{

     inline bool dir(int x){return son[fa[x]][]==x;}

     inline bool isroot(int x){return son[fa[x]][]!=x && son[fa[x]][]!=x;}

     inline void pushup(int x){siz[x]=siz[son[x][]]+siz[son[x][]]+lit[x]+;}

     inline void pushdown(int x){

         if(rev[x])

             swap(son[x][],son[x][]), rev[son[x][]]^=, rev[son[x][]]^=, rev[x]=;

     }

     inline void rotate(int x){

         int f,ff,k; f=fa[x],ff=fa[f],k=dir(x);

         fa[x]=ff; if(!isroot(f)) son[ff][dir(f)]=x;

         son[fa[son[x][k^]]=f][k] = son[x][k^];

         son[fa[f]=x][k^]=f;

         pushup(f), pushup(x);

     }

     inline void splay(int x){

         int sta[N],top,f;

         for(int i=x,top=;!isroot(i);i=fa[i]) sta[top--]=i;

         for(;top;pushdown(sta[--top]));

         for(f=fa[x];!isroot(x);rotate(x),f=fa[x])

             if(!isroot(f)) rotate(dir(f)==dir(x)?f:x);

     }

     inline void access(int x){

         for(int s=,f=x; f; s=f,f=fa[f]){

             splay(f);

             lit[f]+=siz[son[f][]]-siz[s]; //f与s间连上了重边，与原来f的重儿子（即splay中f的右儿子）连上了轻边，由于是维护轻子树信息，所以要加一个、减一个。

             //printf("%d %d %d\n",s,f,lit[f]);

             if(lit[f]<) printf("err\n");

             son[f][]=s, pushup(f);

         }

     }

     inline void makeroot(int x){access(x),splay(x),rev[x]^=;}

     inline void split(int x,int y){makeroot(x),access(y),splay(y);}

     inline void link(int x,int y){split(x,y),fa[x]=y; lit[y]+=siz[x],pushup(y);}

     inline ll query(int x,int y){split(x,y); return 1ll*siz[x]*(siz[y]-siz[x]);}

 }

 using namespace LCT;

 int main(){

     n=read(),m=read();

     rep(i,,n) siz[i]=;

     char opt[]; int x,y;

     rep(i,,m){

         scanf("%s",opt); x=read(),y=read();

         if(opt[]=='A') link(x,y);

         else printf("%lld\n",query(x,y));

     }

     return ;

 }

巴特西

【BJOI2014/bzoj4530】大融合

题意

题解

离线做法：树剖+树状数组/线段树

在线做法：LCT

最新文章

热门文章