洛谷P4220 [WC2018]通道（边分治+虚树）
2024-08-25 20:43:13
题面
题解
代码不就百来行么也不算很长丫
虽然这题随机化贪心就可以过而且速度和正解差不多不过我们还是要好好学正解
前置芝士
边分治
米娜应该都知道点分治是个什么东西，而边分治，顾名思义就是对边进行分治，即每次选出一条“子树中点的个数的最大值最小”的边，处理所有经过这条边的路径的贡献，然后割掉这条边之后对子树递归下去就好了
然而出题人给你一个菊花图就能把你卡得不要不要的
我们发现上述策略在一个二叉树上是最优的，因为割掉边之后左右子树大小都会变为原来的一半
于是这里就需要多叉树转二叉树，具体的流程可以看\(shadowice\)巨巨的图
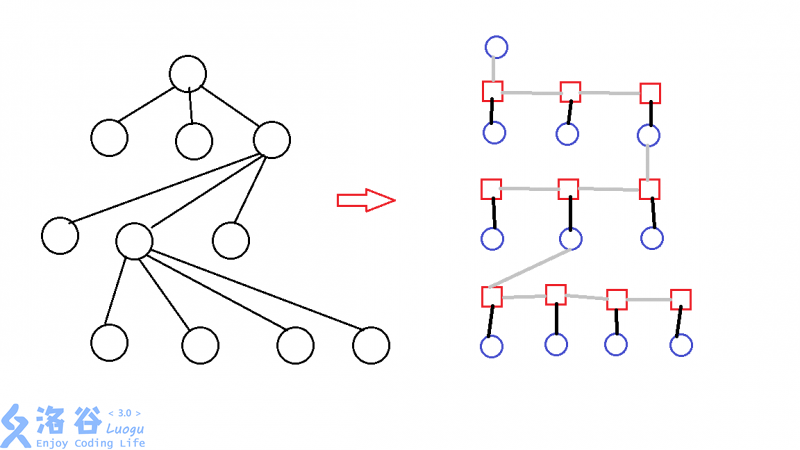
这样的话点数最多变成\(2n\)，但是分治的时候复杂度就有保证了
虚树
咱对这东西也不熟所以请米娜自己去找吧
本题
本题要求我们最大化
\[dis1(x,y)+dis2(x,y)+dis3(x,y)
\]
\]
我们在第一棵树上边分，处理所有经过\((u,v)\)这条边的路径的贡献，那么肯定满足\(x\)和\(u\)在同一联通块（以下称为黑点），\(y\)和\(v\)在同一个联通块（以下称为白点），并且因为\((u,v)\)的长度是一个定值，那么我们需要最大化
\[dis1(x,u)+dis1(v,y)+dis2(x,y)+dis3(x,y)
\]
\]
把它改写一下
\[dis1(x,u)+dis1(v,y)+dep2(x)+dep2(y)+dep3(x)+dep3(y)
\]
\]
上面的柿子里是只和\(x,y\)有关的，那么我们还需要减去
\[2\times dep2(LCA2(x,y))+2\times dep3(LCA3(x,y))
\]
\]
因为我们已经选定了\(u,v\)，所以我们可以快速预处理出\(w(x)=dis1(x,u/v)+dep2(x)+dep3(x)\)，那么就变成最大化
\[w(x)+w(y)-2\times dep2(LCA2(x,y))-2\times dep3(LCA3(x,y))
\]
\]
发现每一次分治的时候满足条件的\(x,y\)都是一个点集，那么我们可以把这些点集放到第二颗树上做一个虚树
在虚树上，我们可以枚举\(LCA\)，设为\(p\)，那么此时\(dep2(LCA2(x,y))\)就是个定值了，我们需要求出两个点\(x,y\)，其中\(x\)是黑点，\(y\)是白点，且\(x,y\)不在\(p\)的同一子树内，并且最大化
\[w(x)+w(y)-2\times dep3(LCA3(x,y))
\]
\]
首先你需要知道一个结论：如果有一棵树\(T\)，边权非负，直径的端点为\(u,v\)，和一棵树\(G\)，直径的端点为\(a,b\)，那么用一条边将它们连接起来之后（无论把两棵树的那两个节点相连），直径一定为\(uv,ua,ub,va,vb,ab\)六条路径中的一条（这里的直径定义为不存在路径比它长，不过有可能有路径和它长度相等）
证明的话可以感性理解一下
然后这里就需要用到一个推论：对于两个树上的点集\(A,B\)，\(A\)的直径端点为\(u,v\)，\(B\)的直径端点为\(a,b\)，那么一条左右端点分别在\(A,B\)中的最长的路径必为\(ua,uv,va,vb\)四条路径中的一条
然而放到这里有什么用么？\(w(x)+w(y)-2\times dep3(LCA3(x,y))\)怎么看也不像是树上两点的距离啊？
那么我们把它化一下，变成
\[dis1(x,u)+dep2(x)+dis2(y,v)+dep2(y)+dis3(x,y)
\]
\]
那么我们可以看做是在第三棵树上，在\(x\)下面挂一个虚点\(x'\)，\((x,x')\)的长度为\(dis1(x,u)+dep2(x)\)，\(y\)同理，这样能看做是树上的一条路径了，也就是说我们关于树上路径的那个结论成立
然后就没有然后了，码吧
似乎有大佬写了随机化贪心的做法，这里说一下好了，就是每一次枚举根节点算出三棵树上其他点到它距离总和的最大值，用距离最大的点来更新根节点，然后每隔几次之后重新\(rand\)根节点……我调了调之后速度已经和我的正解差不多了（虽然会被\(uoj\)上的\(hack\)数据卡掉不过比赛的时候可没有这么强的数据啊）
虽然我估计考场上我可能这种随机化贪心都打不出来
可以对比一下下面两份代码的码量……
这份是随机化贪心，洛谷上能过，\(uoj\)会被\(hack\)
// luogu-judger-enable-o2
//minamoto
#include<bits/stdc++.h>
#define R register
#define ll long long
#define CL 1000.0*clock()/CLOCKS_PER_SEC
#define fp(i,a,b) for(R int i=(a),I=(b)+1;i<I;++i)
#define fd(i,a,b) for(R int i=(a),I=(b)-1;i>I;--i)
#define go(u) for(int i=head[u],v=e[i].v;i;i=e[i].nx,v=e[i].v)
template<class T>inline bool cmax(T&a,const T&b){return a<b?a=b,1:0;}
using namespace std;
char buf[1<<21],*p1=buf,*p2=buf;
inline char getc(){return p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++;}
ll read(){
R ll res,f=1;R char ch;
while((ch=getc())>'9'||ch<'0')(ch=='-')&&(f=-1);
for(res=ch-'0';(ch=getc())>='0'&&ch<='9';res=res*10+ch-'0');
return res*f;
}
const int N=1e5+5;
struct eg{int v,nx;ll w;};
struct Gr{
eg e[N<<1];int head[N],tot;
inline void add(R int u,R int v,R ll w){e[++tot]={v,head[u],w},head[u]=tot;}
ll dis[N];
void dfs(int u,int fa){go(u)v!=fa?(dis[v]=dis[u]+e[i].w,dfs(v,u),0):0;}
}g[3];
ll res,w,las;bool vis[N];int n,u,v,c;
inline int rd(){return 1ll*rand()*rand()%n+1;}
void qwq(){
fp(rt,1,n){
g[0].dis[rt]=g[1].dis[rt]=g[2].dis[rt]=0;
g[0].dfs(rt,0),g[1].dfs(rt,0),g[2].dfs(rt,0);
fp(j,1,n)cmax(res,g[0].dis[j]+g[1].dis[j]+g[2].dis[j]);
}
printf("%lld\n",res);
}
int main(){
srand(19260817);
// freopen("testdata.in","r",stdin);
double st=CL;
n=read();
fp(i,1,n-1)u=read(),v=read(),w=read(),g[0].add(u,v,w),g[0].add(v,u,w);
fp(i,1,n-1)u=read(),v=read(),w=read(),g[1].add(u,v,w),g[1].add(v,u,w);
fp(i,1,n-1)u=read(),v=read(),w=read(),g[2].add(u,v,w),g[2].add(v,u,w);
if(n<=3500)return qwq(),0;
while(CL-st<=3400){
int rt=rd();las=res;
while(vis[rt])rt=rd();
fp(i,1,5){
if(vis[rt])break;
vis[rt]=1,g[0].dis[rt]=g[1].dis[rt]=g[2].dis[rt]=0;
g[0].dfs(rt,0),g[1].dfs(rt,0),g[2].dfs(rt,0);
ll mx=0;
fp(j,1,n)
cmax(res,g[0].dis[j]+g[1].dis[j]+g[2].dis[j]),
!vis[j]&&cmax(mx,g[0].dis[j]+g[1].dis[j]+g[2].dis[j])?rt=j:0;
}
las==res?++c:c=0;
if(c>=20)break;
}
printf("%lld\n",res);
return 0;
}
然后下面这份是正解
虽然它们都说求\(LCA\)要用\(ST\)表然而亲测用树剖似乎速度差不多？
// luogu-judger-enable-o2
//minamoto
#include<bits/stdc++.h>
#define R register
#define ll long long
#define fp(i,a,b) for(R int i=(a),I=(b)+1;i<I;++i)
#define fd(i,a,b) for(R int i=(a),I=(b)-1;i>I;--i)
#define go(u) for(int i=head[u],v=e[i].v;i;i=e[i].nx,v=e[i].v)
template<class T>inline bool cmax(T&a,const T&b){return a<b?a=b,1:0;}
template<class T>inline bool cmin(T&a,const T&b){return a>b?a=b,1:0;}
using namespace std;
char buf[1<<21],*p1=buf,*p2=buf;
inline char getc(){return p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++;}
ll read(){
R ll res,f=1;R char ch;
while((ch=getc())>'9'||ch<'0')(ch=='-')&&(f=-1);
for(res=ch-'0';(ch=getc())>='0'&&ch<='9';res=res*10+ch-'0');
return res*f;
}
const int N=5e5+5;
int lg[N],s[2][N],top[2],ty[N];ll w[N],res;
int n;
namespace tree3{
struct eg{int v,nx;ll w;}e[N<<1];int head[N],tot;
inline void add(R int u,R int v,R ll w){e[++tot]={v,head[u],w},head[u]=tot;}
int top[N],dep[N],fa[N],sz[N],son[N];ll dis[N];
void dfs1(int u){
sz[u]=1,dep[u]=dep[fa[u]]+1;
go(u)if(v!=fa[u]){
dis[v]=dis[u]+e[i].w,fa[v]=u,dfs1(v),sz[u]+=sz[v];
sz[v]>sz[son[u]]?son[u]=v:0;
}
}
void dfs2(int u,int t){
top[u]=t;if(!son[u])return;
dfs2(son[u],t);
go(u)!top[v]?(dfs2(v,v),0):0;
}
inline int LCA(R int u,R int v){
while(top[u]!=top[v]){
dep[top[u]]<dep[top[v]]?(swap(u,v),0):0;
u=fa[top[u]];
}return dep[u]<dep[v]?u:v;
}
inline ll Dis(R int u,R int v){return w[u]+w[v]+dis[u]+dis[v]-(dis[LCA(u,v)]<<1);}
}
namespace tree2{
struct eg{int v,nx;ll w;}e[N<<1];int head[N],tot;
inline void add(R int u,R int v,R ll w){e[++tot]={v,head[u],w},head[u]=tot;}
int top[N],dep[N],fa[N],sz[N],son[N],low[N],dfn[N],cnt;ll dis[N];
void dfs1(int u){
sz[u]=1,dep[u]=dep[fa[u]]+1,dfn[u]=++cnt;
go(u)if(v!=fa[u]){
dis[v]=dis[u]+e[i].w,fa[v]=u,dfs1(v),sz[u]+=sz[v];
sz[v]>sz[son[u]]?son[u]=v:0;
}
low[u]=cnt;
}
void dfs2(int u,int t){
top[u]=t;if(!son[u])return;
dfs2(son[u],t);
go(u)!top[v]?(dfs2(v,v),0):0;
}
inline int LCA(R int u,R int v){
while(top[u]!=top[v]){
dep[top[u]]<dep[top[v]]?(swap(u,v),0):0;
u=fa[top[u]];
}return dep[u]<dep[v]?u:v;
}
inline void Pre(){fp(i,1,n)head[i]=0;tot=0;}
struct node{
int u,v;ll d;
node():u(0),v(0),d(0){}
node(R int uu,R int vv,R ll dd):u(uu),v(vv),d(dd){}
node(R int uu,R int vv):u(uu),v(vv){d=tree3::Dis(u,v);}
inline bool operator <(const node &b)const{return !u?1:!b.u?0:d<b.d;}
inline node operator +(const node &b)const{
node res=max(*this,b);
cmax(res,max(node(u,b.u),node(u,b.v))),
cmax(res,max(node(v,b.u),node(v,b.v)));
return res;
}
inline ll merge(const node &b){
return max(max(node(u,b.u),node(u,b.v)),max(node(v,b.u),node(v,b.v))).d;
}
}f[N][2];
int q[N<<2],stack[N<<1],t;bool vis[N],ins[N];ll tag;
inline bool cmp(const int &x,const int &y){return dfn[x]<dfn[y];}
void dp(int u){
f[u][0]=f[u][1]=node();
vis[u]?(f[u][ty[u]]=node(u,u,0),0):0;
go(u){
dp(v),
cmax(res,max(f[u][0].merge(f[v][1]),f[u][1].merge(f[v][0]))+tag-(dis[u]<<1)),
f[u][0]=f[u][0]+f[v][0],
f[u][1]=f[u][1]+f[v][1];
}
}
void solve(ll val){
tag=val,t=0,tot=0;
fp(i,1,::top[0])q[++t]=s[0][i];
fp(i,1,::top[1])q[++t]=s[1][i];
sort(q+1,q+1+t,cmp);
fp(i,1,t)vis[q[i]]=ins[q[i]]=1,w[q[i]]+=dis[q[i]];
for(R int i=t,lca;i>1;--i)lca=LCA(q[i],q[i-1]),!ins[lca]?(q[++t]=lca,ins[lca]=1):0;
sort(q+1,q+1+t,cmp);
for(R int i=1,top=0;i<=t;++i){
while(top&&low[stack[top]]<dfn[q[i]])--top;
if(top)add(stack[top],q[i],dis[q[i]]-dis[stack[top]]);
stack[++top]=q[i];
}
dp(q[1]);
fp(i,1,t)vis[q[i]]?w[q[i]]-=dis[q[i]]:0,vis[q[i]]=ins[q[i]]=head[q[i]]=0;
}
}
namespace tree1{
struct eg{int v,nx;ll w;}e[N<<2];int head[N<<1],tot=1;
inline void add(R int u,R int v,R ll w){e[++tot]={v,head[u],w},head[u]=tot;}
int cnt;
namespace qwq{
struct eg{int v,nx;ll w;}e[N<<1];int head[N],las[N],tot;
inline void add(R int u,R int v,R ll w){e[++tot]={v,head[u],w},head[u]=tot;}
void ins(int u,int v,ll w){
++cnt,tree1::add(cnt,v,w),tree1::add(v,cnt,w),
tree1::add(las[u],cnt,0),tree1::add(cnt,las[u],0),
las[u]=cnt;
}
void build(int u,int fa){go(u)if(v!=fa)ins(u,v,e[i].w),build(v,u);}
inline void init(){fp(i,1,n)las[i]=i;cnt=n;build(1,0);}
}
bool vis[N];int sz[N],rt,mx;ll dis[N];
void findrt(int u,int fa,int size){
sz[u]=1;
go(u)if(!vis[i>>1]&&v!=fa){
findrt(v,u,size),sz[u]+=sz[v];
cmin(mx,max(sz[v],size-sz[v]))?rt=i:0;
}
}
void dfs(int u,int fa,int op){
u<=n?ty[u]=op,s[op][++top[op]]=u:0;
go(u)if(v!=fa&&!vis[i>>1])
dis[v]=dis[u]+e[i].w,dfs(v,u,op);
}
void solve(int u,int size){
mx=1e9,findrt(u,0,size);
if(mx==1e9)return;
vis[rt>>1]=1;
int nw=rt,ss=size-sz[e[rt].v];
top[0]=top[1]=dis[e[rt].v]=dis[e[rt^1].v]=0;
dfs(e[rt].v,0,1),dfs(e[rt^1].v,0,0);
fp(i,1,top[0])w[s[0][i]]+=dis[s[0][i]];
fp(i,1,top[1])w[s[1][i]]+=dis[s[1][i]];
tree2::solve(e[rt].w);
fp(i,1,top[0])w[s[0][i]]-=dis[s[0][i]];
fp(i,1,top[1])w[s[1][i]]-=dis[s[1][i]];
solve(e[nw].v,sz[e[nw].v]),solve(e[nw^1].v,ss);
}
}
int main(){
// freopen("testdata.in","r",stdin);
n=read();
fp(i,2,n+n)lg[i]=lg[i>>1]+1;
int u,v;ll w;
fp(i,1,n-1)u=read(),v=read(),w=read(),tree1::qwq::add(u,v,w),tree1::qwq::add(v,u,w);
fp(i,1,n-1)u=read(),v=read(),w=read(),tree2::add(u,v,w),tree2::add(v,u,w);
fp(i,1,n-1)u=read(),v=read(),w=read(),tree3::add(u,v,w),tree3::add(v,u,w);
tree2::dfs1(1),tree2::dfs2(1,1),tree2::Pre(),
tree3::dfs1(1),tree3::dfs2(1,1);
tree1::qwq::init(),tree1::solve(1,tree1::cnt);
printf("%lld\n",res);
return 0;
}
最新文章
- 在脚本中使用sudo命令，将密码保存在脚本中，不需要手动输入密码
- Amd64 and Va_arg
- 移动web开发，12个触摸及多点触摸事件常用Js插件
- HDU 5128 The E-pang Palace(2014广州赛区现场赛B题 计算几何)
- springmvc学习笔记--Interceptor机制和实践
- SAPScript、Smartforms动态打印图像或者背景图片
- Linux下memcache的安装和启动(转)
- pjsip视频通信开发(上层应用)之数字键盘的制作
- 沈逸老师ubuntu速学笔记（1）--安装flashplayer，配置中文输入法以及常用命令
- Nodejs异步流程控制Async
- JS之对象数组遍历？
- android anim 动画效果
- 呈现怎样的香蕉饼路线Android系统
- Lucene搜索引擎例子demo
- python中sorted()和set()去重，排序
- thymeleaf资源加载问题（从Controller跳转）
- 【★★★★★】提高PHP代码质量的36个技巧
- URL传值乱码
- 有关于一次windows权限方面的一次学习
- 关于C++中操作符重载的疑问 ：四个运算符=, -&gt;, [], ()不可以重载为全局函数（友员函数）