CROI R1

$CROI$ $R1$

　　今天参加了一场比赛，什么比赛呢？CROI。

　　CROI是什么呢? $Challestend$ $Rehtorbegnaro$ $OI$。总的来说就是我们机房的一些神仙出的题啦。

　　这篇文章没有密码...被你发现啦!

　　T1：Challestend and Hyperrectangle

　　一道特别神仙的题目。

　　题意概述一下：给出一个高维立方体的 $n$ 个边长，将它的表面刷上漆，再将它切成单位小块，求恰好有 $i$ 面被着色的小立方体个数，对998244353取模.$i \in [0,2n]$，$4<=n<=30000,1<=a_i<=2^{64}$.

　　不会做呀...本来是有一点想法的，就是从一二三维的简单情况开始，进行类比，推出来一个比较科学的式子（它甚至可以过一个比较大的样例），但是对于 $a<=2$ 的情况就会崩溃，而且小一点的数据里每个都有这种情况，所以最后也没有分了。还是讲一下思路：

　　一维：两个顶点，$a-2$个无色立方体；

　　二维：四个顶点，$2\times(a-2+b-2)$个棱上的点,$(a-2)(b-2)$个无色立方体；

　　三维：八个顶点，$4\times(a-2+b-2+c-2)$个棱上的点，$2\times((a-2)(b-2)+(a-2)(c-2)+(b-2)(c-2))$个面上的点，$(a-2)(b-2)(c-2)$个无色的；

　　一维二维的可能比较难想，在这里放个图：

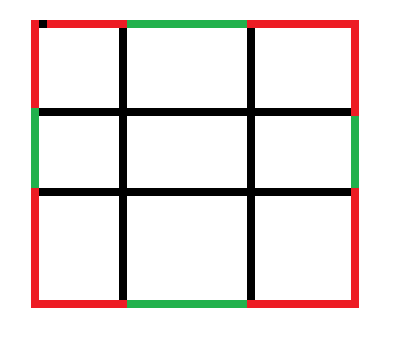
　　这题比较玄学的一点就是怎么分辨 $n$ 维立方体的“面”,因为按照一般的思路来说，只有三维立方体才有“面”。不过通过看样例，可以发现这道题里的“面”指的就是 $n-1$ 维的空间啦。

　　T2：Challestend and Anarchy Heap

　　这道题还是比较简单的（虽然我没做出来）。

　　题意概述：将斐波那契数顺次插入一个二叉堆，比较函数是随机的，问每次插入后堆顶的期望值的和,对998244353取模。$T<=400,1<=n<2^{64}$

　　期望具有线性性，所以只要算出每个点作为堆顶的概率。虽然比较函数坏掉了，但是树的形态还是固定的。可以发现每次插入新数后，堆顶要么是新数，要么不变。考虑是新数的概率：新数运气超好，一路随机上来到了根，也就是$\frac{1}{2^{x}}$，(x=当前点离根节点的距离)，其它情况下都继承原答案。递推可以做到 $O(N)$，但是显然跑不过，所以可以矩乘，由于深度不固定，还得分段矩乘，有一点难写。

　　T3：Challestend and Summation

　　挺好的一道题，专治多项式学傻。

　　对以下式子求值：$n<=1e7,m<=1000$,F是一个 $m$ 项多项式。

　　$\sum_{i=1}^n\sum_{j|i}F(j) \space (\%998244353)$

　　首先给大家表演一下多项式学傻的人的做法：

　　$\sum_{j=1}^n\frac{n}{j}\sum_{i=0}^{m-1}a_ij^i$

　　$\sum_{j=1}^n\frac{n}{j}\sum_{i=0}^{m-1}a_i\sum_{k=1}^jS(i,k)\binom{j}{k}k!$

　　$\sum_{j=1}^n\frac{n}{j}\sum_{i=0}^{m-1}a_i\sum_{k=1}^jS(i,k)\frac{j!}{k!(j-k)!}k!$

　　$\sum_{j=1}^n\frac{n}{j}\sum_{i=0}^{m-1}a_i\sum_{k=1}^mS(i,k)\frac{j!}{(j-k)!}$

　　$\sum_{i=0}^{m-1}a_i\sum_{k=1}^mS(i,k)\sum_{j=1}^n\frac{n}{j}\frac{j!}{(j-k)!}$

　　第二类斯特林太妙啦，可以将很大的幂指数换成好求很多的阶乘！没错我当时就是这么想的。

　　后来又想了一下才发现...画到第一步时已经是一个很显然的整除分块形式，只要能快速求出 $f$ 的前缀和即可。而通过一些函数知识可以得到，$m$ 次函数的前缀和是一个 $m+1$ 次的函数，所以插值即可。注意这里不能写 $m^2$ 的插值，要优化一下到 $m$.

 # include <cstdio>

 # include <iostream>

 # define R register int

 # define ll long long

 using namespace std;

 const int mod=;

 const int maxn=;

 int n,m,a[maxn],k;

 int ans,sx[maxn],f[maxn],inv[maxn],x[maxn],y[maxn];

 ll cal (ll x)

 {

     ll s=,ans=;

     for (R i=;i<m;++i)

     {

         ans=(ans+1LL*a[i]*s)%mod;

         s=s*x%mod;

     }

     return ans;

 }

 ll qui (ll a,ll b)

 {

     ll s=;

     while(b)

     {

         if(b&) s=s*a%mod;

         a=a*a%mod;

         b>>=;

     }

     return s;

 }

 ll S (int v)

 {

     if(v<=m) return y[v];

     ll ans=;

     for (R i=;i<=m;++i)

         ans=(ans+1LL*y[i]*sx[i]%mod*(1LL*f[v]*inv[v-i]%mod*f[v-i-]%mod*inv[v--m]%mod))%mod;

     return ans;

 }

 int main()

 {

     scanf("%d%d",&n,&m); k=m;

     for (R i=;i<m;++i) scanf("%d",&a[i]);

     for (R i=;i<=m;++i)

     {

         x[i]=i;

         y[i]=cal(i);

         y[i]=(y[i]+y[i-])%mod;

     }

     f[]=;

     for (R i=;i<=n;++i) f[i]=1LL*f[i-]*i%mod;

     inv[n]=qui(f[n],mod-);

     for (R i=n;i>=;--i) inv[i-]=1LL*inv[i]*i%mod;

     for (R i=;i<=k;++i)

     {

         sx[i]=;

         for (R j=;j<=k;++j)

         {

             if(i==j) continue;

             sx[i]=1LL*sx[i]*(x[i]-x[j]+mod)%mod;

         }

         sx[i]=qui(sx[i],mod-);

     }

     int l=,r;

     while(l<=n)

     {

         r=n/(n/l);

         ans=(ans+1LL*(n/l)*((S(r)-S(l-))%mod+mod)%mod)%mod;

         l=r+;

     }

     printf("%d\n",ans);

     return ;

 }

　　T4:Challestend and the Second War against Duliu

　　一看题目就可以发现这道题“Duliu”的本质了。

　　简单的说：给定一个长度为 $n$ 的数列以及 $n$ 个观察者，每个观察者可以看到 $[l_i,r_i]$ 的一段区域，要求支持如下操作：

　　对数列区间加；查询一段编号连续的观察者所能看到的值的和；修改某个观察者的观察区域。

　　$n,m<=10^5$

　　这题能做？$O(N\sqrt{N}logN)$ 的做法其实不是特别难想，但是似乎会被卡常。另注：这题的最大难点在于读题。

　　刚刚听了题解，感觉学到了很多东西，原来分块可以做到 $O(\sqrt{N})$ 区间加，$O(1)$ 区间查询，实在是非常神奇。

　　那么这里先写抄一份正常解法：

　　首先考虑分块维护区间和，有一个比较巧妙的做法是对于每个块维护和，再对于每个点维护块内的前后缀和，这样就可以做到 $O(1)$ 区间查询了。如果直接把这个做法扩展到区间加上复杂度就崩了，因为每次要打很多的标记。考虑对于每个块维护一个delta，表示未下放的标记...但是每个点得到的标记的实际值和它的位置是有关的，所以这里有两个做法：1.差分；2.delta标记变为维护一个等差数列的首项和公差；再用这种巧妙的分块代替原先的树状数组，即可通过本题 $O(N\sqrt{N})$

　　下面是我的乱搞做法：

　　对于观察者序列分块，每个块内维护一个长度为 $n$ 的数组，每个位置上的值表示这个块内的观察者有多少能看到这个位置。修改时，对于每个块计算贡献；查询时，整块可以直接得到答案，散点暴力查询。修改观察区间则更简单，只需要在相应的块内做一些处理就可以了。这里需要一个区间修改的数据结构，选择树状数组。

　　这样做的问题在于每个操作之间的复杂度过于不平衡，所以用 a,b,c 表示三个操作的操作次数，m表示分块大小，得到下式：

　　$a\frac{N}{M}logN+b\frac{N}{M}+bMlogN+clogN$

　　这样就可以用...模拟退火得到最优的块大小！

　　---shzr

巴特西

CROI R1

最新文章

热门文章