Binary Search-使用二叉搜索树
终于到二叉树了,每次面试时最担心面试官问题这块的算法问题,所以接下来就要好好攻克它~
关于二叉树的定义网上一大堆,这篇做为二叉树的开端,先了解一下基本概念,直接从网上抄袭:
先了解下树的概念,balabala~~:


更通俗的定义:

而二叉树就是树结构的一个经典树,也是要讨论的主题,下面再来看下二叉树的定义:


而用二叉树主要是用来干嘛呢?上次不是学习过了一个利用递归实现折半查找的算法(http://www.cnblogs.com/webor2006/p/7182756.html)么?而当时实现的前提是数列一定得有序,那如果数列是无序的,但是也想对它进行搜索,那就可以给它创建一个结构:二叉搜索树,它是二叉树的一种,那它的具体定义是怎么样的?
这里从两个围度来理解:
1、如何构建一个二叉搜索树?
给出一组元素:【5、8、3、4、1、7、6】,构建过程如下:
第一步:将第一个元素【5】做为根结点:
第二步:把第二个元素【8】拿出来与第一个元素做比较,如果比根节点大就放在右边,如果比根节点小就放在左边,由于8>5,则放在5的右边,如下:

第三步:同样的道理 拿出来第三个元素【3】再与根节点进行比较,结果如下:

第四步:上一步已经把二叉树的第二层填满了,接下来的元素【4】首先要与根节点进行比较,再与子树的节点进行比较,如下:

第五步:按照以上的方式,把接下来的元素依次插入到树中即可,下面是剩下元素的整个构建过程:


2、如何从二叉搜索树中查找一个元素?
比如搜“7”这个元素:
1、拿7跟根结点5比,比它大,则搜5的右节点,左节点抛弃;
2、拿7跟8比,比它小,所以必然是在8的左子孙里面,刚好就搜到了。
比如搜“2”这个元素:
1、拿2跟根结点5比,比它小,则搜5的左节点,右节点抛弃;
2、拿2跟3比,比它小,则搜3的左节点,右节点抛弃;
3、拿2跟1比,比它大,则需要转到1的右子孙里找,但是1没有右子孙所以2没有在这个树中,也就是未找到。
有了上面的思路之后,下面来看下具体代码实现,为了方便这里采用JAVA实现:
第一步:构建一个二叉搜索树:
public class BinarySearchTree {
TreeNode root = null;
class TreeNode{
int value;
int position;
TreeNode left = null, right = null;
TreeNode(int value, int position){
this.value = value;
this.position = position;
}
}
public void add(int value, int position){
if(root == null){//生成一个根结点
root = new TreeNode(value, position);
} else {
//生成叶子结点
add(value, position, root);
}
}
private void add(int value, int position, TreeNode node){
if(node == null)
throw new RuntimeException("treenode cannot be null");
if(node.value == value)
return; //ignore the duplicated value
if(value < node.value){
if(node.left == null){
node.left = new TreeNode(value, position);
}else{
add(value, position, node.left);
}
}else{
if(node.right == null){
node.right = new TreeNode(value, position);
}else{
add(value, position, node.right);
}
}
}
//打印构建的二叉搜索树
static void printTreeNode(TreeNode node) {
if(node == null)
return;
System.out.println("node:" + node.value);
if(node.left != null) {
printTreeNode(node.left);
}
if(node.right != null) {
printTreeNode(node.right);
}
}
public static void main(String[] args) {
BinarySearchTree bst = new BinarySearchTree();
int a[] = { 5, 8, 3, 4, 1, 7, 6};
for(int i = 0; i < a.length; i++){
bst.add(a[i], i);
}
printTreeNode(bst.root);
}
}
编译运行:

刚好跟之前分析结果一样:

下面分析下具体构造流程:

Loop1: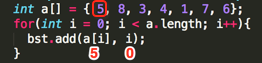
其第一个add(int value, int position)的参数为:value=5、position=0;
①、 ,判断root结点是否为null,条件为真,执行循环体:root = TreeNode(5, 0);
,判断root结点是否为null,条件为真,执行循环体:root = TreeNode(5, 0);
#######################################################################
Loop2: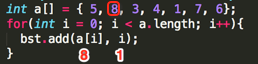
其第一个add(int value, int position)的参数为:value=8、position=1;
①、 ,判断root结点是否为null,条件为假,执行②;
,判断root结点是否为null,条件为假,执行②;
②、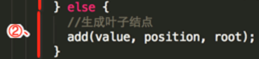 ,调用第二个add(int value, int position, TreeNode node)方法:add(8, 1, root=TreeNode(5, 0));
,调用第二个add(int value, int position, TreeNode node)方法:add(8, 1, root=TreeNode(5, 0));
③、 ,其条件为假,继续执行④;
,其条件为假,继续执行④;
④、 ,其中要添加的元素在二叉树中木有重复,也就是得保证二叉树中不可能有相同的元素条件为假,继续⑤;
,其中要添加的元素在二叉树中木有重复,也就是得保证二叉树中不可能有相同的元素条件为假,继续⑤;
⑤、 ,判断要插入的值是否比指定的结点小,8 < 5 为假,继续⑥
,判断要插入的值是否比指定的结点小,8 < 5 为假,继续⑥
⑥、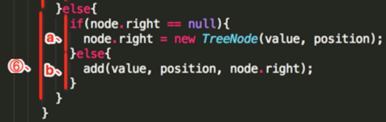
a、判断右接点是否为空,条件为真,于是乎直接生成右接点:node.right = TreeNode(8, 1)
所以此时的二叉树结果如下: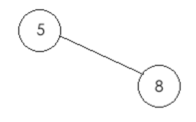
#######################################################################
Loop3: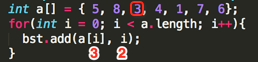
其第一个add(int value, int position)的参数为:value=3、position=2;
①、 ,判断root结点是否为null,条件为假,执行②;
,判断root结点是否为null,条件为假,执行②;
②、 ,调用第二个add(int value, int position, TreeNode node)方法:add(3, 2, root=TreeNode(5, 0));
,调用第二个add(int value, int position, TreeNode node)方法:add(3, 2, root=TreeNode(5, 0));
③、 ,其条件为假,继续执行④;
,其条件为假,继续执行④;
④、 ,其中要添加的元素在二叉树中木有重复,也就是得保证二叉树中不可能有相同的元素条件为假,继续⑤;
,其中要添加的元素在二叉树中木有重复,也就是得保证二叉树中不可能有相同的元素条件为假,继续⑤;
⑤、 ,判断要插入的值是否比指定的结点小,3 < 5 为真,执行条件体:
,判断要插入的值是否比指定的结点小,3 < 5 为真,执行条件体:
a、判断左接点是否为空,条件为真,于是乎直接生成左接点:node.left = TreeNode(3, 2)
所以此时的二叉树结果如下:
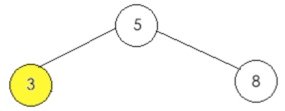
#######################################################################
Loop4: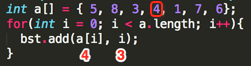
其第一个add(int value, int position)的参数为:value=4、position=3;
①、 ,判断root结点是否为null,条件为假,执行②;
,判断root结点是否为null,条件为假,执行②;
②、 ,调用第二个add(int value, int position, TreeNode node)方法:add(4, 3, root=TreeNode(5, 0));
,调用第二个add(int value, int position, TreeNode node)方法:add(4, 3, root=TreeNode(5, 0));
③、 ,其条件为假,继续执行④;
,其条件为假,继续执行④;
④、 ,其中要添加的元素在二叉树中木有重复,也就是得保证二叉树中不可能有相同的元素条件为假,继续⑤;
,其中要添加的元素在二叉树中木有重复,也就是得保证二叉树中不可能有相同的元素条件为假,继续⑤;
⑤、 ,判断要插入的值是否比指定的结点小,4 < 5 为真,执行条件体:
,判断要插入的值是否比指定的结点小,4 < 5 为真,执行条件体:
a、判断左接点是否为空,条件为假,执行b;
b、add(4, 3, node.left=(3, 2));继续递归:
b③、 ,其条件为假,继续执行④;
,其条件为假,继续执行④;
b④、 ,其中要添加的元素在二叉树中木有重复,也就是得保证二叉树中不可能有相同的元素条件为假,继续⑤;
,其中要添加的元素在二叉树中木有重复,也就是得保证二叉树中不可能有相同的元素条件为假,继续⑤;
b⑤、 ,判断要插入的值是否比指定的结点小,4 < 3 为假,继续执行⑥;
,判断要插入的值是否比指定的结点小,4 < 3 为假,继续执行⑥;
b⑥、
a、判断右接点是否为空,条件为真,于是乎直接生成右接点:node.right = TreeNode(4, 3)
所以此时的二叉树结果如下:
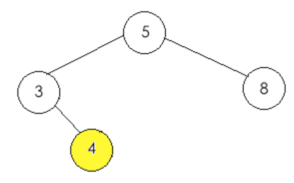
#######################################################################
Loop5: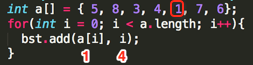
其第一个add(int value, int position)的参数为:value=1、position=4;
①、 ,判断root结点是否为null,条件为假,执行②;
,判断root结点是否为null,条件为假,执行②;
②、 ,调用第二个add(int value, int position, TreeNode node)方法:add(1, 4, root=TreeNode(5, 0));
,调用第二个add(int value, int position, TreeNode node)方法:add(1, 4, root=TreeNode(5, 0));
③、 ,其条件为假,继续执行④;
,其条件为假,继续执行④;
④、 ,其中要添加的元素在二叉树中木有重复,也就是得保证二叉树中不可能有相同的元素条件为假,继续⑤;
,其中要添加的元素在二叉树中木有重复,也就是得保证二叉树中不可能有相同的元素条件为假,继续⑤;
⑤、 ,判断要插入的值是否比指定的结点小,1 < 5 为真,执行条件体:
,判断要插入的值是否比指定的结点小,1 < 5 为真,执行条件体:
a、判断左接点是否为空,条件为假,执行b;
b、add(1, 5, node.left=(3, 2));继续递归:
b③、 ,其条件为假,继续执行④;
,其条件为假,继续执行④;
b④、 ,其中要添加的元素在二叉树中木有重复,也就是得保证二叉树中不可能有相同的元素条件为假,继续⑤;
,其中要添加的元素在二叉树中木有重复,也就是得保证二叉树中不可能有相同的元素条件为假,继续⑤;
b⑤、 ,判断要插入的值是否比指定的结点小,1 < 3 为真,执行循环体;
,判断要插入的值是否比指定的结点小,1 < 3 为真,执行循环体;
a、判断左接点是否为空,条件为真,于是乎直接生成左接点:node.left = TreeNode(1, 4)
所以此时的二叉树结果如下:
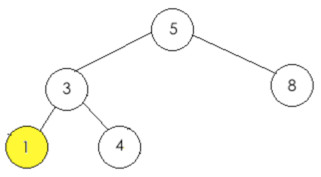
#######################################################################
Loop6: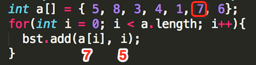
其第一个add(int value, int position)的参数为:value=7、position=5;
①、 ,判断root结点是否为null,条件为假,执行②;
,判断root结点是否为null,条件为假,执行②;
②、 ,调用第二个add(int value, int position, TreeNode node)方法:add(7, 5, root=TreeNode(5, 0));
,调用第二个add(int value, int position, TreeNode node)方法:add(7, 5, root=TreeNode(5, 0));
③、 ,其条件为假,继续执行④;
,其条件为假,继续执行④;
④、 ,其中要添加的元素在二叉树中木有重复,也就是得保证二叉树中不可能有相同的元素条件为假,继续⑤;
,其中要添加的元素在二叉树中木有重复,也就是得保证二叉树中不可能有相同的元素条件为假,继续⑤;
⑤、 ,判断要插入的值是否比指定的结点小,7 < 5 为假,继续执行⑥:
,判断要插入的值是否比指定的结点小,7 < 5 为假,继续执行⑥:
⑥、
a、判断右接点是否为空,条件为假,于是执行b;
b、add(7, 5, node.right=(8, 1));继续递归:
b③、 ,其条件为假,继续执行④;
,其条件为假,继续执行④;
b④、 ,其中要添加的元素在二叉树中木有重复,也就是得保证二叉树中不可能有相同的元素条件为假,继续⑤;
,其中要添加的元素在二叉树中木有重复,也就是得保证二叉树中不可能有相同的元素条件为假,继续⑤;
b⑤、 ,判断要插入的值是否比指定的结点小,7 < 8 为真,执行循环体;
,判断要插入的值是否比指定的结点小,7 < 8 为真,执行循环体;
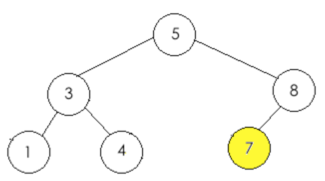
a、判断左接点是否为空,条件为真,于是乎直接生成左接点:node.left = TreeNode(7, 5)
所以此时的二叉树结果如下:
#######################################################################
Loop7: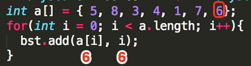
其第一个add(int value, int position)的参数为:value=6、position=6;
①、 ,判断root结点是否为null,条件为假,执行②;
,判断root结点是否为null,条件为假,执行②;
②、 ,调用第二个add(int value, int position, TreeNode node)方法:add(6, 6, root=TreeNode(5, 0));
,调用第二个add(int value, int position, TreeNode node)方法:add(6, 6, root=TreeNode(5, 0));
③、 ,其条件为假,继续执行④;
,其条件为假,继续执行④;
④、 ,其中要添加的元素在二叉树中木有重复,也就是得保证二叉树中不可能有相同的元素条件为假,继续⑤;
,其中要添加的元素在二叉树中木有重复,也就是得保证二叉树中不可能有相同的元素条件为假,继续⑤;
⑤、 ,判断要插入的值是否比指定的结点小,6 < 5 为假,继续执行⑥:
,判断要插入的值是否比指定的结点小,6 < 5 为假,继续执行⑥:
⑥、
a、判断右接点是否为空,条件为假,于是执行b;
b、add(6, 6, node.right=(8, 1));继续递归:
b③、 ,其条件为假,继续执行④;
,其条件为假,继续执行④;
b④、 ,其中要添加的元素在二叉树中木有重复,也就是得保证二叉树中不可能有相同的元素条件为假,继续⑤;
,其中要添加的元素在二叉树中木有重复,也就是得保证二叉树中不可能有相同的元素条件为假,继续⑤;
b⑤、 ,判断要插入的值是否比指定的结点小,6 < 8 为真,执行循环体;
,判断要插入的值是否比指定的结点小,6 < 8 为真,执行循环体;
a、判断左接点是否为空,条件为假,继续执行b;
b、add(6, 6, node.right=(7, 5));继续递归:
bb③、 ,其条件为假,继续执行④;
,其条件为假,继续执行④;
bb④、 ,其中要添加的元素在二叉树中木有重复,也就是得保证二叉树中不可能有相同的元素条件为假,继续⑤;
,其中要添加的元素在二叉树中木有重复,也就是得保证二叉树中不可能有相同的元素条件为假,继续⑤;
bb⑤、 ,判断要插入的值是否比指定的结点小,6 < 7 为真,执行循环体;
,判断要插入的值是否比指定的结点小,6 < 7 为真,执行循环体;
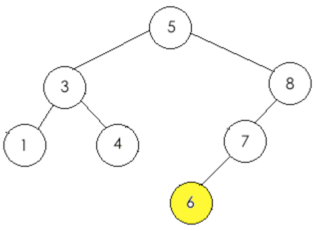
a、判断左接点是否为空,条件为真,于是乎直接生成左接点:node.left = TreeNode(6, 6)
所以此时的二叉树结果如下:
#######################################################################
于此二叉搜索树就已经完成了~~上面过程有点繁锁,重在体会!!!
第二步:从二叉树中进行数查找:
public class BinarySearchTree {
TreeNode root = null;
class TreeNode{
int value;
int position;
TreeNode left = null, right = null;
TreeNode(int value, int position){
this.value = value;
this.position = position;
}
}
public void add(int value, int position){
if(root == null){//生成一个根结点
root = new TreeNode(value, position);
} else {
//生成叶子结点
add(value, position, root);
}
}
private void add(int value, int position, TreeNode node){
if(node == null)
throw new RuntimeException("treenode cannot be null");
if(node.value == value)
return; //ignore the duplicated value
if(value < node.value){
if(node.left == null){
node.left = new TreeNode(value, position);
}else{
add(value, position, node.left);
}
}else{
if(node.right == null){
node.right = new TreeNode(value, position);
}else{
add(value, position, node.right);
}
}
}
//打印构建的二叉搜索树
static void printTreeNode(TreeNode node) {
if(node == null)
return;
System.out.println("node:" + node.value);
if(node.left != null) {
printTreeNode(node.left);
}
if(node.right != null) {
printTreeNode(node.right);
}
}
//搜索结点
public int search(int value){
return search(value, root);
}
private int search(int value, TreeNode node){
if(node == null)
return -1; //not found
else if(value < node.value){
System.out.println("Searching left");
return search(value, node.left);
}
else if(value > node.value){
System.out.println("Searching right");
return search(value, node.right);
}
else
return node.position;
}
public static void main(String[] args) {
BinarySearchTree bst = new BinarySearchTree();
int a[] = { 5, 8, 3, 4, 1, 7, 6};
for(int i = 0; i < a.length; i++){
bst.add(a[i], i);
}
// printTreeNode(bst.root);
System.out.println(bst.search(8));
System.out.println(bst.search(3));
System.out.println(bst.search(6));
System.out.println(bst.search(30));
}
}
编译运行:
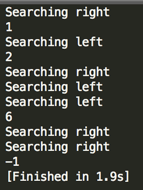
从上面运行结果中,拿搜6来说,只经过了三部:右、左、左,就从无序的数组中找到了,可见其效率是非常高的,最后会对其复杂度进行分析的,下面先来分析一下整个查找的过程:
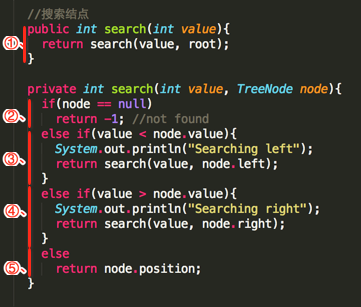
这里就以经过最多步找到“6”为例进行分析吧,
①、search(6, root=TreeNode(5, 0))
②、 ,其条件不满足,继续执行③;
,其条件不满足,继续执行③;
③、 ,6 < 5条件为假,执行④;
,6 < 5条件为假,执行④;
④、 ,6 > 5条件为真,执行条件体:
,6 > 5条件为真,执行条件体:
打印一下“Searching right”;然后search(6, node.right=TreeNode(8, 0))继续递归:
④②、 ,其条件不满足,继续执行③;
,其条件不满足,继续执行③;
④③、 ,6 < 8条件为真,执行条件体:
,6 < 8条件为真,执行条件体:
打印一下“Searching left”;然后search(6, node.left=TreeNode(7, 5))继续递归:
④③②、 ,其条件不满足,继续执行③;
,其条件不满足,继续执行③;
④③③、 ,6 < 7条件为真,执行条件体:
,6 < 7条件为真,执行条件体:
打印一下“Searching left”;然后search(6, node.left=TreeNode(6, 6))继续递归:
④③③②、 ,其条件不满足,继续执行③;
,其条件不满足,继续执行③;
④③③③、 ,6 < 6条件为假,继续执行④:
,6 < 6条件为假,继续执行④:
④、 ,6 > 6条件为假,继续执行⑤:
,6 > 6条件为假,继续执行⑤:
⑤、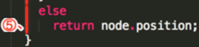 ,搜索到了结果直接返回,整个递归结束。
,搜索到了结果直接返回,整个递归结束。
时间复杂度分析:
如果写一个循环,从前匹配到尾,那时间复杂度是O(n),但是使用二叉树来搜索,它的复杂度肯定是小于n的,是跟树的深度有关的,每次递归一次树则向下走一层,那这个二叉搜索树的时间复杂度重点就是看一下树的深度是多少了,是多少呢?log ^ n ,所以说二叉搜索树查找的时间复杂度是O(log ^ n);
最新文章
- Leetcode Gray Code
- Infinite V2 Release Note
- Splinter学习--初探1,模拟百度搜索
- SpringAOP之静态代理
- bzoj1006 [HNOI2008]神奇的国度
- python之字符聊天小工具
- 完整导出IntelliJ IDEA的快捷键
- Neutron网络性能测试与分析(一) CVR
- linux_rsync定时备份
- Alex: 2018年对混合现实MR的展望
- 【一天一道LeetCode】#122. Best Time to Buy and Sell Stock II
- 第二节: 比较EF的Lambda查询和Linq查询写法的区别
- Android Demo Android ActionBarCompat-ListPopupMenu
- unity中Event Trigger组件应用代码
- Morley's Therorem(UVA11178+几何)
- 【BZOJ3879】SvT(后缀自动机,虚树)
- StiReport简单使用
- xml转json的方法
- 日志模块logging介绍
- 10 Examples of HotSpot JVM Options in Java[z]