Some Interesting Problems(持续更新中)
这种题目详解,是“一日一测”与“一句话题解”栏目所无法覆盖的,可能是考试用题,也可能是OJ题目。常常非常经典,可以见微知著。故选其精华,小列如下。
T1:fleet 给定一个序列,询问[L,R]间有多少种不同的权值。(普通数据结构范围)
e.g.:序列1,1,2,3,2的[1,5]有3种不同权值,[1,3]有2种不同权值。
ANSWER:可以考虑使用主席树求解。查询[L,R]时返回root[R]的[L,R]值之和。root[i]与root[i-1]的不同在于:prev[aa[i]]这个位置(即上一次出现aa[i]的位置)-1,在i这个位置+1。先预处理完毕,再应付查询。
T2:给定一个序列,询问[L,R]间有多少种权值k恰出现k次。(普通数据结构范围)
e.g.:序列1,1,2,3,2的[1,1]有1种权值,[1,2]有0种权值,[2,5]有2种权值。
ANSWER:可以考虑使用主席树求解。但是,我们也可以考虑使用离线。因为答案本质上统计的是一种情形,而我们可以考虑该情形对答案的贡献。如果把询问[L,R]转化为二维矩阵中某点[L,R]的权值,那么每一种情形的贡献也可以看做是矩形的修改。因为这样很令人不爽,可以进一步地转换,使用差分的思想,将矩形拆成4个角,问题于是转化为单点修改与矩阵前缀和的查询。这个东西很像BZOJ的一道题:MONICA。那是一道CDQ分治套树状数组的典型题目,因为有时间的先后。但是,这道题目完全可以先修改再查询,于是可以sort以后直接使用树状数组求解。然而,如果你真的能够看懂上面那段东西,你可能就会惊奇的发现,这种思路其实和主席树一模一样。于是,我们可以反观我们的学习过程。当我们在学主席树的时候,真的有想过离线的做法吗?
#define PN "count"
#include <cstdio>
#include <cstring>
#include <algorithm>
template<class T>inline void readint(T &res) {
static char ch;T flag=;
while((ch=getchar())<''||ch>'')if(ch=='-')flag=-;
res=ch-;
while((ch=getchar())>=''&&ch<='')res=res*+ch-;
res*=flag;
}
const int N = + ;
const int Q = + ;
struct DATUM {
int x, y, delta;
bool operator<(const DATUM &rhs) const {
if(x!=rhs.x) return x<rhs.x;
if(y!=rhs.y) return y<rhs.y;
if(delta!=rhs.delta) return delta<rhs.delta;
}
} data[N*+Q];
int tot, ans[Q];
inline void addD(int x,int y,int delta) {data[++tot]=(DATUM){x,y,delta};} int n, a[N];
void add(int pos,int val) {for(int x=pos;x<=n;x+=x&-x)a[x]+=val;}
int query(int pos) {int val=;for(int x=pos;x;x-=x&-x)val+=a[x];return val;} #include <vector>
std::vector<int> same[N];
int main() {
int q;readint(n);readint(q);
for( int i = ; i <= n; i++ ) same[i].push_back();
for( int i = , x, siz; i <= n; i++ ) {
readint(x);same[x].push_back(i);
siz=same[x].size();
if(siz>x) {
addD(same[x][siz-x-]+,i,+);
addD(same[x][siz-x]+,i,-);
if(siz>x+) addD(same[x][siz-x-]+,i,-);
if(siz>x+) addD(same[x][siz-x-]+,i,+);
}
}
for( int i = , l, r; i <= q; i++ ) readint(l),readint(r),addD(l,r,i+);
std::sort(data+,data+tot+);
for( int i = ; i <= tot; i++ ) {
if(data[i].delta<=) add(data[i].y,data[i].delta);
else if(data[i].y>=&&data[i].y<=n) ans[data[i].delta-]=query(data[i].y);
}
for( int i = ; i <= q; i++ ) printf("%d\n",ans[i]);
return ;
}
T3:给定n个长度为m的字符串,问有多少对字符串的相同字符数为0,为1,为2,为3,……为m。输出m+1个数。(总字符数≤1e5)
e.g.:4个长度为3的字符串xyz,xyz,zzx,xzz中有2对字符串的相同字符数为0,有1对字符串的相同字符数为1,有2对字符串的相同字符数为2,有1对字符串的相同字符数为3。
ANSWER:首先考虑暴力,是稳定的n^2*m,需要满足n约小于1000。然后,请忽略数据有意形成的数据断带。之后,对于m很小的情况,可以考虑暴力枚举出所有的字符串(就是状态压缩),因为相同字符数为m的情况可以直接预知,而又可以枚举每一位局部不同然后加以统计。于是考虑DP[2][S][j],表示在修改第i位时,与串S的相同字符数为j的串的数目。最后简单修改后,就可以输出答案。代码如下:
#define PN "words"
#include <cstdio>
#include <cstring>
#include <algorithm> const int N = + ;
int n, m;
long long bucket[N]; char s[N];
#define HOLE(x,y) s[(x-1)*m+y]
void bruce() {
for( int i = ; i <= n; i++ ) scanf("%s",s+(i-)*m);
for( int i = , j, k, tot; i <= n; i++ ) for( j = i + ; j <= n; j++ ) {
tot = ;
for( k = ; k < m; k++ ) if(HOLE(i,k)==HOLE(j,k)) tot++;
bucket[tot]++;
}
} const int APP = ;
const int M = ;
int appear[APP], cur, three[M];
long long f[][APP][M];
char ch;
void solve() {
for( int i = , now, j; i <= n; i++ ) {
now = ;
for( j = ; j <= m; j++, now*= ) {
while((ch=getchar())==' '||ch=='\n');ch-='x';
now+=ch;
}
appear[now/]++;
}
three[]=;
for( int i = ; i <= m; i++ ) three[i]=three[i-]*;
for( int i = ; i < three[m]; i++ ) f[cur][i][m]=appear[i];
for( int i = , j, k; i < m; i++ ) {
cur^=;memcpy(f[cur],f[cur^],sizeof(f[cur^]));
for( j = ; j < three[m]; j++ ) {
int s1 = (j/three[i]%)*three[i], s2 = j - s1;
for( k = ; k < three[i+]; k += three[i]) if(k!=s1) for( int p = m-i; p <= m; p++ ) f[cur][s2+k][p-]+=f[cur^][j][p];
}
}
for( int p = , i; p <= m; p++ ) for( i = ; i < three[m]; i++ ) bucket[p]+=appear[i]*f[cur][i][p];
bucket[m]-=n;
for( int i = ; i <= m; i++ ) bucket[i]/=;
} int main() {
freopen(PN".in","r",stdin);
freopen(PN".out","w",stdout);
scanf("%d%d",&n,&m);
if(m<=) solve();
else bruce();
for( int i = ; i <= m; i++ ) printf("%I64d\n",bucket[i]);
return ;
}
T4:BZOJ1001狼抓兔子。求无向方格图的最小割。
ANSWER:这样的最小割↔对偶图的最短路。dinic以前说过,但是对偶图确实可以快上很多倍(实验验证dinic约2500ms,对偶图约400ms)。因为这样的图的最小割一定是能够分隔源点与汇点的一段连续折线。于是可以把边之间的小“胞体”作为节点建边跑最短路。如图(摘自优秀博客http://www.cnblogs.com/jinkun113/p/4682827.html,同志们可以看一看):
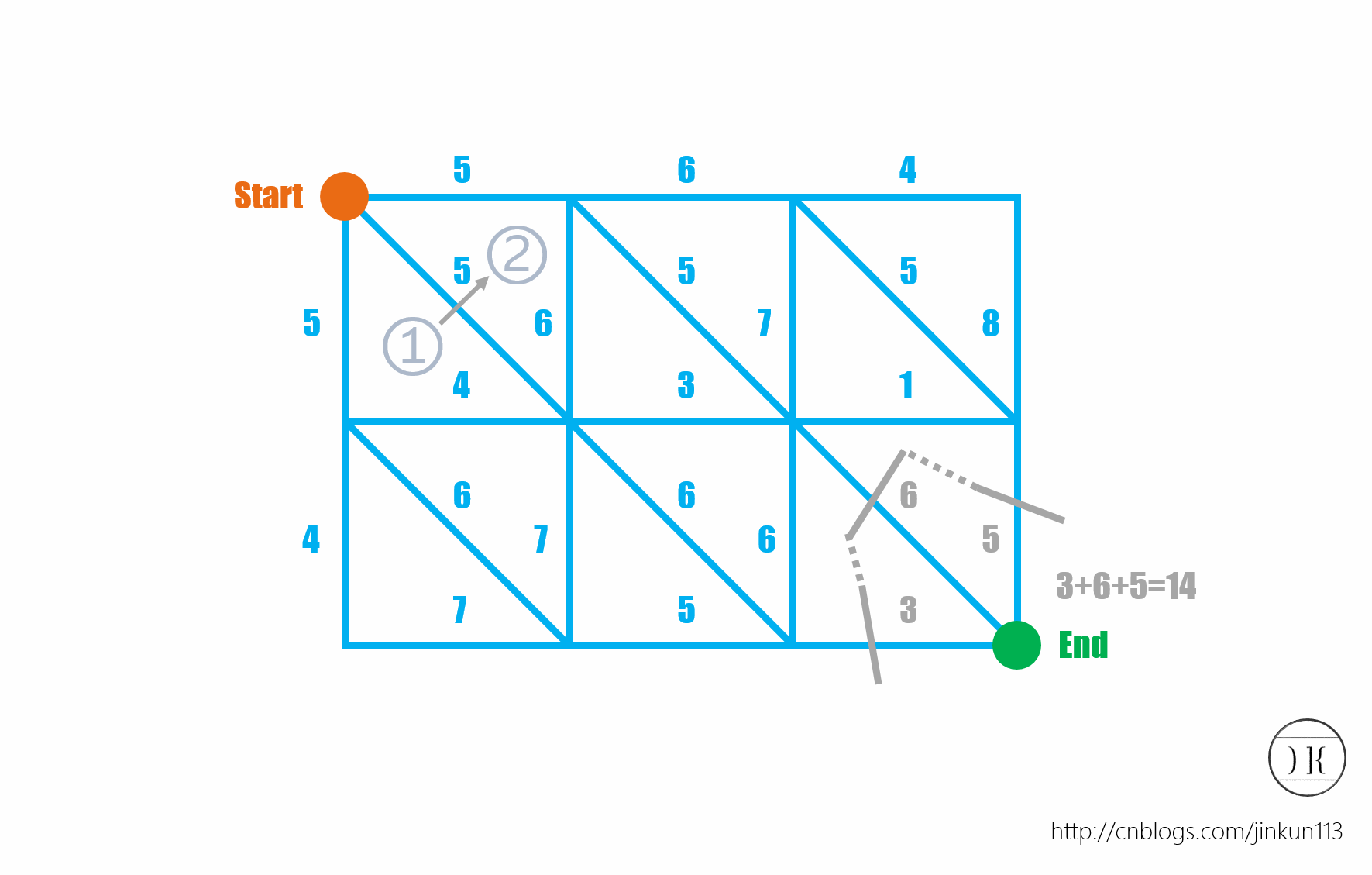

大概就是这样了。最后说一下,建议使用读入优化,不然结果会很让人伤心。
还有,对了,做完了可以看一看BZOJ2007[NOI2010]海拔,也是一道类似的题目,不过是有向边。
T5:随rand 给定n个正整数和一个模数mod。还有一个数x其初始值为1,我们将对x进行m次操作。每一次操作是从n个数中随机选出一个数p,然后x=x*p%mod。求x的期望值a/b,为避免输出浮点数请mod1e9+7后输出。(n≤1e5,m≤1e9,mod≤1e3)
e.g.:最开始有2个正整数1和2,mod=3,无论进行多少次操作,x总期望为3/2。
ANSWER:达哥出的题。这道题的暴力转移很好想。因为n和m看上去都很邪恶,而mod却很小,x再猖狂也是在0~mod-1这个范围内的。而最后答案的计算不过是a/b,a就是进行m次操作后每个模数的情况数乘以每个模数求和,而b就是进行m次操作后每个模数的情况数求和。中间“情况数”可以随便mod1e9+7。于是可以建立转移方程了。
方程:dp[i][j]=∑dp[i-1][k]*p[k][j]
在这里,dp[i][j]指进行i次操作后模数j的情况数mod1e9+7。p[k][j]指每一次操作,模数k能有几种转移到模数j的方法。我们可以发现,p[k][j]只与n个数本身有关,是妥妥的常量(特别是n没有用了)。加上滚动,这就是空间复杂度为O(mod^2)而时间复杂度为O(m*mod^2)的DP方法。
但是,m确实很大。考虑到DP方程确实太简单了,我们可以考虑使用矩阵快速幂。于是,空间复杂度仍为O(mod^2),而时间复杂度却成了O(log m*mod^3)。本题的前80%都有mod≤300,似乎80分稳了。在考场上我是这样认为的,但是我最后在老年机上只有20,在极速的floj上也只有50。只要仔细想一想,m最大为1e9,那log m就是30,mod^3=27000000,是绝对过不了的。不过,想到了这里,我们应该放弃吗?绝不!
我们知道O(log m*mod^3)是很慢的,但是O(log m*mod^2)却是可行的。考虑矩阵快速幂的本质,是对顺序的漠视。我们一节base算出来的,在本质上其实是进行若干次操作后1能够变成哪些模数。那么我们其实可以更加直接,因为可以直接乘起来。这样,时间复杂度打了标,空间复杂度亦变成了O(mod)。代码如下。
#define PN "rand"
#include <cstdio>
#include <algorithm>
#include <cstring> //char *hd, *tl, buf[(1<<15)+2];
//#define getc() ((hd==tl&&(tl=(hd=buf)+fread(buf,1,1<<15,stdin)),hd==tl)?0:*hd++)
template<class T>inline void readin(T &res) {
static char ch;T flag=;
while((ch=getchar())<''||ch>'')if(ch=='-')flag=-;
res=ch-;
while((ch=getchar())>=''&&ch<='')res=res*+ch-;
res*=flag;
} const int N = + ;
const int SIZ = + ;
const int MOD = 1e9+; #define set(x) (x>MOD?x-MOD:x)
int mod, base[SIZ], rus[SIZ], tmp[SIZ]; void calc() {
int a = , b = , ans;
for( int pos = ; pos < mod; pos++ ) a=set(a+(long long)rus[pos]*pos%MOD);
for( int pos = ; pos < mod; pos++ ) b=set(b+rus[pos]);
ans = a;
for( int bound = MOD - ; bound; bound>>=, b=(long long)b*b%MOD ) if(bound&) ans=(long long)ans*b%MOD;
printf("%d\n",ans);
} void matrix_(int type) {
for( int i = ; i < mod; i++ ) tmp[i]=;
if(!type) {
for( int i = , j; i < mod; i++ ) for( j = ; j < mod; j++ ) tmp[i*j%mod]=set(tmp[i*j%mod]+(long long)base[i]*base[j]%MOD);
for( int i = ; i < mod; i++ ) base[i]=tmp[i];
} else {
for( int i = , j; i < mod; i++ ) for( j = ; j < mod; j++ ) tmp[i*j%mod]=set(tmp[i*j%mod]+(long long)base[i]*rus[j]%MOD);
for( int i = ; i < mod; i++ ) rus[i]=tmp[i];
}
} int main() {
freopen(PN".in","r",stdin);
freopen(PN".out","w",stdout);
int n, m;readin(n);readin(m);readin(mod);
// memset(rus,0,sizeof(rus));memset(base,0,sizeof(base));
for( int i = , x, pos; i <= n; i++ ) {
readin(x);
for( pos = ; pos < mod; pos++ ) base[x]++;
}
rus[]=;
for( int bound = m; bound; bound>>=, matrix_() ) if(bound&) matrix_();
calc();
return ;
}
T6:BZOJ 2064 状压DP 给定一个初始集合和目标集合,有两种操作:1.合并集合中的两个元素,新元素为两个元素之和 2.分裂集合中的一个元素,得到的两个新元素之和等于原先的元素。要求用最小步数使初始集合变为目标集合,求最小步数。
ANSWER:当时特别迷,不知道怎么办。后来看了一下题解,实质上是最优子结构的应用。最优子结构操作起来很像套娃。因为最坏情况就是把所有的元素合并成一个,然后再拆开,步数为n+m-2。而我们可以发现,如果一个集合要变成另一个集合,而两个集合都分别存在一个子集之和相等,那么就可以减少2次操作,减少的是一次合并与一次拆分。然后,我们就可以枚举原始集合与目标集合,统计其中可以减少的次数。对于两个给定的集合,我们可以枚举其中的每一个元素,这样就可以间接查询所有子集了。如果两个集合之和相等,那么就可以减少一次操作。最后答案为n+m-2*f[(1<<n)-1][(1<<m)-1]。这是二维的。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define smax(x,y) x=std::max(x,y)
const int N = ;
int n, m, a[N+], b[N+], suma[<<N], sumb[<<N], f[<<N][<<N];
int main() {
scanf("%d",&n);
for( int i = ; i <= n; i++ ) scanf("%d",&a[i]);
scanf("%d",&m);
for( int i = ; i <= m; i++ ) scanf("%d",&b[i]);
for( int i = , pos = ; pos <= n; i<<=, pos++ ) suma[i]=a[pos];
for( int j = , pos = ; pos <= m; j<<=, pos++ ) sumb[j]=b[pos];
for( int i = , lima = <<n, k = i&-i; i < lima; i++, k = i&-i ) suma[i]=suma[k]+suma[i-k];
for( int j = , limb = <<m, k = j&-j; j < limb; j++, k = j&-j ) sumb[j]=sumb[k]+sumb[j-k];
for( int i = , j, k, lima = <<n, limb = <<m; i < lima; i++ ) for( j = ; j < limb; j++ ) {
for( k = ; k <= i; k<<= ) if(i&k) smax(f[i][j],f[i-k][j]);
for( k = ; k <= j; k<<= ) if(j&k) smax(f[i][j],f[i][j-k]);
if(suma[i]==sumb[j]) f[i][j]++;
}
printf("%d\n",n+m-*f[(<<n)-][(<<m)-]);
return ;
}
但是,考虑到原始集合与目标集合的实质差异并不大,只是在减少操作时在等号两边,于是可以考虑移项,原始集合是正的,而目标集合是负的,就可以统一考虑了。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define smax(x,y) x=std::max(x,y)
const int N = ;
int n, m, sum[<<N], f[<<N];
int main() {
scanf("%d",&n);
for( int i = , sta = ; i <= n; i++, sta<<= ) scanf("%d",&sum[sta]);
scanf("%d",&m);
for( int i = , x, sta = <<n; i <= m; i++, sta<<= ) {
scanf("%d",&x);
sum[sta]=-x;
}
n+=m;
for( int i = , lim = <<n, k = i&-i, p; i < lim; i++, k = i&-i ) {
sum[i]=sum[k]+sum[i-k];
for( p = ; p <= i; p<<= ) if(i&p) smax(f[i],f[i-p]);
if(sum[i]==) f[i]++;
}
printf("%d\n",n-*f[(<<n)-]);
return ;
}
T7:IRREGULAR 给你一棵树,每个点有点权,输出1~n每个点的困难度。一个点P的困难度是指,所有LCA为P的点对的路径异或和的最大值。点对可以是相同的2个点。按DFS序维护可持久化TRIE,为差量全局桶,询问时启发式合并。
E.G:对于一棵5个结点的树,1为根有儿子2、3和5,2和5是叶子结点,3有儿子4。5个点的权值分别为1775、6503、8147、2354和8484,可以算出这5个点的困难度分别为16044、6503、8147、2354和8484。
ANSWER:对于最大异或和这种经典问题,一个很直观的想法就是使用01TRIE。但是,本人当时一直是想使用DFS进行统计,将下面的所有直接合并到上面,显然不可行。于是考场上选择暴力枚举点对写ST表,无奈其他地方时间耗费太多,有东西没考虑到,这道题连暴力分也没有得到。
事后发现了一个性质(其实我以前曾经知道),就是u点到v点的路径异或和=dis[u]^dis[v]^dis[LCA]^aa[LCA],这里dis[u]指从u向上到根的点权异或和,aa[LCA]当然就是LCA的点权啦。
然后根据这个性质可以发现,其实不用从下往上,直接用可持久化TRIE树和DFS序就好了。于是可以先搞出DFS序,再构造出可持久化TRIE,再顺着统计每个结点的答案,因为一棵子树的DFS序是连续的,就可以很方便地统计询问了。
这样似乎是可以的,但是复杂度其实没有办法保证,于是考虑启发式合并。使用重链剖分方便地保证重子树优先,然后就小幷大了。
上面似乎说地很抽象,但最后实施起来其实是很具体的。但是中间有一点小细节还是让我调了很久。一处是query查询[L,R]时减的是L-1,还有一处是insert是siz的处理。
代码如下:
#define PN "irregular"
#include <cstdio>
#include <cstring>
#include <algorithm> template<class T>inline void readin(T &res) {
static char ch;T flag = ;
while((ch=getchar())<''||ch>'')if(ch=='-')flag=-;
res=ch-;
while((ch=getchar())>=''&&ch<='')res=res*+ch-;
res*=flag;
} const int N = + ;
const int ROOT = ;
struct Edge {int v,upre;}g[N<<];
int head[N], ne = ;
inline void adde(int u,int v) {g[++ne]=(Edge){v,head[u]};head[u]=ne;} int n, aa[N]; int fa[N], dis[N], s[N], son[N];
void DFS(int u) {
dis[u]=dis[fa[u]]^aa[u];
s[u]=;
for( int i = head[u], v; i; i = g[i].upre ) {
if((v=g[i].v)==fa[u]) continue;
fa[v]=u;
DFS(v);
s[u]+=s[v];
if(s[son[u]]<s[v]) son[u]=v;
}
} int in[N], out[N], seq[N], idy;
void DFS2(int u) {
in[u]=++idy;seq[idy]=u;
if(son[u]) DFS2(son[u]);
for( int i = head[u], v; i; i = g[i].upre ) {
if((v=g[i].v)==fa[u]||v==son[u]) continue;
DFS2(v);
}
out[u]=idy;
} const int BITS = ;
const int NODES = N * ;
int digit[BITS], root[N], siz[NODES], ch[NODES][], tail;
int query(int L,int R,int x) {
L = root[L], R = root[R];
for( int floor = ; floor < BITS; floor++,x>>= ) digit[floor]=x&;
int ans = ;
for( int floor = BITS - ; floor >= ; floor-- ) {
ans<<=;
if(siz[ch[R][digit[floor]^]]-siz[ch[L][digit[floor]^]]) {
ans++;
L = ch[L][digit[floor]^], R = ch[R][digit[floor]^];
} else L = ch[L][digit[floor]], R = ch[R][digit[floor]];
}
return ans;
} int main() {
freopen(PN".in","r",stdin);
freopen(PN".out","w",stdout);
readin(n);
for( int i = ; i <= n; i++ ) readin(aa[i]);
for( int i = +, u, v; i < n; i++ ) {
readin(u);readin(v);
adde(u,v);adde(v,u);
}
fa[ROOT]=ROOT;
DFS(ROOT);
DFS2(ROOT);
for( int i = ; i <= n; i++ ) {
for( int floor = , x = dis[seq[i]]; floor < BITS; floor++,x>>= ) digit[floor]=x&;
int ori = root[i-], now = root[i] = ++tail;
for( int floor = BITS - ; floor >= ; floor-- ) {
siz[now]=siz[ori]+;
ch[now][digit[floor]^]=ch[ori][digit[floor]^];
ori = ch[ori][digit[floor]];
now = ch[now][digit[floor]] = ++tail;
}
siz[now]=siz[ori]+;//注意此处
}
for( int u = ; u <= n; u++ ) {
int ans = aa[u];
if(son[u]) ans = std::max(ans,query(in[son[u]]-,out[son[u]],dis[u]^aa[u]));//注意左端减一
for( int v = seq[out[son[u]]+], x; fa[v]==u; v = seq[out[v]+] ) {
for( x = in[v]; x <= out[v]; x++ )
ans = std::max(ans,query(in[u]-,in[v]-,dis[seq[x]]^aa[u]));
}
printf("%d\n",ans);
}
return ;
}
IRREGULAR
T8:给一个n行m列的矩阵,你需要填入一些数。每一行有两个限制的li与ri(1≤li<ri≤m),要求每一行在1~li与ri~m之间都恰填入一个数,而每一行共填入2个数。每列最多填入1个数。问最后的方案数,%998244353。
E.G.:n=2,m=6,l1=2,r1=4,l2=5,r2=6。方案数共12。
ANSWER:DP,基于未来状态,造坑与填坑。因为每一列最多填入一个数,所以很容易知道行其实没有用。实质上是在填一些区间。于是就可以每一列不断右推,左端点必须不断填入,而右端点要么填入,要么留在未来。如此想来就很简单了。
bukl[i]表示L为i的情况数,bukr[i]表示R为i的情况数。dp[i][j]表示枚举到填入第i列,而已经枚举到的右区间有j个还将要被填的方案数。
dp[i][j+bukr[i]]<-dp[i-1][j]*P(i-j+S,bukl[i]) 之前已经填入了一些数,于是还剩i-j+S个确定的位置,然后把bukl[i]个数填入,bukr[i]个右端点的都放到未来
dp[i][j+bukr[i]-1]<-dp[i-1][j]*P(i-j+S-1,bukl[i])*(j+bukr[i]) 之前已经填入了一些数,又在此列填了一个右区间的数,于是还剩i-j+S-1个确定的位置,然后把bukl[i]个数填入
实在是很优啊!LKQ说这种DP太偏,其实不然。之前已经有不少题都是这样了,像BZOJ4321,像CF的超级二叉树……
T9:从前有一个旅馆,老板特别喜欢数字4和7。所以,他只让一个房间里住4或7个人。现在告诉你每个房间住的人数(7人以内),将一个原在i号房间的人移动到j房间的代价是abs(i-j),要想能满足老板的要求,花费的代价是多少?
ANSWER:发现人都是一样的。所以说,一个人从i号房间移动到j号房间其实可以理解为:(不妨设i<j)一个人从i号房间移动到i+1号房间,同时一个人从i+1号房间移动到i+2号房间,同时一个人从i+2号房间移动到i+3号房间,……,同时一个人从j-1号房间移动到j号房间。每一次这样的“一个人从i号房间移动到i+1号房间”代价为1,实质上是拆分了移动。设“从i号房间移动到i+1号房间的人数”=g[i](g[i]为负表示反向),则一个房间最后的人数=每个房间原来住的人数+g[i-1]-g[i]。根据题意,一个房间最后要么为0要么为4要么为7,于是g[i]只依赖于g[i-1]。考虑到一个房间至多7个人,所以说可以知道g[i]∈[-7,+7]否则不优,于是选7做临界点,开个15的数组就好了。方便处理边界,设置g[0]和g[n],可知他们都是0。
T10:【NOIP普及组车站分级】一条单向的铁路线上,依次有编号为 1, 2, …, n 的 n 个火车站。每个火车站都有一个级别,最低为 1 级。现有若干趟车次在这条线路上行驶,每一趟都满足如下要求:如果这趟车次停靠了火车站 x,则始发站、终点站之间所有级别大于等于火车站 x 的都必须停靠。(注意:起始站和终点站自然也算作事先已知需要停靠的站点)现有 m 趟车次的运行情况(全部满足要求) ,试推算这 n 个火车站至少分为几个不同的级别。请注意,n≤100000,m≤50000,∑si≤100000
ANSWER:原题的 n, m ≤ 1000,都要用上虚点(高级点连虚点,虚点连低级点)。像这道题,单单这种技巧便显得十分无力。考虑原题中虚点的作用,是把重复的东西捆在一起。如果你做过BZOJ萌萌哒,那你会觉得一切好像曾经都遇见过。当时做这道题目,我用了极其神奇的分块,就是这种想法。当然,那道题目用的实质上是倍增(因为倍增空间大一点但跑得飞快),这道题目也一样。倍增就是len+len->2len的方法,这么去做。但是我当时害怕炸空间,就再次深入思考,发现线段树也能够覆盖区间,而且结点数更少。直到最后才发现,使用线段树后结点会少很多但转移边少不到哪儿去,空间小时间相应更大。可是,提交之后两个方法最初都WA了,迷乱之中终于发现虚点也可以有边权。
代码如下(个人认为很清真):
#define PN "c"
#include <cstdio>
#include <cstring>
#include <algorithm> const int SIZ = + ;
const int M = + ;
struct EDGE {int v,upre;}g[M];
int head[SIZ], ne = ;
int in[SIZ], level[SIZ], pos[SIZ], idc;
bool mark[SIZ];
inline void adde(int u,int v) {in[v]++;g[++ne]=(EDGE){v,head[u]};head[u]=ne;} #include <queue>
std::queue<int> q;
int n;
void solve() {
int u, i, v, ans = ;
q.push();//破缺者
for( i = ; i <= n; i++ ) if(!in[pos[i]]) q.push(pos[i]), level[pos[i]]=;
while(!q.empty()) {
u = q.front();q.pop();
for( i = head[u], v; i; i = g[i].upre ) {
v = g[i].v;
in[v]--;if(!in[v]) q.push(v);
level[v]=std::max(level[v],level[u]+mark[v]);
ans=std::max(ans,level[v]);
}
}
printf("%d\n",ans);
} struct NODE {
int id;
NODE *ls, *rs;
} pool[SIZ], *tail=pool, *root;
NODE *build(int lf,int rg) {
NODE *nd=tail++;nd->id=++idc;
if(lf==rg) mark[nd->id]=, pos[lf]=nd->id;
else {
int mid=(lf+rg)>>;
nd->ls=build(lf,mid);
adde(nd->ls->id,nd->id);
nd->rs=build(mid+,rg);
adde(nd->rs->id,nd->id);
}
return nd;
}
void addedge(NODE *nd,int lf,int rg,int L,int R,int linkpoint) {
if(L<=lf&&rg<=R) {
adde(nd->id,linkpoint);
return ;
}
int mid=(lf+rg)>>;
if(L<=mid) addedge(nd->ls,lf,mid,L,R,linkpoint);
if(mid<R) addedge(nd->rs,mid+,rg,L,R,linkpoint);
} int main() {
freopen(PN".in","r",stdin);
freopen(PN".out","w",stdout);
int m;
scanf("%d%d",&n,&m);
root=build(,n);
for( int i = , j, s, last, now, linkpoint; i <= m; i++ ) {
scanf("%d%d",&s,&last);linkpoint=++idc;
adde(,linkpoint);//破缺者
adde(linkpoint,pos[last]);
for( j = ; j < s; j++ ) {
scanf("%d",&now);adde(linkpoint,pos[now]);
addedge(root,,n,last+,now-,linkpoint);
last = now;
}
}
solve();
return ;
}
线段树
#define PN "c"
#include <cstdio>
#include <cstring>
#include <algorithm> const int S = ;
const int SIZ = + ;
const int M = + ;
struct EDGE {int v,upre;}g[M];
int head[SIZ], ne = , in[SIZ], level[SIZ];
inline void adde(int u,int v) {in[v]++;g[++ne]=(EDGE){v,head[u]};head[u]=ne;} int n, base[S];
inline int HOLE(int dep,int pos) {return base[dep]+pos;} #include <queue>
std::queue<int> q;
void solve() {
int u, i, v, ans = ;
q.push();//破缺者
for( i = ; i <= n; i++ ) if(!in[i]) q.push(i), level[i]=;
while(!q.empty()) {
u = q.front();q.pop();
for( i = head[u], v; i; i = g[i].upre ) {
v = g[i].v;
in[v]--;if(!in[v]) q.push(v);
level[v]=std::max(level[v],level[u]+(v<=n));
ans=std::max(ans,level[v]);
}
}
printf("%d\n",ans);
} int main() {
freopen(PN".in","r",stdin);
freopen(PN".out","w",stdout);
int m, tot;
scanf("%d%d",&n,&m);tot=n;
for( int len = , dep = , pos; len < n; len <<= , dep++ ) {
base[dep]=tot;
for( pos = ; pos <= n - len + ; pos++ )
adde(HOLE(dep-,pos),HOLE(dep,pos)),adde(HOLE(dep-,pos+(len>>)),HOLE(dep,pos));
tot += n - len + ;
}
for( int i = , j, s, last, now, linkpoint, pos, dep, len, t; i <= m; i++ ) {
scanf("%d%d",&s,&last);linkpoint=++tot;
adde(,linkpoint);//破缺者
adde(linkpoint,last);
for( j = ; j < s; j++ ) {
scanf("%d",&now);adde(linkpoint,now);
for( pos = last+, dep = , len = , t = now - last - ; t; dep++, len<<=, t>>= ) if(t&)
adde(HOLE(dep,pos),linkpoint), pos+=len;
last = now;
}
}
solve();
return ;
}
倍增
T11:超立方体。点是0维元素(超立方体),线是1维元素(超立方体),面是2维元素(超立方体),体是3维元素(超立方体)。例如,4维超立方体由16个0维元素、32个1维元素、24个2维元素、8个3维元素和1个4维元素构成。现询问一个n维的超立方体分别由多少超立方体构成。(n≤1e7)
ANSWER:一个n维的超立方体与一个n维的直角坐标系息息相关。n维直角坐标系的实质是n个相互垂直的单位向量。单位向量就是2个点,也就是说每一维只有2种状态。考虑共点的情况,就是n维的状况完全一致。然后点分开,变成共线,就是n-1维的状况完全一致。之后共面,又有一维分开,n-2维的情况完全一致……于是发现,共“i”维,就是n-i维的状况完全一致,而其他i维可以自由选取,每一种共“i”维的情况就定出了一个i维超立方体。所以i维超立方体共有C(n,n-i)*2n-i个。
怎么求C排列数?大概有以下几种情况:

法一是暴力杨辉三角(时空复杂度过大,预处理O(n^2))。
法二是预处理阶乘逆元(要求模数有逆元,预处理复杂度O(n))。
法三是lucas定理(要求模数是质数且不能过大,单次O(p*logpn))。
法四是线性筛因数(模数任意,预处理复杂度O(n),查询O(lgn))。
但这里其实是法五。因为C(n,i)=C(n,i-1)*(n-i+1)/i,而且模数是质数,复杂度O(n)。当然,这种算法基本上没有任何用处。
但我还是提一下
T12:BZOJ 4726 SABOTA 某个公司有n个人, 上下级关系构成了一个有根树。其中有个人是叛徒(这个人不知道是谁)。对于一个人, 如果他下属(直接或者间接, 不包括他自己)中叛徒占的比例超过x,那么这个人也会变成叛徒,并且他的所有下属都会变成叛徒。你要求出一个最小的x,使得最坏情况下,叛徒的个数不会超过k。
ANSWER:叛徒?不是公司,是黑帮吧……如果x小了,叛徒就会有很多,就会超过k。如果x太大,也会是很不优的。一个直观的想法就是预处理siz后直接二分答案。WXH说不能二分,因为ta直接TLE了。于是,此题能够不DFS那就应该for。
怎么check呢?有几个很显然的事实:叶子变成叛徒的情况最坏,而整个过程是向上的感染,最后一定是一整个子树。知道了这件基本事实以后,我们就可以搞了。
#include <cstdio>
#include <cstring>
#include <algorithm> const int N = + ;
const double eps = 1e-;
int n, k, fa[N], siz[N];
double delta[N];
bool hack[N]; bool check(double mid) {
memset(hack,,sizeof(bool)*(n+));
for( int u = n; u >= ; u-- ) {
if(siz[u]==) hack[u]=;
if(hack[u]) {
if(siz[u]>k) return false;
if(delta[u]>mid+eps) hack[fa[u]]=;
}
}
return true;
} int main() {
scanf("%d%d",&n,&k);
for( int i = ; i <= n; i++ ) scanf("%d",&fa[i]);
for( int u = n; u >= ; u-- ) siz[u]++, siz[fa[u]]+=siz[u];
for( int u = n; u >= ; u-- ) delta[u] = siz[u]*1.0/(siz[fa[u]]-);
double lf = 0.0, rg = 1.0, mid, ans;
while(lf+eps<rg) {
mid = (lf+rg)/;
if(check(mid)) ans = mid, rg = mid;
else lf = mid;
}
printf("%lf\n",ans);
return ;
}
二分
但是这道题网上的人都说是树形DP。又是怎么回事?原来DP是一维的,表示该树不能被完全感染的最小的x。同样也是向上感染,状态也很好转移。如果子树u的大小大于k,那么ans就需要更新了,如果ans<dp[u],那么叛徒的个数就会超过k。
#include <cstdio>
#include <cstring>
#include <algorithm> const int N = + ;
int n, k, fa[N], siz[N];
double dp[N], ans;
inline void smax(double &a,double b) {a=std::max(a,b);} int main() {
scanf("%d%d",&n,&k);
for( int i = ; i <= n; i++ ) scanf("%d",&fa[i]);
for( int u = n; u >= ; u-- ) siz[u]++, siz[fa[u]]+=siz[u];
for( int u = n; u >= ; u-- ) {
if(siz[u]==) dp[u]=1.0;
if(siz[u]>k) ans=std::max(ans,dp[u]);
smax(dp[fa[u]],std::min(dp[u],siz[u]*1.0/(siz[fa[u]]-)));
}
printf("%lf\n",ans);
return ;
}
树形DP
互相比较,发现其实思想是差不多的。万变不离其宗嘛。
T13:KAND。现在给你n个数,从中选出k个数,询问有多少种方案使得这k个数的按位与等于r。模大质数输出。
ANSWER:看似无从下手。但是,确实存在一个很显然却很难想到的性质:当且仅当是几个包含s的数的按位与才能包含s。这里的包含,是把二进制的每一位当做元素,把每个数当做集合来看的。也就是说,只要我们知道了包含s的数的个数,就能很方便地算出n个数中选k个数按位与能够包含s的方案数。既然已经算到这里,就直接用一个小容斥就可以了。
再说一遍,我们选k个数按位与为r直接统计出结果很难,但是已经说过了,选k个数按位包含r的方案数很好统计,只需要统计出有多少个数包含r就好了,再组合一下容斥一下就能得出结果。但是,怎么统计出有多少个数包含r?如果使用纯暴力,最坏能够达到3n的复杂度。于是IFT横空出世。
IFT是一种计数系统,分阶段拆位转移,可以刚好统计出包含s的所有数。本质是把包含s的ss转移到s,有且只有一种方式转移。而其他的一定不能够得到转移,总的复杂度做到了k*2k。
(注:本人很久之后才发现,原来“IFT”就是FWT,普通的FWT是对半分,但是直接按位枚举是完全正确的,而且很优。)
代码如下:
#define PN "kand"
#include <cstdio>
const int N = 1e5+;
const int P = ;
const int MOD = 1e9+;
int n, k, s, lim, cnt[<<P], fac[N], vfac[N];
int mpow(int a,int b) {
int ans=;
for(;b;a=(long long)a*a%MOD,b>>=) if(b&) ans=(long long)ans*a%MOD;
return ans;
}
void init_comb() {
fac[]=;for( int i = ; i <= n; i++ ) fac[i]=(long long)fac[i-]*i%MOD;
vfac[n]=mpow(fac[n],MOD-);for( int i = n-; i>=; i-- ) vfac[i]=(long long)vfac[i+]*(i+)%MOD;
}
int comb(int n,int m) {
if(m>n) return ;
return (long long)fac[n]*vfac[m]%MOD*vfac[n-m]%MOD;
}
void fix(int &a) {if(a>=MOD)a-=MOD;if(a<)a+=MOD;}
void sum(int delta) {
for( int i = ; i < P; i++ ) {
int bit=<<i, s=lim--bit;
for( int ss=s; ss; ss=(ss-)&s ) {
cnt[ss]+=delta*cnt[ss|bit];
fix(cnt[ss]);
}
cnt[]+=delta*cnt[bit];
fix(cnt[]);
}
}
int main() {
freopen(PN".in","r",stdin);
freopen(PN".out","w",stdout);
scanf("%d%d%d",&n,&k,&s);lim=<<P;
for( int i = , x; i <= n; i++ ) scanf("%d",&x), cnt[x]++;
sum(+);
init_comb();for( int ss = ; ss < lim; ss++ ) cnt[ss]=comb(cnt[ss],k);
sum(-);
printf("%d\n",cnt[s]);
return ;
}
kand
未完待续……
最新文章
- Web.xml中设置Servlet和Filter时的url-pattern匹配规则
- C# 如何捕获键盘按钮和组合键以及KeyPress/KeyDown事件之间的区别 (附KeyChar/KeyCode值)
- 我的防Q+
- 2016030208 - sql50题练习题
- cocos2dx使用tolua关于字符串处理的一个问题
- Android 动态监听网络 断网重连
- Servlet支持上传多张图片
- Javascript数组(1)--基本属性及方法
- python3 excel文件的读与写
- hibernate(*.hbm.xml)中新添加的字段被标记为红色(找不到)的解决方法
- CF920E Connected Components?
- Flask三种导入配置文件的方式
- Beanstalkd消息队列的安装与使用
- es6学习笔记7--Set
- 浅谈 java 反射机制
- 服务治理-> Spring Cloud Eureka
- (转)生活中的OO智慧——大话面向对象五大原则
- Servlet:从入门到实战学习(2)---Servlet生命周期
- centos7 默认进入系统命令行模式修改
- 超酷的JavaScript叙事性时间轴(Timeline)类库