洛谷P6075题解

题面

首先这 \(n\) 个数是互相独立的，所以我们不需要统一的去考虑，只需要考虑其中一个数即可。

我们以 \(k=5\) 的情况举例。

我设 \(f_i\) 为最后一行只填前 \(i\) 个点的情况数， \(g_i\) 为 \(k=i\) 时总共的情况数。

显然， \(f_0\) 就是 \(g_{k-1}\) ，在这里就是 \(g_4\) 。

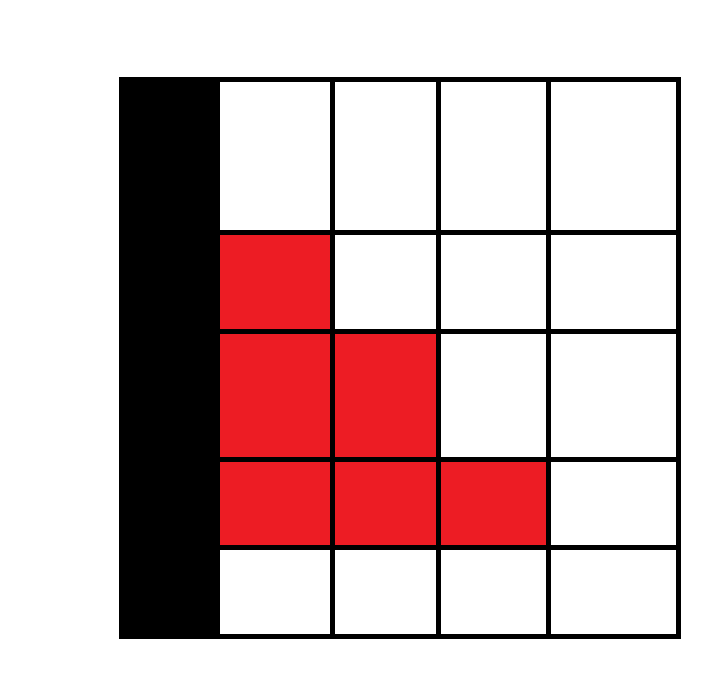
然后 \(f_1\) 其实就是图中黑色部分一定填，白色一定不填，红色部分可选的种类数。进一步观察，这个红色部分其实就是 \(g_3\) 。

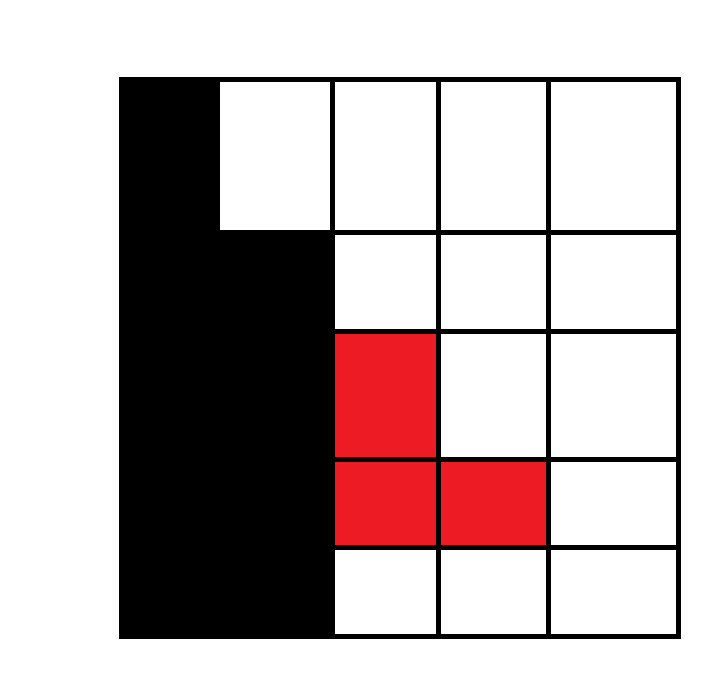
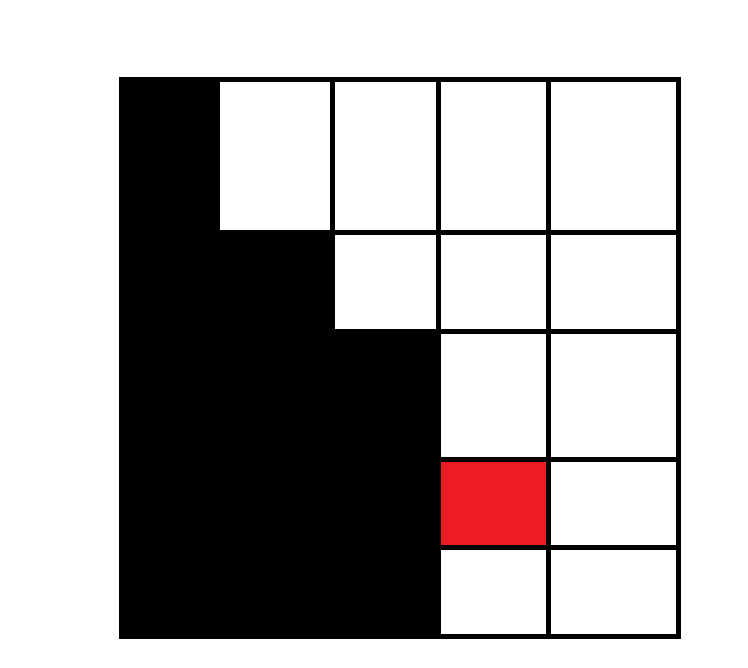
再进一步由图可以得到， \(f_2=g_2,f_3=g_1\) 。

再往下， \(f_4\) 和 \(f_5\) 都没得选了，所以 \(f_4=f_5=1\) 。

为了下面讲述方便，我们设 \(f_4=g_0=1\) 。

那么我们已经得到了 \(g_5=\sum^5_{i=1}f_i\) ，那么我们可以推广到其他数，可知 \(g_k=\sum^k_{i=1}f_i\)

再进一步观察，当 \(k=5\) 时， \(f_0=g_4,f_1=g_3,f_2=g_2,f_3=g_1,f_4=g_0\) ，

所以 \(g_5=\sum^5_{i=1}f_i=\sum^4_{i=1}g_{4-i}+f_5=\sum^4_{i=1}g_i+1\) 。

推广到其他数，可知 \(g_k=\sum^{k-1}_{i=1}g_i+1\)

那么我们可以根据 \(g_0=1\) 推出 \(g_1=2,g_2=4,g_3=8\) 。

观察规律，可以发现 \(g_i=2^i\) 。

如何证明呢？我们使用数学归纳法。

首先当 \(i=0\) 时，\(g_0=1=2^0\) ，结论成立。

再假设 \(i=k\) 时，结论已成立，那么 \(g_{k+1}=\sum^{k}_{i=1}g_i+1=\sum^{k-1}_{i=1}g_i+1+g_k\) ，而 \(\sum^{k-1}_{i=1}g_i+1=g_k\) ，所以 \(g_{k+1}=\sum^{k-1}_{i=1}g_i+1+g_k=2\times g_k=2\times 2^k=2^{k+1}\) ，所以 \(i=k+1\) 时仍然成立。

所以我们就证明出了 \(g_i=2^i\) 。

回到最开始。我们有 \(n\) 个数，每个数有 \(g_k=2^k\) 种选择，那么根据乘法原理，总计的选择数就是 \(2^{nk}\) 。用快速幂算一下即可。代码就不贴了。

巴特西

洛谷P6075题解

最新文章

热门文章