$\sum_{i = 1}^{n} k \bmod i = n * k - \sum_{i = 1}^{n} \lfloor k / i \rfloor * i$

显然，$\lfloor k / i \rfloor$ 是最棘手的，我们要想办法简化计算。

证明单调性

观察 $\lfloor k / i \rfloor$，显然随着 $i$ 的增大，这个式子是越来越小的。
又因为有向下取整符号，所以该式子取值只能是整数。

若我们设函数 $f(x) = \lfloor k / x \rfloor$。则画在坐标轴中应该是从高到低一条条横线。

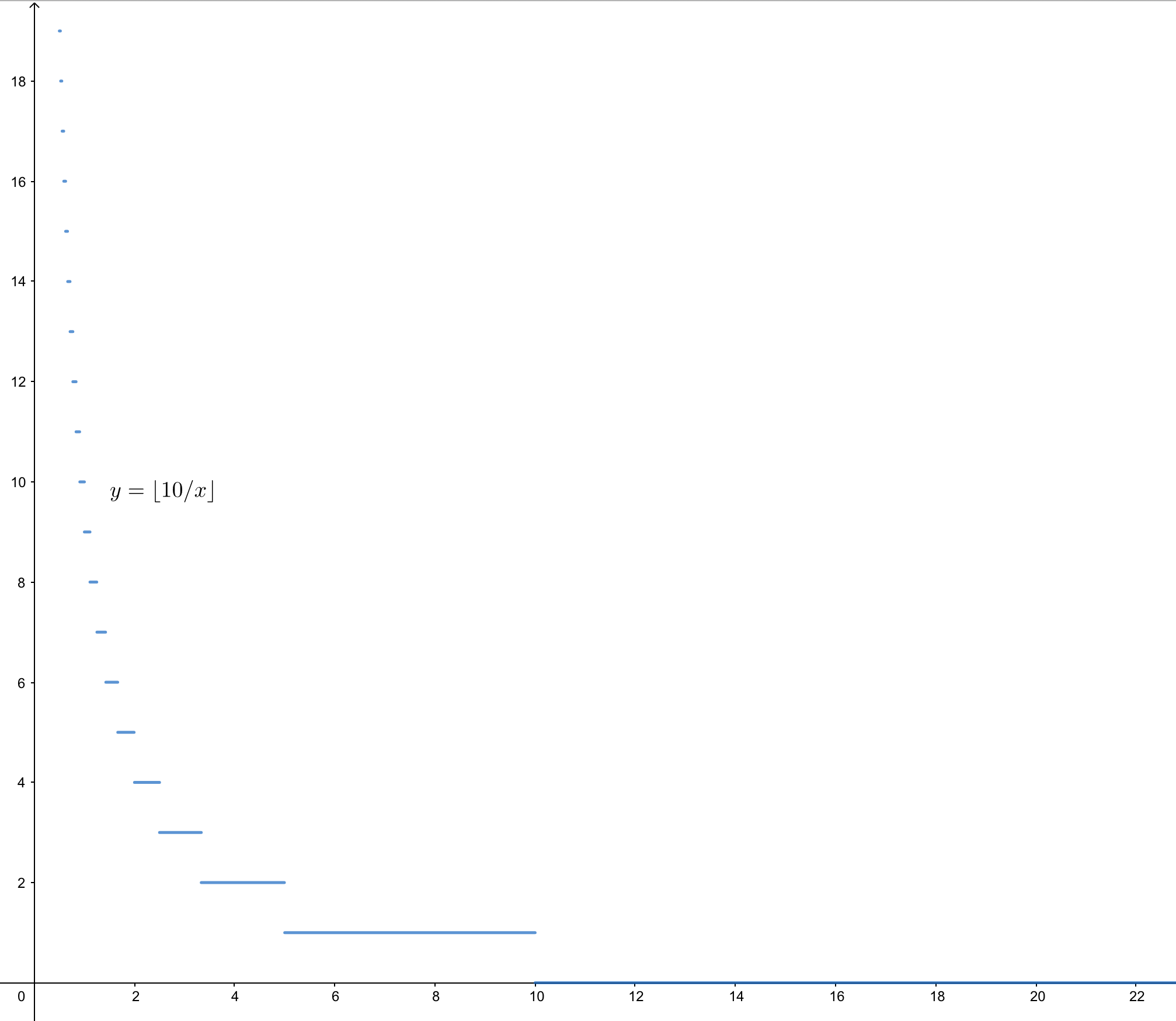
上图是一条 $f(x) = \lfloor 10 / x \rfloor$ 的图像。

证明该式子最多只有 $2\sqrt{k}$ 个取值

分段讨论：

当 $i <= \sqrt{k}$ 时，因为 $i$ 是 $1$ 到 $\sqrt{k}$ 的整数，所以最多只有 $\sqrt{k}$ 个不同的 $\lfloor k / i \rfloor$ 值。
当 $i > \sqrt{k}$ 时，$\lfloor k / i \rfloor <= \sqrt{k}$，又因为式子取整了，所以式子只能取$1$ 到 $\sqrt{k}$ 的整数，故最多也只有 $\sqrt{k}$ 个不同的 $\lfloor k / i \rfloor$ 值。

综上所述，$\lfloor k / i \rfloor$ 最多只有 $2\sqrt{k}$ 个取值

有关当 $i > \sqrt{k}$ 时，$\lfloor k / i \rfloor <= \sqrt{k}$ 的证明：

由于下取整，所以 $\lfloor k / i \rfloor * i <= k$ ①

假设 $\lfloor k / i \rfloor > \sqrt{k} $，有 $\lfloor k / i \rfloor * i > \lfloor k / i \rfloor * \sqrt{k} > \sqrt{k} ^ 2 = k$。②

① 与 ② 矛盾

通过以上步骤，我们可以知道这个答案由连续 $2\sqrt{k}$ 段不同的取值组成，那么我们只需要确定每种取值是下界 $l$ 和上界 $r$。通过 $\sum_{i = l}^{r} \lfloor k / i \rfloor * i = \sum_{i = l}^{r} \lfloor k / l \rfloor * i = \lfloor k / l \rfloor * (\sum_{i = l}^{r}i)$ 即可求得每一段对答案的贡献。$(\sum_{i = l}^{r}i)$ 可以用等差数列求和公式计算。

已知下界求上界

假设我们知道一段相同取值的下界是 $x$，若能求出上界，我们问题便解决了。

猜想若下界是 $x$，上界是 $r = \lfloor k / \lfloor k / x \rfloor \rfloor$

第一步、求证 $\lfloor k / x \rfloor = \lfloor k / r \rfloor$

由定义式可知 $r * \lfloor k / x \rfloor + q = k$ ③，其中 $0 <= q < \lfloor k / x \rfloor$，所以 $\lfloor k / r \rfloor = \lfloor\frac{r * \lfloor k / x \rfloor + q}{r}\rfloor = \lfloor k / x \rfloor + \lfloor \frac{q}{r} \rfloor >= \lfloor k / x \rfloor$
$r >= \lfloor k / (k / x ) \rfloor = x$，所以 $\lfloor k / x \rfloor >= \lfloor k / r \rfloor$

综上 $\lfloor k / x \rfloor = \lfloor k / r \rfloor$。

第二步、求证 $\lfloor k / (r + 1) \rfloor \not = \lfloor k / x \rfloor$

假设 $\lfloor k / (r + 1) \rfloor = \lfloor k / x \rfloor$

那么有 $(r + 1) * \lfloor k / x \rfloor + q' = k$，其中 $0 <= q < r + 1$

把式子变化一下：

$r * \lfloor k / x \rfloor + \lfloor k / x \rfloor + q' = k $ ④

③④ 联立，有：

$\lfloor k / x \rfloor + q' < \lfloor k / x \rfloor$

因为 $q' >= 0$，所以该式子矛盾，故假设不成立。

通过这两步及之前的单调性，我们知道 $\lfloor k / \lfloor k / x \rfloor \rfloor$ 一定是上界

算法

所以算法就很好设计了：

设 $l = 1$，算出上界 $r$。计算这段的贡献
使 $l = r + 1$，即跳到下一段计算贡献。
重复知道算完 $[1, n]$ 里所有段。

$Tips:$

当 $\lfloor k / l \rfloor = 0$ 的时候，显然这段以及后面（有单调性）已经没有贡献了，可以 $break$。（或者直接设右端点为 $n$）
注意右端点和 $n$ 取个 $min$，因为 $ > n$ 没有贡献了。

#include <cstdio>

#include <iostream>

using namespace std;

typedef long long LL;

int n, k, l, r;

LL ans;

int main() {

	scanf("%d%d", &n, &k);

	ans = (LL)n * k;

	for (l = 1; l <= n; l = r + 1) {

	    if(k / l == 0) break;

		r = min(k / (k / l), n);

		ans -= (LL)(k / l) * (l + r) * (r - l + 1) / 2;

	}

	printf("%lld\n", ans);

	return 0;

}

巴特西

AcWing 199. 余数之和

证明单调性

证明该式子最多只有 \(2\sqrt{k}\) 个取值

已知下界求上界

算法

最新文章

热门文章