分布，在计算机学科里一般是指概率分布，是概率论的基本概念之一。分布反映的是随机或某个系统中的某个变量，它的取值的范围和规律。

常见的分布有：二项分布、泊松分布、正态分布、指数分布等，下面对它们进行一一介绍。

PS：本文中谈到的PDF、PMF、CDF均为公认的缩写方式：

PDF：概率密度函数（probability density function）；

PMF：概率质量函数（probability mass function）；

CDF：累积分布函数（cumulative distribution function）。

二项分布

说起二项分布，离不开伯努利实验，二项分布就是重复N次的伯努利实验（伯努利实验，是指一种只有两种相反结果的随机试验，比如抛硬币，结果只有正面和反面；又比如投篮，只有投中和没有投中两种结果）。它的PMF可写作：

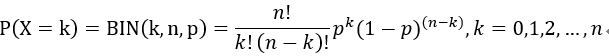
其中k为在n次实验中命中的次数，成功的概率为p。

二项分布的CDF可以写作：

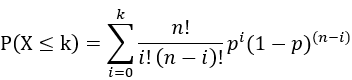
例子：抛10次硬币，有2次正面朝上的概率是多少？下面分别用C++实现和用numpy证明结果

C++实现：

#include <vector>

#include <iostream>

#include <iomanip>

double calc_binomial(int n, int k, double p)

{

  if(n < 0 || k < 0)

    return 0.0;

  std::vector< std::vector< double > > binomials((n + 1), std::vector< double >(k + 1));

  binomials[0][0] = 1.0;

  for(int i = 1; i < (n + 1); ++i)

    binomials[i][0] = (1.0 - p) * binomials[i - 1][0];

  for(int j = 1; j < (k + 1); ++j)

    binomials[0][j] = 0.0;

  for(int i = 1; i < (n + 1); ++i)

    for (int j = 1; j < (k + 1); ++j)

      binomials[i][j] = (1.0 - p) * binomials[i - 1][j] + p * binomials[i - 1][j - 1];

  return binomials[n][k];

}

int main()

{

  std::cout << std::fixed << std::setprecision(8) << calc_binomial(10, 2, 0.50) << std::endl;

}

结果为：0.04394531

Python实现：

import numpy as np

from scipy import stats

import matplotlib.pyplot as plt

def calc_binomial():

    n = 10

    p = 0.5

    k = 2

    binomial = stats.binom.pmf(k,n,p)

    print binomial

calc_binomial()

结果为：0.0439453125

反之，知道投10次硬币朝上的平均概率为0.3（即平均有3次朝上），试着从10000次实验中找出规律。

用C++实现：

#include <iostream>

#include <cmath>

#include <iomanip>

#include <vector>

#include <cstdlib>

#include <ctime>

int gen_binomial_rand(int n, double p)

{

  int k = 0;

  for(int i = 0; i < n; i++)

  {

    double current_probability = ((double)rand() / (double)RAND_MAX);

    if(current_probability < p)

    {

      k++;

    }

  }

  return k;

}

int main()

{

  srand((unsigned)time(NULL));

  int gn = 10;

  double gp = 0.3;

  int times = 10000;

  int sum_of_times = 0;

  std::vector< int > result(gn);

  for(int t = 0; t < times; t++)

  {

    int single_result = gen_binomial_rand(gn, gp);

    if(single_result < gn)

    {

      result[single_result]++;

    }

  }

  std::cout << std::endl;

  for(int i = 0; i < gn; i++)

  {

    sum_of_times += result[i];

    std::cout << result[i] << ",";

  }

  std::cout << std::endl;

  std::cout << "Total: " << sum_of_times << std::endl;

  return 0;

}

结果为：

323,1199,2310,2631,1951,1103,367,97,18,1,
Total: 10000

拿到Python里面用图表看一下：

import numpy as np

from scipy import stats

import matplotlib.pyplot as plt

def show_binom_rvs():

    n = np.array([323,1199,2310,2631,1951,1103,367,97,18,1])

    plt.plot(n)

    plt.show()

show_binom_rvs()

显示为：

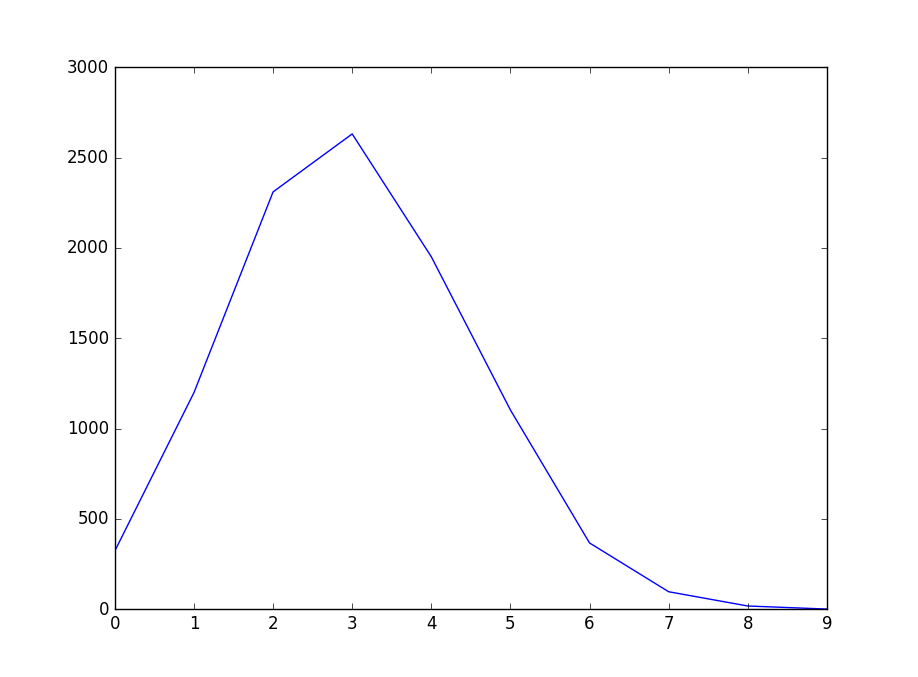
我们再来用Python的numpy和scipy的库来验证一下：

import numpy as np

from scipy import stats

import matplotlib.pyplot as plt

def calc_binom_rvs():

    binom_rvs = stats.binom.rvs(n=10,p=0.3,size=10000)

    plt.hist(binom_rvs, bins=10)

    plt.show()

calc_binom_rvs()

得到结果图片：

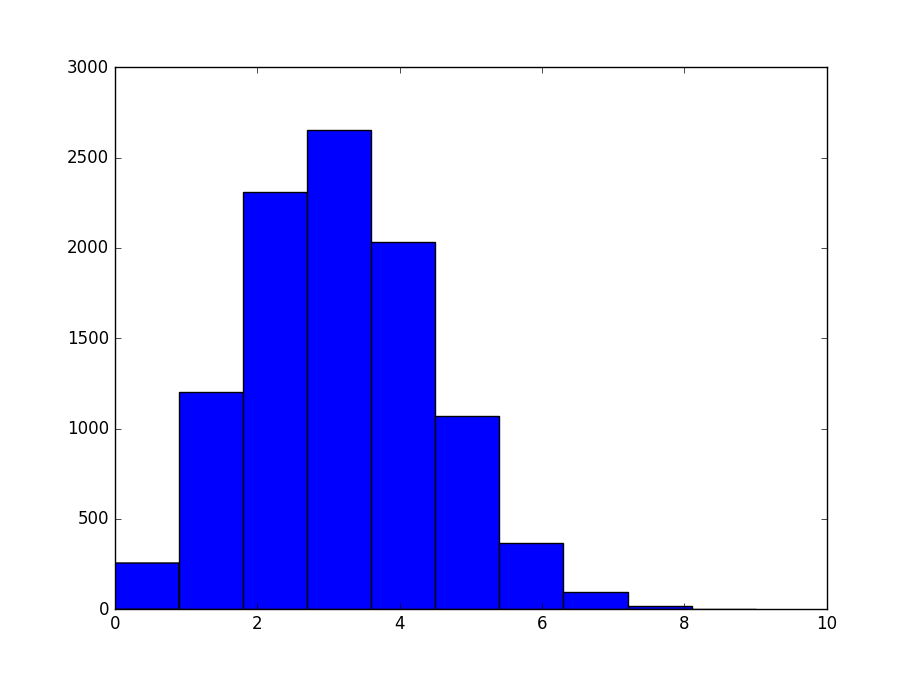
可以看到两次的图形包络是近似的。

泊松分布

在日常生活中，我们经常会遇到一些事情，这些事情发生的频率比较固定，但是发生的时间是不固定的，泊松分布就是用来描述单位时间内随机事件的发生概率。比如：知道一个医院平均每小时有3个小孩出生，那么下一个小时出生2个小孩的概率是多少？

泊松分布的PMF可以写作：

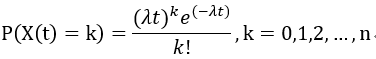
其中，t为连续时间长度，k为事件发生的次数，λ为发生事件的数学期望（如单位时间内发生事件的均值），e为自然底数。

就上面的例子，知道一个医院平均每小时有3个小孩出生，那么下一个小时出生2个小孩的概率是多少？用C++实现：

#include <iostream>

#include <cmath>

#include <iomanip>

double calc_poisson(int k, int lambda)

{

  double result;

  result = pow(lambda, k) * exp(-lambda);

  int factorial = 1;

  for(int i = 1; i <= k; i++)

  {

    factorial *= i;

  }

  result = result / factorial;

  return result;

}

int main()

{

  std::cout << std::fixed << std::setprecision(8) << calc_poisson(2, 3) << std::endl;

}

结果是：0.22404181

用Python验证：

import numpy as np

from scipy import stats

import matplotlib.pyplot as plt

def calc_poisson():

    lambd = 3

    k = 2

    y = stats.poisson.pmf(k,lambd)

    print y

calc_poisson()

结果是：0.224041807655

下面再用C++实现生成泊松随机数，并用Python检验：

C++实现：

#include <iostream>
#include <cmath>
#include <iomanip>
#include <vector>
#include <cstdlib>
#include <ctime>

double binary_random()
{
  double rand_number = (rand() % 100);
  rand_number /= 100;
  return rand_number;
}

int calc_poisson(int lambda)
{
  int k = 0;
  double p = 1.0;
  double l = exp(-lambda);

while(p >= l)
  {
    double r = binary_random();
    p *= r;
    k++;
  }
 
  return (k - 1);
}

int main()
{
  int t = 10000;
  int lambda = 3;
  int distribution = 20;
  int dist_cells[distribution] = {0};

srand((unsigned)time(NULL));

for(int i = 0; i < t; i++)
  {
    int n = calc_poisson(lambda);
    dist_cells[n]++;
  }

for(int i = 0; i < distribution; i++)
  {
    std::cout << dist_cells[i] << ",";
  }
  std::cout << std::endl;
 
 
  return 0;
}

运行结果为：467,1604,2298,2264,1608,952,466,217,87,29,6,2,0,0,0,0,0,0,0,0,

放入Python显示并和Python生成的比较：

import numpy as np

from scipy import stats

import matplotlib.pyplot as plt

def gen_poisson_rvs():

    dist = 20

    cpp_result = np.array([467,1604,2298,2264,1608,952,466,217,87,29,6,2,0,0,0,0,0,0,0,0])

    py_result = np.random.poisson(lam=3,size=10000)

    plt.hist(py_result,bins=dist,range=[0,dist],color='g')

    plt.plot(cpp_result,color='r')

    plt.show()

gen_poisson_rvs()

运行并显示图表为：

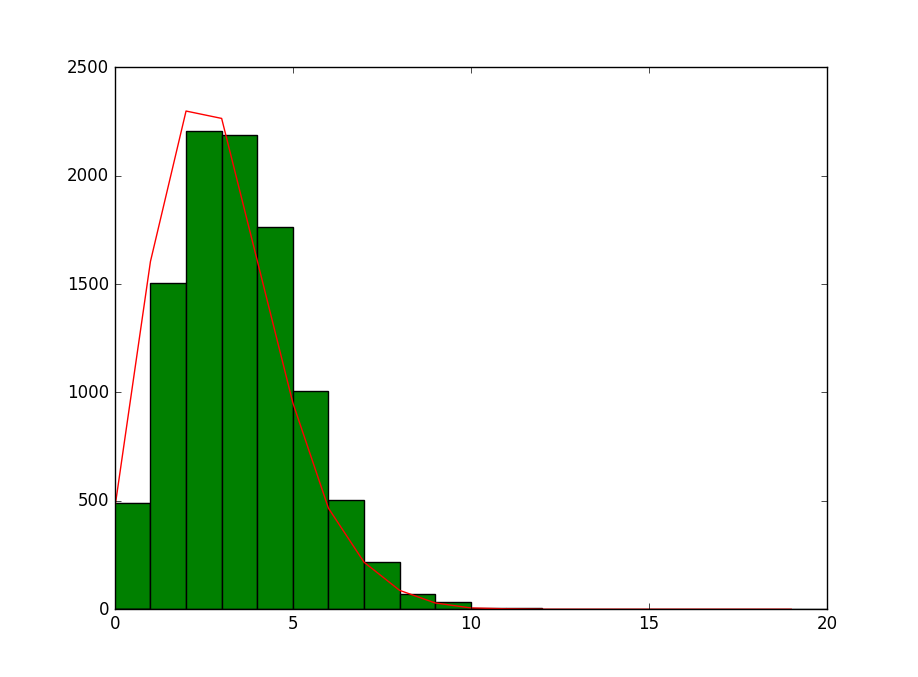
指数分布

指数分布，描述的是在某一事件发生后，在连续时间间隔内继续发生的概率。比如上面的例子，知道一个医院平均每小时有3个小孩出生，刚刚已经有一个小孩出生了，那么下一个小孩在15分钟内出生的概率是多少？

指数分布的CDF可以写作：

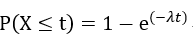
其中t为时间长度，e为自然底数。

下面用C++实现：

#include <iostream>

#include <cmath>

#include <iomanip>

double calc_exponential(double lambda, double t)

{

  double result;

  result = (1 - exp((-lambda) * t));

  return result;

}

int main()

{

  std::cout << std::fixed << std::setprecision(8) << calc_exponential(3, 0.25) << std::endl;

}

结果为：0.52763345

用Python验证：

import numpy as np

from scipy import stats

import matplotlib.pyplot as plt

def calc_expon():

    lambd = 3

    x = np.arange(0,1,0.25)

    y = 1 - np.exp(-lambd *x)

    print y

calc_expon()

结果为：[ 0.          0.52763345  0.77686984  0.89460078]

其中x=0.25时结果为0.52763345

下面是生成lambda=3的指数分布随机数，样本数是10000。同样是用C++实现，Python验证。

C++实现：

#include <iostream>

#include <cmath>

#include <iomanip>

#include <vector>

#include <cstdlib>

#include <ctime>

double calc_exponential(double lambda)

{

  double expon_rand = 0.0;

  while(1)

  {

    expon_rand = ((double)rand()/(double)RAND_MAX);

    if(expon_rand != 1)

    {

      break;

    }

  }

  expon_rand = ((-1 / lambda) * log(1 - expon_rand));

  return expon_rand;

}

int main()

{

  int t = 10000;

  double lambda = 3;

  const int distribution = 20;

  double dist_cells[distribution] = {0};

  srand((unsigned)time(NULL));

  for(int i = 0; i < t; i++)

  {

    int n = calc_exponential(lambda);

    dist_cells[n]++;

  }

  for(int i = 0; i < distribution; i++)

  {

    std::cout << dist_cells[i] << ",";

  }

  std::cout << std::endl;

  return 0;

}

结果是：9515,469,16,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,

放入Python并用Python生成的对比：

import numpy as np

from scipy import stats

import matplotlib.pyplot as plt

def gen_expon_rvs():

    cpp_result = np.array([9515,469,16,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0])

    lambd_recip = 0.33

    py_result = stats.expon.rvs(scale=lambd_recip,size=10000)

    plt.plot(cpp_result,color='r')

    plt.hist(py_result,color='b')

    plt.xlim(0,20)

    plt.show()

gen_expon_rvs()

得到图片：

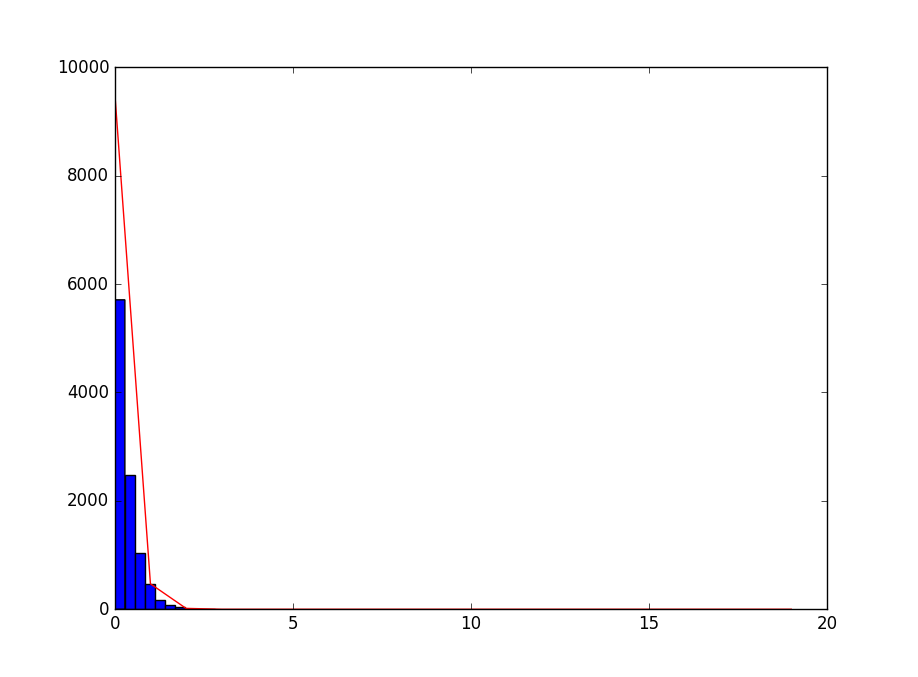
PS：其中最大值不一致的情形并不是计算错误，而是X轴的分布单位不一致，Python的是浮点的，而C++的代码是整形的，所以看到Python的分布最大值比较小是因为平均到了小数。

正态分布（高斯分布）

翻开任何一本讲统计的数学书，对于正态分布大抵会有相似的描述：若一个随机变量X服从一个数学期望为λ，标准差为σ的概率分布，且PDF为：

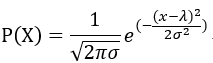
则称这个随机变量为正态随机变量。

当λ=0，σ=1时，称其为标准正态分布，PDF简化为：

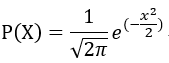
在现实中，有大量的案例是符合正态分布的，比如全中国18岁以上男性人口的身高分布，170cm左右的占绝大部分，160和180的占较少部分，150以下和190以上的占极少部分。

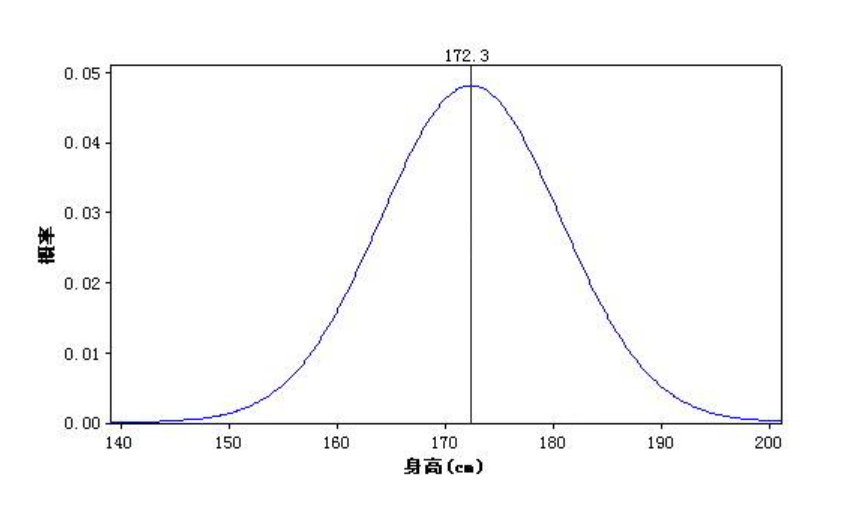
说起正态分布的例子，有个著名的实验是不得不提的，那就是高尔顿钉板实验。

高尔顿钉板是在一块竖起的木板上钉上一排排互相平行、水平间隔相等的铁钉，并且每一排钉子数目都比上一排多一个，一排中各个钉子下好对准上面一排两上相邻铁钉的正中央。从入口处放入一个直径略小于两颗钉子间隔的小球，当小球从两钉之间的间隙下落时，由于碰到下一排铁钉，它将以相等的可能性向左或向右落下，接着小球再通过两钉的间隙，又碰到下一排铁休。如此继续下去，小球最后落入下方条状的格子内。在等可能性（即小球落在左边和落在右边的概率均为50%）的情况下，小球落下后满足正态分布。

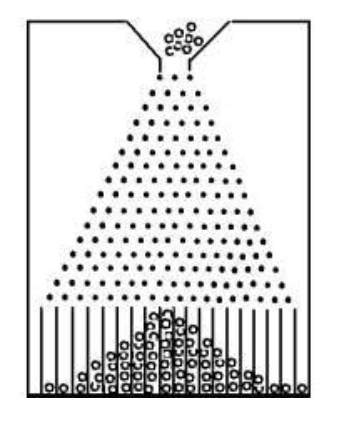
下面的代码用C++计算模拟高尔顿实验过程，并把结果放到Python显示出来。

C++模拟实验过程：

#include <iostream>

#include <cmath>

#include <iomanip>

#include <vector>

#include <cstdlib>

#include <ctime>

int binary_random()

{

  double rand_number = (rand() / (double)RAND_MAX);

  if(rand_number > 0.5)

    return 1;

  else return 0;

}

void galton_test(int num_of_cells, int num_of_balls)

{

  srand((unsigned)time(NULL));

  std::vector< int > cells(num_of_cells);

  int rand;

  for(int i = 1; i <= num_of_balls; i++)

  {

    int cell = 0;

    for(int j = 1; j < num_of_cells; j++)

    {

      int rand = binary_random();

      cell += rand;

    }

    cells[cell]++;

  }

  std::cout << std::endl;

  for(int i = 0; i < num_of_cells; i++)

  {

    std::cout << cells[i] << ",";

  }

  std::cout << std::endl;

}

int main()

{

  galton_test(20, 5000);

}

结果为：0,0,3,14,45,95,264,481,720,886,911,741,452,240,95,45,6,1,1,0,

结果每次都不一样，但将其放入以下Python代码显示：

import numpy as np

from scipy import stats

import matplotlib.pyplot as plt

def show_galton():

    n = np.array([0,0,3,14,45,95,264,481,720,886,911,741,452,240,95,45,6,1,1,0])

    plt.plot(n)

    plt.show()

show_galton()

得到以下图片：

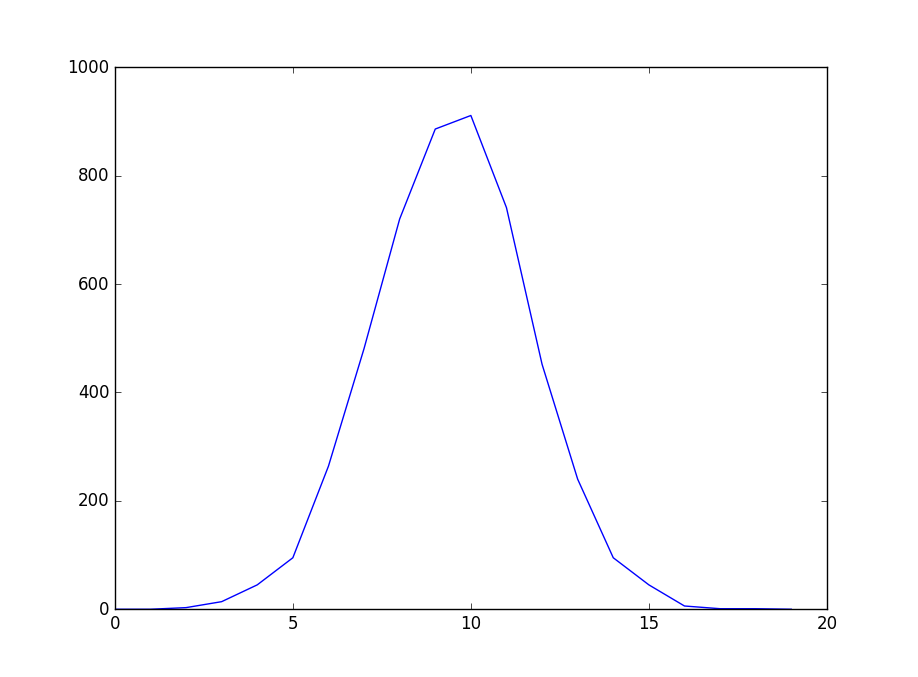
可以看出，是个明显的钟型曲线，说明高尔顿实验是满足正态分布的。在这个实验中，我们还可以去调整num_of_cells, num_of_balls的值，可以看出，当num_of_cells的值越大，曲线越陡峭，越小，曲线越平坦；num_of_balls的值越大，曲线就越像正态分布。说到这里可能大家就会想的到，这个实验中，num_of_cells的值可以认为就是正态分布的σ，而我们设定的随机数0，1会影响到正态分布的λ，有兴趣的朋友可以改一下上面的例程，将随机数生成改为大于0.5，或小于0.5，可以观察到最后的曲线中轴线会向左偏和向右偏。

说到这里，下面的公式应该是理所当然的了：

若一个随机变量X服从一个数学期望为λ，尺度参数为σ的概率分布，记作

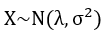
说到这里，通过上面的实验大家应该大概知道高斯分布是个什么东西了。那么如何编程实现生成符合高斯分布的随机数呢？

生成高斯分布的随机数有多种方法：

（1）     Box-Muller变换算法

（2）     利用中心极限定理迭代法

（3）     Ziggurat算法

等。其中，在效率和通用性方面比较均衡的是Box-Muller算法，C++11和Python的数学库里面基本都是用的它。

它的原理是：

随机抽出从[0,1]中符合均匀分布的数a和b，然后令：

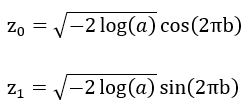
那么这两个数都是符合正态分布的。

若想产生服从期望是λ，标准差是σ的正态分布，那么：

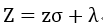
下面，我们用C++来实现：

#include <iostream>

#include <cmath>

#include <iomanip>

#include <vector>

#include <cstdlib>

#include <ctime>

#include <limits>

double calc_gaussian(double sigma, double lambda)

{

  static const double epsilon = std::numeric_limits<double>::min();

  static const double two_pi = (2.0 * 3.14159265358979323846);

  static double z1;

  static bool generate;

  generate = !generate;

  if (!generate)

    return z1 * sigma + lambda;

  double a, b;

  do

  {

    a = rand() * (1.0 / RAND_MAX);

    b = rand() * (1.0 / RAND_MAX);

  }while ( a <= epsilon );

  double z0;

  z0 = sqrt(-2.0 * log(a)) * cos(two_pi * b);

  z1 = sqrt(-2.0 * log(a)) * sin(two_pi * b);

  return z0 * sigma + lambda;

}

int main()

{

  int t = 10000;

  double lambda = 10;

  double sigma = 1;

  const int distribution = 20;

  double dist_cells[distribution] = {0};

  srand((unsigned)time(NULL));

  for(int i = 0; i < t; i++)

  {

    int n = calc_gaussian(sigma, lambda);

    dist_cells[n]++;

  }

  for(int i = 0; i < distribution; i++)

  {

    std::cout << dist_cells[i] << ",";

  }

  std::cout << std::endl;

  return 0;

}

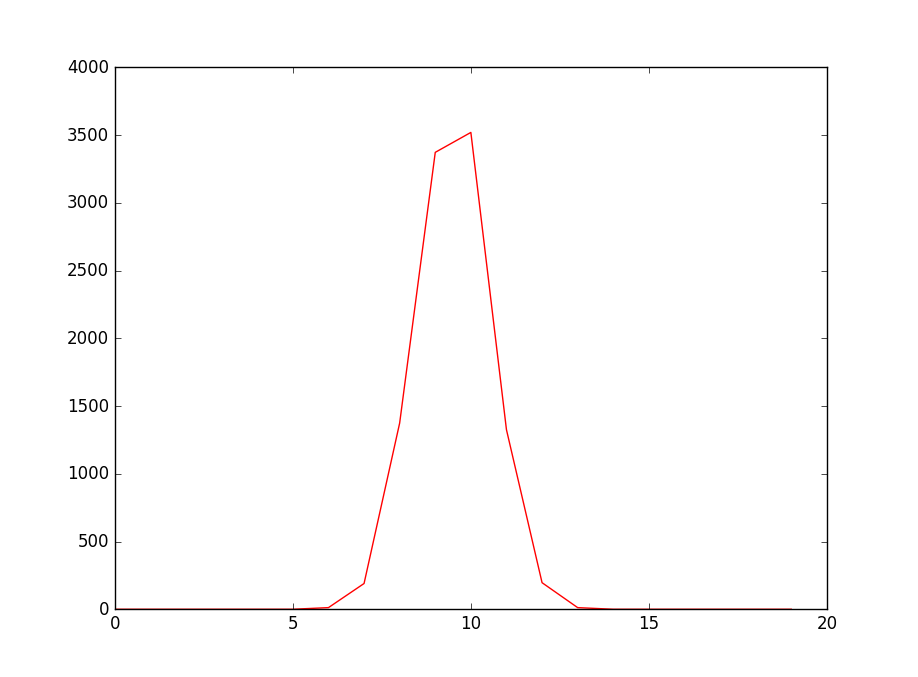
得到结果：0,0,0,0,0,0,12,190,1374,3372,3519,1325,196,12,0,0,0,0,0,0,

放入Python显示：

最新文章

  1. 利用jquery.validate以及bootstrap的tooltip开发气泡式的表单校验组件
  2. Mac下输入法总是默认中文，怎么设置成英文的？
  3. EF 自测例子
  4. 什么是javascript-SourceMap
  5. Linear Predictors
  6. XAML 概述三
  7. VS2010 win7 64位安装后新建项目生成时错误:LINK : fatal error LNK1123: 转换到 COFF 期间失败: 文件无效或损坏
  8. 关于 linux中TCP数据包(SKB)序列号的小笔记
  9. Android 个人手机通讯录开发
  10. Mac下R语言环境搭建
  11. Python的循环导入问题
  12. CentOS6.5安装pip
  13. Docker Macvlan 应用部署
  14. AngularJS 的常用特性（三）
  15. 动画中的id与class使用css3的优先级问题
  16. Spring data JPA 理解(默认查询 自定义查询 分页查询)及no session 三种处理方法
  17. element,点击查看，实现tab切换：
  18. mysql-cluster集群（亲测）
  19. 【leetcode刷题笔记】Jump Game
  20. IronPython for ASP.NET 部署注意事项

热门文章

  1. AI 芯片的分类及技术
  2. MindSpore算子支持类
  3. 分布式深度学习DDL解析
  4. 0算法基础学算法 搜索篇第二讲 BFS广度优先搜索的思想
  5. 2、java基础语法（上）：变量与运算符
  6. 【NX二次开发】缝合片体例子UF_MODL_create_sew
  7. spring boot使用@Async异步注解
  8. Java编程技巧：if-else优化实践总结归纳
  9. Jenkins CI&amp;CD 自动化发布项目实战(上篇)
  10. 20、nginx之ngx_http_upstream_module模块