斐波那契数列的三种C++实现及时间复杂度分析
本文介绍了斐波那契数列的三种C++实现并详细地分析了时间复杂度。
斐波那契数列定义:F(1)=1, F(2)=1, F(n)=F(n-1) + F(n-2) (n>2)
如何计算斐波那契数 F(n) 及时间复杂度 T(n) 呢?
我参考了一些资料总结了以下3种方法:递归法、顺序法和矩阵乘法,并给出了基于C++的简单代码实现和时间复杂度分析。
如有不当,欢迎指正。
方法1:递归法
实现:
#include <stdio.h>
#include <iostream> using namespace std; long long Fibonacci1(int n)
{
if (n < )
{
return ;
}
if (n == || n == )
{
return ;
}
return Fibonacci1(n - ) + Fibonacci1(n - );
}
int main()
{
char cont = 'y';
int n = ;
long long f = ;
cout << "Enter an integer:" << endl;
while (cin >> n)
{
f = Fibonacci1(n);
cout << "Fibonacci1(" << n << ") = " << f << endl;
cout << "Continue(y or n)?" << endl;
cin >> cont;
if (cont == 'y' || cont == 'Y')
{
cout << "Enter an integer:" << endl;
}
else
break;
}
return ;
}
时间复杂度:
设计算F(n)时调用递归的次数为call(n),T(n) = O(call(n))。
1. 数学归纳法(没兴趣的可以直接看下面的方法2)
当n = 1, 2时,F(n) = 1,call(n) = 1,T(n) = O(1)
当n > 2时,F(n) = F(n-1) + F(n-2),call(n) = call(n-1) + call(n-2) + 1(执行加法运算)。
n = 3时,call(3) = call(2) + call(1) + 1 = 3
n = 4时,call(4) = call(3) + call(2) + 1 = 5
n = 5时,call(5) = call(4) +call(3) + 1 = 9
……
注意到:F(3) = 2,call(3) = 3
F(4) = 3,call(4) = 5
F(5) = 5,call(5) = 9
由此猜测call(n) = 2 * F(n) - 1,下面用数学归纳法证明:
当n = 3时,等式成立。
假设n = k(k ≥ 3) 等式成立,即有:
call(k) = 2 * F(k) - 1
当n = k + 1时,
F(k+1) = F(k) + F(k-1)
call(k+1) = call(k) + call(k-1) + 1 = 2 * F(k) - 1 + 2 * F(k-1) -1 + 1 = 2 * F(k+1) - 1
所以,当n = k + 1时,等式也成立。
综上,call(n) = 2 * F(n) - 1 对 n ≥ 2都成立
所以,计算F(n)的时间复杂度T(n) = O(2 * F(n) - 1) = O(F(n)) ,
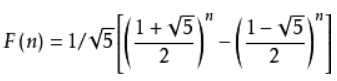
T(n)近似为O(2n)。
F(n)的计算可以参考“斐波那契数列”的百度百科:https://baike.baidu.com/item/%E6%96%90%E6%B3%A2%E9%82%A3%E5%A5%91%E6%95%B0%E5%88%97。
2. 二叉树法
观察以下二叉树:
f(5)
/ \
f(4) f(3)
/ \ / \
f(3) f(2) f(2) f(1)
/ \
f(2) f(1)
call(n)可以转化为求二叉树所有节点的个数。n = 5时,二叉树有4层,第一层有1个,第二层2个,第三层4个,第四层有2个。应用等比数列求和有call(n) = (1-2n-2)/(1-2) + 2 = 2n-2 + 1。T(n) = O(call(n)) = O(2n-2 + 1) = O(1/4 * 2n + 1) = O(2n)。
方法2:顺序法(从左到右依次求)
实现:
#include <stdio.h>
#include <iostream> using namespace std; long long Fibonacci2(int n)
{
long long temp1 = ;
long long temp2 = ;
long long result = ; if (n < )
{
return ;
}
if (n == || n == )
{
return ;
}
for (int i = ; i <= n; i++)
{
result = temp1 + temp2;
temp1 = temp2;
temp2 = result;
}
return result;
} int main()
{
char cont = 'y';
int n = ;
long long f = ;
cout << "Enter an integer:" << endl;
while (cin >> n)
{
f = Fibonacci2(n);
cout << "Fibonacci2(" << n << ") = " << f << endl;
cout << "Continue(y or n)?" << endl;
cin >> cont;
if (cont == 'y' || cont == 'Y')
{
cout << "Enter an integer:" << endl;
}
else
break;
}
return ;
}
时间复杂度:
通过顺序计算求得第n项,时间复杂度T(n) = O(n)。
方法3:矩阵乘法
实现:
F(n) = F(n-1) + F(n-2)是一个二阶递推数列,可以用矩阵乘法的形式表示为:
[F(n), F(n-1)] = [F(n-1), F(n-2)] * [a, b; c, d]
带入n = 3, 4 可求出a = b = c = 1, d = 0。
递推可进一步得到[F(n), F(n-1)] = [F(2), F(1)] * [a, b; c, d]n-2 = [1, 1] * [1, 1; 1, 0]n-2,F(n)便迎刃而解。
简单介绍一下矩阵幂运算的实现过程。
矩阵幂运算:
以矩阵A的106次方为例,(106)10 = (1101010)2 = 21 + 23 + 25 + 26 = 2 + 8 + 32 + 64,所以,
A106 = A2 * A8 * A32 * A64,
计算过程:
- result = E (单位矩阵),A平方得A2 0
- result *= A2,A2平方得A4
- A4平方得A8 0
- result *= A8,A8平方得A16
- A16平方得A32 0
- result *= A32,A32平方得A64
- result *= A64,A64平方得A128
即106的二进制形式有多少位,就要调用平方运算几次,这个次数p其实满足:2p-1 ≤ n < 2p,即p ≈ log2(n),这样就将方法2中复杂度为O(n)的计算降到了O(log2(n))。
#include <stdio.h>
#include <iostream> using namespace std; enum Status { kValid = , kInvalid };
int g_nStatus = kValid; class Matrix
{
public:
Matrix(int rows, int cols); // 构建一个全零矩阵
int GetRows() const; // 返回矩阵行数
int GetCols() const; // 返回矩阵列数
long long **p; // 指针数组
private:
int rows_; // 矩阵行数
int cols_; // 矩阵列数
}; Matrix::Matrix(int rows, int cols) : rows_(rows), cols_(cols)
{
if (rows < || cols_ < )
{
cout << "Matrix error!\n";
g_nStatus = kInvalid;
return;
}
// 分配空间
p = new long long *[rows_];
for (int i = ; i < rows_; i++)
{
p[i] = new long long[cols_];
}
// 初始化
for (int i = ; i < rows_; i++)
{
for (int j = ; j < cols; j++)
{
p[i][j] = ;
}
}
}
int Matrix::GetRows() const
{
return rows_;
}
int Matrix::GetCols() const
{
return cols_;
} // 矩阵乘法运算
Matrix MatrixMultiply(Matrix& m1, Matrix& m2)
{
Matrix result(m1.GetRows(), m2.GetCols());
if (m1.GetCols() == m2.GetRows())
{
for (int i = ; i < result.GetRows(); i++)
{
for (int j = ; j < result.GetCols(); j++)
{
for (int k = ; k < m1.GetCols(); k++)
{
result.p[i][j] += m1.p[i][k] * m2.p[k][j];
}
}
}
g_nStatus = kValid;
}
return result;
} // 矩阵幂运算
Matrix MatrixPowder(Matrix& m, int p)
{
g_nStatus = kInvalid;
Matrix result(m.GetRows(), m.GetCols());
if (m.GetRows() == m.GetCols())
{
for (int i = ; i < result.GetRows(); i++)
{
result.p[i][i] = ;
}
for (; p != ; p >>= )
{
if ((p & ) != )
{
result = MatrixMultiply(result, m);
}
m = MatrixMultiply(m, m);
}
}
return result;
} long long Fibonacci3(int n)
{
if (n < )
{
return ;
}
if (n == || n == )
{
return ;
}
Matrix m1(, );
m1.p[][] = ;
m1.p[][] = ;
m1.p[][] = ;
m1.p[][] = ; Matrix result = MatrixPowder(m1, n - );
if (g_nStatus == kInvalid)
{
cout << "Matrix error!\n";
return ;
}
return (result.p[][] + result.p[][]);
} int main()
{
char cont = 'y';
int n = ;
long long f = ;
cout << "Enter an integer:" << endl;
while (cin >> n)
{
f = Fibonacci3(n);
cout << "Fibonacci(" << n << ") = " << f << endl;
cout << "Continue(y or n)?" << endl;
cin >> cont;
if (cont == 'y' || cont == 'Y')
{
cout << "Enter an integer:" << endl;
}
else
break;
}
return ;
}
时间复杂度:
时间复杂度等于求矩阵n次方的复杂度,即O(log2n)。
总结:
三种方法的运行时间比较
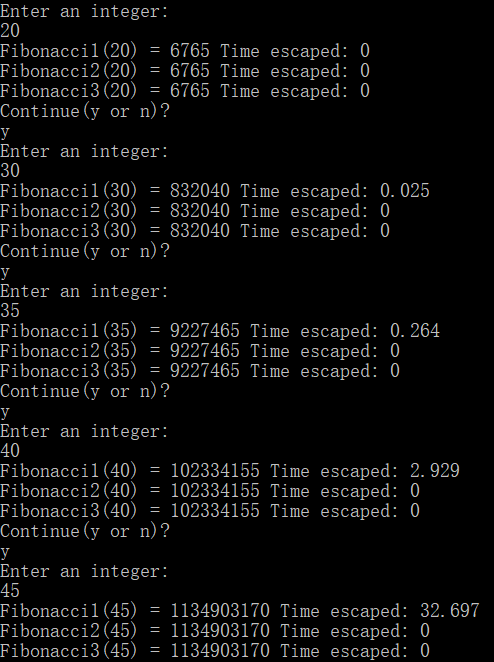
可以明显感受到方法1的呈指数增长的时间复杂度。
方法1太耗时,下面再比较方法2和方法3:
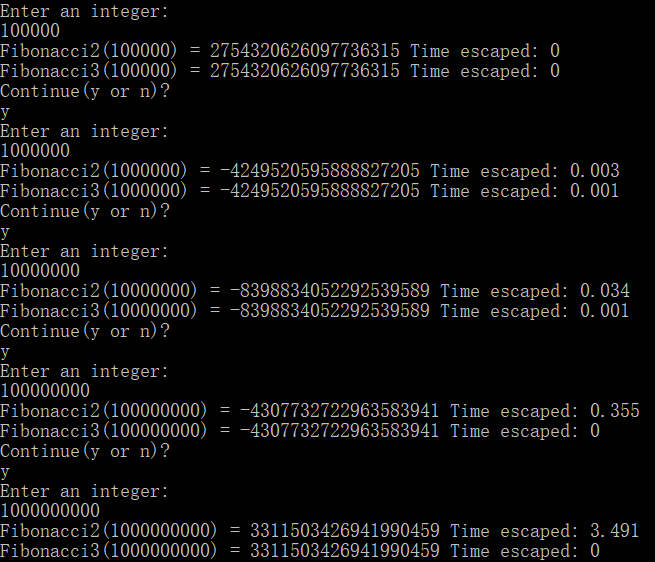
方法3秒杀方法2!
感悟
写完这篇随笔,深深体会到了算法的神奇。完成基本需求也许不难,又快又好的完成就需要有算法的功底啦。
最新文章
- t-sql或mssql怎么用命令行导入数据脚本
- 字符串&数组的相互转换
- Deep Learning Workbench Installation Notes
- 正则表达式中的\b
- Pyhton开发【第五篇】:Python基础之杂货铺
- HDU 1256 图片8
- 在Linux下的找不同-打补丁
- python笔记2-数据类型:列表[List]常用操作
- java 标准输入输出System.in与System.out
- SDOI 2018 R2 游记
- Luogu 2762 太空飞行计划 / Libre 6001 「网络流 24 题」太空飞行计划 (网络流,最大流)
- bzoj1652 / P2858 [USACO06FEB]奶牛零食Treats for the Cows
- 无法对 数据库'XXXXX' 执行 删除,因为它正用于复制
- linux用户和组
- android实战开发02
- Navicat数据备份
- Unicode字符集和UTF-8, UTF-16, UTF-32编码
- hdu 2437(dfs)
- job源码分析
- 【数据库】python访问mysql