本篇内容来自于书籍《3D图形学基础：图形与游戏开发》，个人总结

1.数学背景与历史

笛卡尔数学由著名的法国哲学家、物理学家、生物学家、数学家"勒奈·笛卡尔"发明。

1.1 1D数学

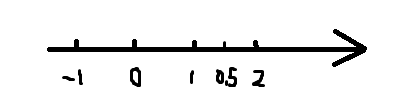
1.1.1 名词解释

整数：
1，2，3，4，50，-70
自然数：
非负整数，1，2，5，100。
有理数：
一个整数除以另一个整数，可以除尽，结果为，1/2、3/4/、0.88。
无理数：
有些数无法用有理数表示，如圆周长与直径的比值，记作π(pai)。小数点后有无穷的数，除不尽的数。
实数：
有理数 + 无理数的范围，有理数可数，无理数不可数。
离散数学：
研究自然数和整数的领域。
连续数学：
研究实数的领域。

1.2 2D数学

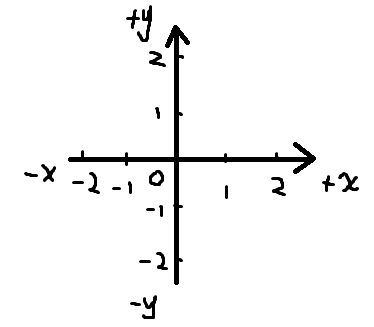
1.2.1 简单介绍

二维可以理解为矩形的网格。
高中时我们用的一般坐标系：横轴左-x，横轴右+x，纵轴上+y，纵轴下-y
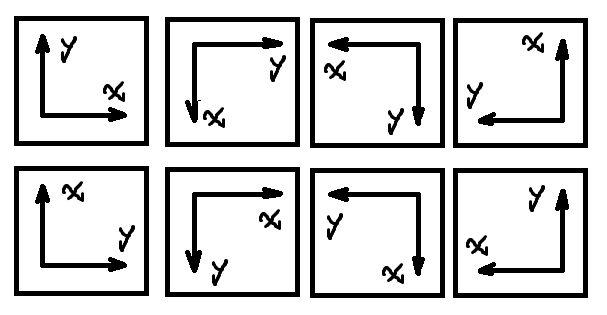
普通的坐标系，通过旋转变换，镜像变换，可以演化出8种坐标系，它们之间都是等价的。

1.3 3D数学：

1.3.1 2种三维坐标系

左手坐标系

左手坐标系：拇指指向+x，食指指向+y，中指指向+z（远离自己的方向）
右手坐标系

右手坐标系：拇指指向+x，食指指向+y，中指指向+z（远离自己的方向）
左手坐标系经过旋转变化有24种，右手一样也有24种，总共有48种坐标系
“左手坐标系” 与 “右手坐标系”不是等价的。

下文都用一般的左手坐标系

2.多坐标系统

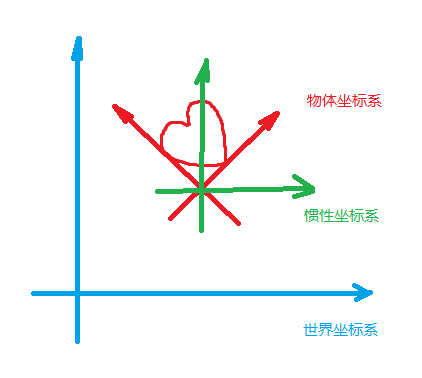
世界坐标系
物体坐标系
惯性坐标系
摄像机坐标系

3.向量

3.1 简单概念

向量：
“速度”和“位移”是向量，有大小有方向的量叫向量，向量描述位移。
标量：
“速率”和“长度”是标量，没有方向，向量的绝对值，标量描述数量。

3.2 向量的2种写法

一般用小写字母表示一个向量，比如 v。

行向量：
\(v=[2,3]\) (2D)
\(v=[5,-5,7]\) (3D)
\(v=[1,4,8,7]\) (4D)

可以省略逗号
\[v=\begin{bmatrix} 2&3 \end{bmatrix}\]
列向量：
\[v=\begin{bmatrix} 2\\3 \end{bmatrix}\]

注意：这2种写法没有优劣之分，一般情况下用“行向量”，因为书写方便

3.3 2D、3D、4D向量下标字母表示

2D:
\(v=[v_{x},v_{y}]\)

3D:
\(v=[v_{x},v_{y},v_{z}]\)

4D:
\(v=[v_{x},v_{y},v_{z},v_{w}]\) (w是分量)

3.4 向量的几何意义

二维向量\(v=[2,3]\)可以理解为，在二维坐标系中，从原点开始，先向+x走2步，再向+y走3步到终点，连接原点与终点。

三维向量\(v=[2,4,5]\)可以理解为，在三维坐标系中，从原点开始，先向+x走2步，再向+y走4步，再向+z走5步，连接原点与终点。

向量相当于表示，位移的序列。
向量与点：
“点”描述位置，\((2,3)\)是“点”，
“向量”描述位移，\([2,3]\)是“向量”。

4.向量运算

4.1 零向量

可以理解为“没有位移”，标量零表示“没有数量”

4.2 向量变负

几何上可以理解为，向量的方向相反，2D,3D,4D坐标系的操作分别是

\(-v=-[x,y]=[-x,-y]\)
\(-v=-[x,y,z]=[-x,-y,-z]\)
\(-v=-[x,y,z,w]=[-x,-y,-z,-w]\)

4.3 求模运算

求模运算，也就是求向量的大小，向量大小也称为“向量长度”，或“模”。比如有个向量 \(v\)，向量标量的绝对值两边加单数线，就是向量长度，记作"\(\begin{Vmatrix}v\end{Vmatrix}\)"

公式：
\(\begin{Vmatrix}v\end{Vmatrix}=\sqrt{v_{x}^{2}+v_{y}^{2}}\) (2D)
\(\begin{Vmatrix}v\end{Vmatrix}=\sqrt{v_{x}^{2}+v_{y}^{2}+v_{z}^{2}}\) (3D)

几何意义：2D的坐标系中，可以用勾股定理解释；3D的证明很复杂，不讨论。

4.4 标量与向量的乘法（除法）：

公式：

乘法
\(kv=k[v_{x},v_{y}]=[kv_{x},kv_{y}]\) (2D)
\(kv=k[v_{x},v_{y},v_{z}]=[kv_{x},kv_{y},kv_{z}]\) (3D)

除法
\[\frac{1}{k}=\frac{1}{k}[v_{x},v_{y}]=[\frac{1}{k}v_{x},\frac{1}{k}v_{y}]\]

\[\frac{1}{k}=\frac{1}{k}[v_{x},v_{y},v_{z}]=[\frac{1}{k}v_{x},\frac{1}{k}v_{y},\frac{1}{k}v_{z}]\]

4.5 标准化向量

标准化向量一般用向量名\(v\)，加下标norm组成，记作“ \(v_{norm}\) ”，这个过程称为“标准化”。
公式：
\(v_{norm}=v/\begin{Vmatrix}v\end{Vmatrix}\)

举个例子：
\[v=[12,5]\\v_{norm} =\frac{[12,5]} {\begin{Vmatrix}[12,5]\end{Vmatrix}}\\=\frac{[12,5]}{\sqrt{12^2+5^2}} \\
=\frac{[12,5]}{13}\\
\approx[0.923,0.385]\]

几何意义：可以从上面的例子中看出，在2D中的标准化后的向量是一个从原点出发，模为1的向量。

4.6 向量加减法

向量\(a\)与向量\(b\)相加时，可以理解为，A的终点接到B的起点，接着从A的起点指向B的终点就是两向量相加的结果；向量\(a\)与向量\(b\)在相减时，可以理解为，B的终点指向A的终点的向量就是两向量相减的结果。
（图）

公式：
\(a+b=[a_{x},a_{y}]+[b_{x},b_{y}]=[a_{x}+b_{x},a_{y}+b_{y}]\) (2D)
\(a-b=[a_{x},a_{y}]-[b_{x},b_{y}]=[a_{x}-b_{x},a_{y}-b_{y}]\) (2D)
\(a+b=[a_{x},a_{y},a_{z}]+[b_{x},b_{y},b_{z}]=[a_{x}+b_{x},a_{y}+b_{y},a_{z}+b_{z}]\) (3D)
\(a-b=[a_{x},a_{y},a_{z}]-[b_{x},b_{y},b_{z}]=[a_{x}-b_{x},a_{y}-b_{y},a_{z}-b_{z}]\) (3D)

注意：

向量加法满足交换律，向量减法不满足交换律
永远有\(a+b=b+a\)
但\(a-b=-(b-a)\)仅当\(a=b\)时，\(a-b=b-a\)

4.7 两点间距离公式

公式：
\(距离(a,b)=\sqrt{(b_{x}-a_{x})^2+(b_{y}-a_{y})^2}\) (2D)
\(距离(a,b)=\sqrt{(b_{x}-a_{x})^2+(b_{y}-a_{y})^2+(b_{z}-a_{z})^2}\) (3D)

4.8 向量点乘

也称作“内积”，结果在几何中表示2个向量的“相似”程度，\(a\)点乘\(b\)，记作“ \(a·b\) ”，点不能省略，结果是其夹角的cos值，若结果>0，则夹角\(0<=\theta<90\)；若结果=0，则夹角\(\theta\)=90；若结果<0，则夹角\(\theta\)>90

公式1：
\(a·b = a_{x}b_{x} + a_{y}b_{y}\) (2D)
\(a·b = a_{x}b_{x} + a_{y}b_{y}+a_{z}b_{z}\) (2D)

公式2：
\(a·b = ||a|| \quad ||b||\quad \cos { (\theta )}\)

有用的推导：用点乘计算2个向量的夹角

\[\theta = \arccos{( \frac{a·b}{\begin{Vmatrix}a\end{Vmatrix}\begin{Vmatrix}b\end{Vmatrix}})}\]

4.9 向量投影

求向量\(v\)在向量\(n\)上的投影，能将\(v\)分解为两个分量：\(v_{\bot}\)和\(v_{\vert\vert}\)。他们分别垂直于和平行于\(n\)，并满足\(v=v_{\bot}+v_{\vert\vert}\)。一般称平行分量\(v_{\vert\vert}\)为\(v\)在\(n\)上的投影。

\[v_{平行}=v_{\vert\vert}= n\frac{v·n}{\begin{Vmatrix}n\end{Vmatrix}^2}\]
\[v_{垂直}=v_{\bot}= \begin{Vmatrix}v\end{Vmatrix}-n\frac{v·n}{\begin{Vmatrix}n\end{Vmatrix}^2}\]

4.10 向量叉乘

又称作“叉积”，叉乘的结果是一个向量，该向量垂直于2个叉乘向量组成的平面

公式1：
\(a=[a_{x},a_{y},a_{z}]\)
\(b=[b_{x},b_{y},b_{z}]\)
\(a\times b=[(a_{y}b_{z}-a_{z}b_{y}),(a_{z}b_{x}-a_{x}b_{z}),(a_{x}b_{y}-a_{y}b_{x})]\)

向量叉乘后向量的长度，为2向量的夹角θsin值与2向量长度的积，这个长度也是a和b向量组成平行四边形的面积

公式2：
\(\begin{Vmatrix}a\times b\end{Vmatrix} = \begin{Vmatrix}a\end{Vmatrix}\begin{Vmatrix}b\end{Vmatrix}\sin{(\theta)}\)

叉乘结果向量的方向
在左手坐标系中，若叉乘的两向量收尾相接后是顺时针，则指向你；若叉乘的两向量收尾相接后是逆时针，则远离你；右手坐标系则相反

5.Vector3类型

关于这个类型的实现，每一种语言都有不同的实现方式，从书中看到的结果是，定义了Vector3类有自己的构造方法，并且对常用的运算符进行重载，加了一些常用方法。

我相信，在unity中的Vector3也有相应的操作，比如点乘操作用方法来表现，而不是去重载“*”算符。

这个类基本上游戏引擎都会实现。

巴特西

3D图形学常用公式