题解:UVa1025 A Spy in the Metro
2024-09-07 01:11:53
题目大意
给出一张无向图图,求该图的最小瓶颈生成树。
无向图的瓶颈生成树:无向图\(G\)的一颗瓶颈生成树是这样的一颗生成树:它最大的边权值在\(G\)的所有生成树中是最小的。瓶颈生成树的值为\(T\)中最大权值边的权。
该图建立在坐标系中, 给出每个点的坐标。任意两点之间都有边,边权即为两点间的距离。
题解
由于只关心生成树的最大值,我们可以将边从小到大排序,依次加入(若构成环则不加入),直到构成一颗生成树。
相信你已经发现了:这不就是Kruskal算法吗?
于是,我们得出结论:无向图的最小生成树一定是瓶颈生成树。
如果你仍然感到怀疑,那么我们再用反证法证明:
假设存在一张无向图的最小生成树\(T\)不是瓶颈生成树,那么我们找到该最小生成树的权值最大边\(e\),我们选取该图中的一颗瓶颈生成树\(T_1\),则有:对于\(T_1\)中的任何边\(e_1\),存在\(V_{e_1} <V_{e}\)。删除\(T\)中的\(e\),我们得到两棵树\(T_a,T_b\)。由于\(T_1\)是一颗生成树,必有一条边\(e_{ab}\)连接\(T_a,T_b\),用\(e_{ab}\)替换\(e\),可以得到更小的生成树,与\(T\)是最小生成树矛盾。证毕。
顺便提一句,无向图瓶颈生成树一定是最小生成树吗?
看一看下图就知道了:
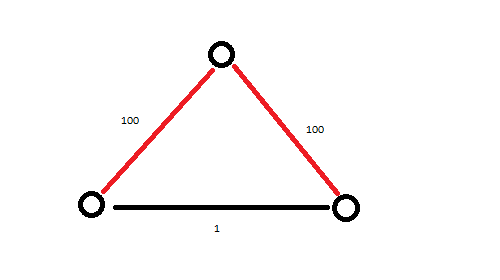
由于本题是稠密图,最好用Prim解决(然而懒到家的我还是用了Kruskal)。
听说有一种复杂度更优的算法叫Camerini's algorithm(然而我并不会),如果有大神会的话也可以教导我一下。
代码
#include <cstdio>
#include <cmath>
#include <algorithm>
using namespace std;
const int maxn = 5005;
struct City
{
double x, y;//注意是小数(开float似乎也行)
} city[maxn];
struct Edge
{
int from, to;
double dist;
bool operator < (const Edge& other) const
{
return dist < other.dist;
}
} edge[maxn*maxn];
int n, m, S;
inline double sqr(double a)
{
return a*a;
}
inline double make_dist(City a, City b)
{
return sqrt(sqr(a.x-b.x) + sqr(a.y-b.y));
}
inline void add_edge(City a, City b, int ai, int bi)
{
double dist = make_dist(a, b);
m++;
edge[m].from = ai;
edge[m].to = bi;
edge[m].dist = dist;
}
inline void read()
{
scanf("%d%d", &S, &n);
S = n-S;
for(int i = 1; i <= n; ++i)
{
scanf("%lf%lf", &city[i].x, &city[i].y);
for(int j = 1; j < i; ++j)
add_edge(city[i], city[j], i, j);
}
}
struct UN_set
{
int fa[maxn];
inline void init(int n)
{
for(int i = 1; i <= n; ++i)
fa[i] = i;
}
inline int getfa(int x)
{
return fa[x] == x ? x : fa[x] = getfa(fa[x]);
}
} un;
inline double Kruskal()//其实最好还是用prim
{
int tmp = 0;
m = 0;
read();
sort(edge+1, edge+m+1);
un.init(n);
for(int i = 1; i <= m; ++i)
{
int ff = un.getfa(edge[i].from);
int tf = un.getfa(edge[i].to);
if(ff != tf)
{
un.fa[ff] = tf;
tmp++;
if(tmp == S)
return edge[i].dist;
}
}
return -1;
}
int main()
{
int nnn;
scanf("%d", &nnn);
while(nnn--)
printf("%.2f\n", Kruskal());//直接求最小生成树即可
return 0;
}
最新文章
- PHP获取当前位置
- modelsim仿真vivado自动化脚本
- 详解SQL集合运算
- Linux常用命令(转)
- Lucene.Net的服务器封装+APi组件 (开源)
- Android学习之路书籍推荐
- go gomail
- Python学习(3)变量类型
- skyline TerraExplorer fly设置相对路径的方法
- mysql数据库时间、字符串类型互转
- angularJs 使用中遇到的问题小结【一:关于传参】
- Linux command not found 问题解释
- LOW版统计词频
- 仓位管理 V4.3
- Python闭包举例
- freemarker使用
- 网络流n题
- PLSQL 使用技巧汇总贴(一个坑)
- Php实现版本比较接口
- 面试题思考:GET和POST两种基本请求方法的区别