清明 DAY 1
2024-10-11 22:54:06
数学基础
Part 1. 高精度计算
Part 2. 模意义下的运算
mod
对一个数取模,其实就是取余数
注意:
• 无除法运算
• 满足基本的交换律、分配率、结合律
Part 4. 费马小定理与GCD&LCM
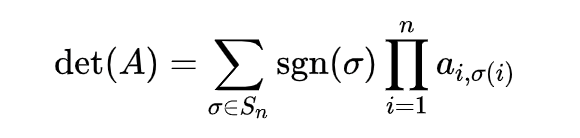
Part 5. 素数与筛法
Part 6. 欧拉函数
行列式
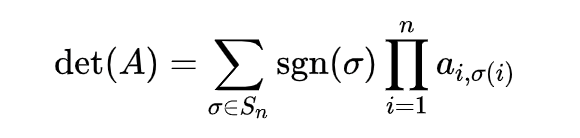
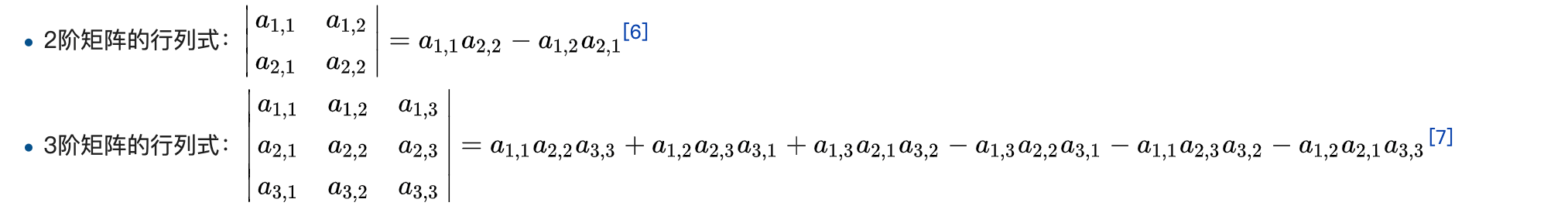
行列式计算:
1.利用高斯消元将原矩阵变为对角矩阵
2.将对角线上的值连乘得到行列式
矩阵逆元
逆元的定义:
若矩阵B*A=I 则称B为A的左逆元
若矩阵A*B=I 则称B为A的左逆元
有逆元的前提:
矩阵行列式不为0
LH的矩阵求逆板子:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#define LL long long
#define N 405
using namespace std;
const int mod=1e9+7; template<class T>inline void rd(T &x){
x=0; short f=1; char c=getchar();
while(c<'0' || c>'9') f=c=='-'?-1:1,c=getchar();
while(c<='9' && c>='0') x=x*10+c-'0',c=getchar();
x*=f;
} int n,m;
int f[N][N<<1],r,ans; inline int qpow(int x,int k){
int ret=1;
while(k){
if(k&1) ret=1LL*ret*x%mod;
x=1LL*x*x%mod; k>>=1;
} return ret;
} inline void Gauss(){
for(int i=1;i<=n;i++){
for(int j=i;j<=n;j++)
if(f[j][i]){
if(j!=i) for(int k=1;k<=m;k++) swap(f[i][k],f[j][k]);
break;
}
if(!f[i][i]){puts("No Solution");exit(0);}
r=qpow(f[i][i],mod-2);
for(int j=i;j<=m;j++) f[i][j]=1LL*f[i][j]*r%mod;
for(int j=1;j<=n;j++)
if(j!=i){
r=f[j][i];
for(int k=i;k<=m;k++)
f[j][k]=(f[j][k]-1LL*r*f[i][k]%mod+mod)%mod;
}
}
for(int i=1;i<=n;i++){
for(int j=n+1;j<=m;j++) printf("%d ",f[i][j]);
puts("");
} return;
} int main(){
rd(n); m=n<<1;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++) rd(f[i][j]);
f[i][n+i]=1;
}
Gauss();
return 0;
}
扩充知识
然而后面这些知识点LH貌似没讲
矩阵树定理
一个图的邻接矩阵G:对于无向图的边(u,v),G[u][v]++,G[v][u]++
一个图的度数矩阵D:对于无向图的边(u,v),D[u][u]++,D[v][v]++
而通过这两个矩阵就可以构造出图G的基尔霍夫矩阵:C=D-G.
Matrix Tree定理:
将图G的基尔霍夫矩阵去掉第i行和第i列(i可以取任意值,可以证明所得到的结果相同),得到(n-1)*(n-1)的矩阵,对这个矩阵进行行列式的值求解,abs(det(A))即为图G的生成树个数。
有向图 - 矩阵树定理
树形图:以i点为根节点的树形图有(n-1)条边,从i节点出发可以到达其他所有(n-1)个节点.
定义: 有向图的邻接矩阵G:对于有向图的边(u,v),G[u][v]++.
有向图的度数矩阵D:对于有向图的边(u,v),D[v][v]++.
尤其需要注意的是:有向图的度数矩阵指的是一个点的入度,而不是出度。
而有向图的基尔霍夫矩阵的构造方式是一模一样的:C=D-G.
有向图Matrix Tree定理:
将有向图G的基尔霍夫矩阵去掉第i行和第i列,得到(n-1)*(n-1)的矩阵,对这个矩阵进行行列式的值求解,abs(det(A))就是以i为根的树形图的个数。
拓展:k^2logn求常系数线性递推方程
最新文章
- 解决ora-01652无法通过128(在temp表空间中)扩展temp段的过程
- oracle的decode函数在mysql的实现
- cookie 和session 区别
- 第一周 总结笔记 / 斯坦福-Machine Learning-Andrew Ng
- nginx php-fpm安装配置
- Oracle参数化查询
- 【转】【编码】ASCII 、UNICODE和UTF-8之二
- GitBook – 使用 GitHub 和 Markdown 制作书籍
- 金山快盘有Linux版了
- C语言第一节 C语言程序与开发工具
- android.support.v4.widget.DrawerLayout使用
- java 修饰符的作用一(public protected default private 组)
- C学习之指针强化
- python小游戏实现代码
- Visual Studio 单元测试之六---UI界面测试
- iOS CGRectContainsPoint的用法
- Python3.5学习笔记-列表、元组、字典
- Dom模型
- .bash_profile和.bashrc的什么区别及启动过程
- 【Python学习】yield send我就说这么多
热门文章
- HTML中--定义header和footer高度中间自适应
- SecureCRT乱码问题的解决
- 一个基于JRTPLIB的轻量级RTSP客户端(myRTSPClient)——实现篇:(九)以g711-mulaw为例添加新的编码格式解析支持
- 转: Java LinkedList基本用法
- python-lambda、filter、reduce、map
- (已解决)Eclipse报错:Could not find XXX.apk. 没有Android项目命名. There is no android project named
- 数据加密之SymmetricAlgorithm加密
- Unity中HideInInspector和SerializeField以及Serializable
- .NET Core使用Quartz执行调度任务进阶(转)
- end to end