Chapter 15 Outcome Regression and Propensity Scores

15.1 Outcome regression
15.2 Propensity scores
15.3 Propensity stratification and standardization
15.4 Propensity matching
15.5 Propensity models, structural models, predictive models
Fine Point
- Nuisance parameters
- Effect modification and the propensity score
Technical Point
- Balancing scores and prognostic scores

Hern\(\'{a}\)n M. and Robins J. Causal Inference: What If.

这一章讲一种新的方法: propensity scores.

15.1 Outcome regression

在满足条件可交换性下,

\[\mathbb{E} [Y^{a=1, c=0}|L=l] = \mathbb{E} [Y|A=1, C=0, L=l].
\]

之前的模型都是对等式左端进行建模, 倘若我们对等式右端进行建模呢?

\[\mathbb{E} [Y|A,C=0, L] = \alpha_0 + \alpha_1 A + \alpha_2 AL + \alpha_3L.
\]

15.2 Propensity scores

在IP weighting 和 g-estimation的使用过程中, 我们需要估计条件概率\(\mathrm{Pr}[A=1|L]\), 记为\(\pi (L)\).

\(\pi (L)\) 就是所谓的propensity scores, 其反应了特定\(L\)的一种倾向.

首先我们要证明,

\[Y^a \amalg A | L \Rightarrow Y^a \amalg A | \pi(L).
\]

不妨假设\(\pi(L) = s \Leftrightarrow L \in \{l_i\}\), 则

\[\begin{array}{ll}
\mathrm{Pr}[Y^a|\pi(L)=s]
&= \mathrm{Pr} [Y^a|L \in \{l_i\}] \\
&= \frac{\sum_i\mathrm{Pr}[Y^a,L=l_i]}{\sum_i \mathrm{Pr} [L=l_i]}\\
&= \frac{\sum_i\mathrm{Pr}[Y|A=a, L=l_i]\mathrm{Pr}[L=l_i]}{\sum_i \mathrm{Pr} [L=l_i]}\\
&= \frac{\mathrm{Pr}[A=a|L=l] \cdot \sum_i\mathrm{Pr}[Y|A=a, L=l_i]\mathrm{Pr}[L=l_i]}{\mathrm{Pr}[A=a|L=l]\sum_i \mathrm{Pr} [L=l_i]}\\
&= \frac{\cdot \sum_i\mathrm{Pr}[Y|A=a, L=l_i]\mathrm{Pr}[A=a, L=l_i]}{\sum_i \mathrm{Pr} [A=a, L=l_i]}\\
&= \frac{\cdot \sum_i\mathrm{Pr}[Y, A=a, L=l_i]}{\sum_i \mathrm{Pr} [A=a, L=l_i]}\\
&= \frac{\cdot \mathrm{Pr}[Y, A=a, \pi(L)=s]}{\mathrm{Pr} [A=a, \pi(L)]}\\
&= \mathrm{Pr} [Y|A=a, \pi(L)=s].
\end{array}
\]

注意: \(\pi(l_i) = \pi(l_j) = \pi(l) = s\).

注意到, 上面有很重要的一步, 我们上下同时乘以\(\mathrm{Pr}[A=a|L=l]\), 实际上只有当\(A \in \{0, 1\}\)的时候才能成立, 因为二元, 加之\(\pi(L)=s\), 所以

\[\mathrm{Pr}[A=a|L=l_i] = \mathrm{Pr}[A=a|L=l_j].
\]

也就是说当\(A\)不是二元的时候, 上面的推导就是错误的了.

怪不得书上说, propensity scores这个方法是很难推广的非二元treatments的情况的.

15.3 Propensity stratification and standardization

此时, 我们可以把\(\pi(L)\)看成一个新的中间变量\(L\)(confounder?), 如下图:

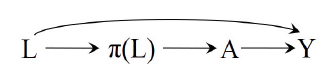
要知道, 原来的\(L\)可能是一个高维向量, 现在压缩为一维, 这意味着我们的可以将

\[\mathbb{E}[Y|A, C=0, \pi(L)]
\]

假设地更加精简.

估计或许更加牢靠(直接无参数模型?).

但是需要指出是, 不同个体的\(\pi(L)\)往往都是不同的, 这就导致我们想要估计

\[\mathbb{E} [Y|A=1, C=0|\pi(L)=s] - \mathbb{E} [Y|A=0, C=0|\pi(L)=s]
\]

几乎是不可能的.

一种比较好的做法是, 分成一段段区间, 考虑

\[\mathbb{E} [Y|A=1, C=0|\pi(L)\in \Delta_s] - \mathbb{E} [Y|A=0, C=0|\pi(L)\in \Delta_s].
\]

比如书上推荐的10分位.

当然这种做法会在一定程度上破化条件可交换性, 但是可以认为如果区间取得比较合适, 结果应该是比较合理的.

另外需要指出的, 我们往往会陷入一个误区, 觉得\(\pi(L)\), 即条件概率\(\mathrm{Pr}[A=1|L]\)的估计越准确越好, 实际上不是.

我们需要保证的仅仅是满足条件可交换性, 实际上准确度无关紧要.

有些时候过分追求准确度会适得其反, 因为这时我们往往会引入很多的变量, 导致我们的条件可交换性被大大破坏了.

所以不要仅仅当成是回归问题来看.

巴特西

Chapter 15 Outcome Regression and Propensity Scores

15.1 Outcome regression

15.2 Propensity scores

15.3 Propensity stratification and standardization

15.4 Propensity matching

15.5 Propensity models, structural models, predictive models

Fine Point

Nuisance parameters

Effect modification and the propensity score

Technical Point

Balancing scores and prognostic scores

最新文章

热门文章