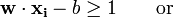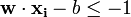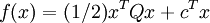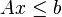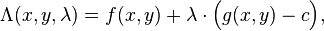数学之路(3)-机器学习(3)-机器学习算法-SVM[5]

svm小结

1、超平面

两种颜色的点分别代表两个类别，红颜色的线表示一个可行的超平面。在进行分类的时候，我们将数据点 x 代入 f(x) 中，如果得到的结果小于 0 ，则赋予其类别 -1 ，如果大于 0 则赋予类别 1 。如果 f(x)=0 ，则很难办了，分到哪一类都不是。事实上，对于 f(x) 的绝对值很小的情况，我们都很难处理，因为细微的变动（比如超平面稍微转一个小角度）就有可能导致结果类别的改变。理想情况下，我们希望 f(x) 的值都是很大的正数或者很小的负数，这样我们就能更加确信它是属于其中某一类别的。

超平面的数学形式可以写作

。

其中是超平面上的点，是垂直于超平面的向量。

根据几何知识，我们知道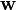向量垂直于分类超平面。加入位移b的目的是增加间隔。如果没有b的话，那超平面将不得不通过原点，限制了这个方法的灵活性。

2、点到超平面的距离

我们就可以定义一个样本点到某个超平面的间隔：

δ_i=y_i(wx_i+b)

这个公式乍一看没什么神秘的，也说不出什么道理，只是个定义而已，但我们做做变换，就能看出一些有意思的东西。

首先注意到如果某个样本属于该类别的话，那么wx_i+b>0（记得么？这是因为我们所选的g(x)=wx+b就通过大于0还是小于0来判断分类），而y_i也大于0；若不属于该类别的话，那么wx_i+b<0，而y_i也小于0，这意味着y_i(wx_i+b)总是大于0的，而且它的值就等于|wx_i+b|！

我们定义 functional margin 为

γˆ=y(wTx+b)=yf(x)

，注意前面乘上类别

之后可以保证这个 margin 的非负性。

对于一个点

x
，令其垂直投影到超平面上的对应的为

x0
，由于

w
是垂直于超平面的一个向量（请自行验证），我们有

x=x0+γw∥w∥

在

n
维的数据空间中找到一个超平面，其方程可以表示为

一个超平面，在二维空间中的例子就是一条直线，由于

x0
是超平面上的点，满足

f(x0)=0
，代入超平面的方程即可算出

γ=wTx+b∥w∥=f(x)∥w∥

||w||表示向量的模长，向量的模，即向量的长度

关于向量的相关计算:

这里的

γ
是带符号的，我们需要的只是它的绝对值，因此类似地，也乘上对应的类别

y
即可，因此实际上我们定义 geometrical margin 为：

γ˜=yγ=γˆ∥w∥

显然，functional margin 和 geometrical margin 相差一个

∥w∥
的缩放因子。

通过这个超平面可以把两类数据分隔开来，比如，在超平面一边的数据点所对应的

y
全是 -1 ，而在另一边全是 1 。具体来说，我们令

f(x)=wTx+b
，显然，如果

f(x)=0
，那么

x
是位于超平面上的点。

3、间隔(margin)的理解

点到超平面的距离定义为几何间隔 (geometricalmargin)

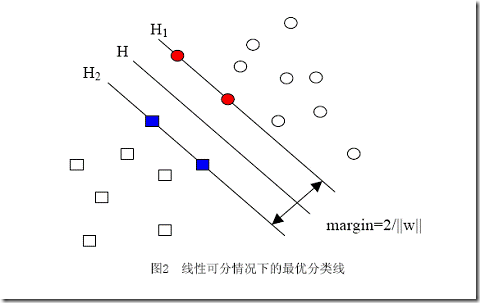
几何间隔，几何间隔所表示的正是点到超平面的欧氏距离，我们下面就简称几何间隔为“距离”。以上是单个点到某个超平面的距离（就是间隔，后面不再区别这两个词）定义，同样可以定义一个点的集合（就是一组样本）到某个超平面的距离为此集合中离超平面最近的点的距离。下面这张图更加直观的展示出了几何间隔的现实含义：

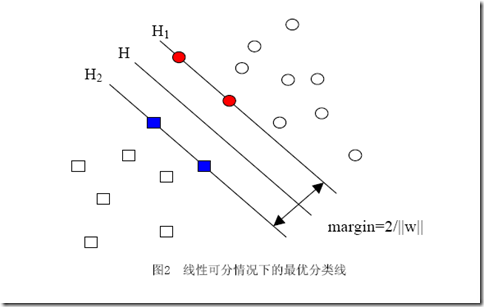
H
₁
与H，H
₂
与H之间的距离就是几何间隔。几何间隔越大的解，它的误差上界越小。因此最大化几何间隔成了我们训练阶段的目标

对于一个包含

n
个点的数据集，我们可以很自然地定义它的 margin 为所有这

n
个点的 margin 值中最小的那个。于是，为了使得分类的效果高，我们希望所选择的超平面能够最大化这个 margin 值。

样本点中margin 值中最小的那些就是落在2边直线上的点，2边直线中间就是空白

4、margin的目标

直接来解||w||最小值问题，很容易看出当||w||=0的时候就得到了目标函数的最小值。但是你也会发现，无论你给什么样的数据，都是这个解！反映在图中，就是H1与H2两条直线间的距离无限大，这个时候，所有的样本点（无论正样本还是负样本）都跑到了H1和H2中间，而我们原本的意图是，H1右侧的被分为正类，H2 左侧的被分为负类，位于两类中间的样本则拒绝分类（拒绝分类的另一种理解是分给哪一类都有道理，因而分给哪一类也都没有道理）

点到超平面的距离定义为 geometrical margin ，geometrical margin 因为除上了

∥w∥
这个分母，所以缩放

w
和

b
的时候

γ˜
的值是不会改变的，它只随着超平面的变动而变动，因此，这是更加合适的一个 margin 。这样一来，我们的 maximum margin classifier 的目标函数即定义为

maxγ˜

，还需要满足一些条件，根据 margin 的定义，我们有

yi(wTxi+b)=γˆi≥γˆ,i=1,…,n

其中

γˆ=γ˜∥w∥

在超平面固定的情况下，

γˆ
的值也可以随着

∥w∥
的变化而变化。由于我们的目标就是要确定超平面，因此可以把这个无关的变量固定下来，固定的方式有两种：一是固定

∥w∥
，当我们找到最优的

γ˜
时

γˆ
也就可以随之而固定；二是反过来固定

γˆ
，此时

∥w∥
也可以根据最优的

γ˜
得到。处于方便推导和优化的目的，我们选择第二种，令

γˆ=1
，则我们的目标函数化为：

∥w∥,s.t.,yi(wTxi+b)≥1,i=1,…,n

中间的红色线条是超平面，另外两条线到红线的距离都是等于

γ˜

5、最佳超平面

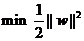不难看出当||w||²达到最小时，||w||也达到最小，所以最小化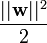就是最小化||w||

当||w||=0的时候就得到了目标函数的最小值，但所有样本点都进入了无法分类的灰色地带,因为描述问题的时候只考虑了目标，而没有加入约束条件，约束条件就是在求解过程中必须满足的条件,样本点必须在H1或H2的某一侧（或者至少在H1和H2上），而不能跑到两者中间。提到过把间隔固定为1，这是指把所有样本点中间隔最小的那一点的间隔定为1，也就意味着集合中的其他点间隔都不会小于1

为了使得样本数据点都在超平面的间隔区以外，我们需要保证对于所有的满足其中的一个条件

按照间隔的定义，满足这些条件就相当于让下面的式子总是成立：

y_i[(w·x_i)+b]≥1 (i=1,2,…,l) （l是总的样本数）

但我们常常习惯让式子的值和0比较，因而经常用变换过的形式：

y_i[(w·x_i)+b]-1≥0 (i=1,2,…,l) （l是总的样本数）

因此我们的两类分类问题也被我们转化成了它的数学形式，一个带约束的最小值的问题：

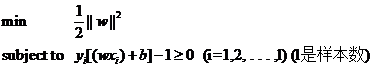
最佳超平面这个问题就变成了在以上约束条件下最小化|w|.这是一个二次规划QP(quadratic programming)最优化中的问题。

最小化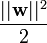，满足其中。

1/2这个因子是为了数学上表达的方便加上的。

6、凸二次规划

凸集，凸集是指有这么一个点的集合，其中任取两个点连一条直线，这条线上的点仍然在这个集合内部

二次规划问题可以以下形式来描述：

受到一个或更多如下型式的限制条件：

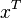是的转置。

可总结为下面的约束优化问题:

7、求解

我们想求得这样一个线性函数（在n维空间中的线性函数）：

g(x)=wx+b

使得所有属于正类的点x₊代入以后有g(x₊)≥1，而所有属于负类的点x_-代入后有g(x_-)≤-1（之所以总跟1比较，无论正一还是负一，都是因为我们固定了间隔为1，注意间隔和几何间隔的区别）。代入g(x)后的值如果在1和-1之间，我们就拒绝判断。

求这样的g(x)的过程就是求w（一个n维向量）和b（一个实数）两个参数的过程（但实际上只需要求w，求得以后找某些样本点代入就可以求得b）

w不仅跟样本点的位置有关，还跟样本的类别有关（也就是和样本的“标签”有关）。因此用下面这个式子表示才算完整：

w=α₁y₁x₁+α₂y₂x₂+…+α_ny_nx_n

αi是拉格朗日乘数，其中的y_i就是第i个样本的标签，它等于1或者-1。其实以上式子的那一堆拉格朗日乘子中，只有很少的一部分不等于0（不等于0才对w起决定作用），这部分不等于0的拉格朗日乘子后面所乘的样本点，其实都落在H1和H2上，也正是这部分样本（而不需要全部样本）唯一的确定了分类函数

用求和符号简写一下：

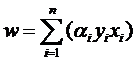
因此原来的g(x)表达式可以写为：

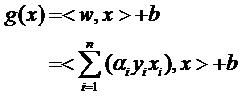
注意式子中x才是变量，也就是你要分类哪篇文档，就把该文档的向量表示代入到 x的位置，而所有的x_i统统都是已知的样本。还注意到式子中只有x_i和x是向量，因此一部分可以从内积符号中拿出来，得到g(x)的式子为：

发现了什么？w不见啦！从求w变成了求α。

求一个线性分类器，它的形式应该是：

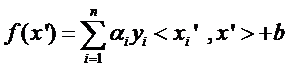
现在这个就是高维空间里的线性函数（为了区别低维和高维空间里的函数和向量，我改了函数的名字，并且给w和x都加上了 ’），我们就可以用一个低维空间里的函数（再一次的，这个低维空间里的函数就不再是线性的啦）来代替，

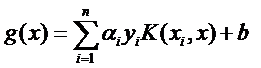
K(w,x)被称作核函数，解决了应用SVM进行非线性分类的问题

我们原先对样本点的要求是：

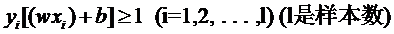
意思是说离分类面最近的样本点函数间隔也要比1大。如果要引入容错性，就给1这个硬性的阈值加一个松弛变量，即允许

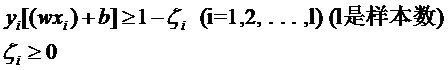
因为松弛变量是非负的，因此最终的结果是要求间隔可以比1小，但是当某些点出现这种间隔比1小的情况时，意味着我们放弃了对这些点的精确分类，而这对我们的分类器来说是种损失。但是放弃这些点也带来了好处，那就是使分类面不必向这些点的方向移动，因而可以得到更大的几何间隔，如何来衡量损失，有两种常用的方式，有人喜欢用

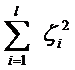
而有人喜欢用

其中l都是样本的数目。两种方法没有大的区别。如果选择了第一种，得到的方法的就叫做二阶软间隔分类器，第二种就叫做一阶软间隔分类器。把损失加入到目标函数里的时候，就需要一个惩罚因子（cost，也就是libSVM的诸多参数中的C），原来的优化问题就变成了下面这样：

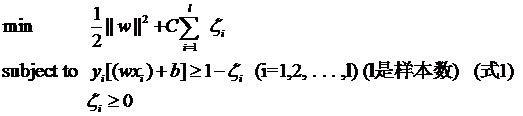
这个式子有这么几点要注意：

一是并非所有的样本点都有一个松弛变量与其对应。实际上只有“离群点”才有，或者也可以这么看，所有没离群的点松弛变量都等于0（对负类来说，离群点就是在前面图中，跑到H2右侧的那些负样本点，对正类来说，就是跑到H1左侧的那些正样本点）。

二是松弛变量的值实际上标示出了对应的点到底离群有多远，值越大，点就越远。

三是惩罚因子C决定了你有多重视离群点带来的损失，显然当所有离群点的松弛变量的和一定时，你定的C越大，对目标函数的损失也越大，此时就暗示着你非常不愿意放弃这些离群点，最极端的情况是你把C定为无限大，这样只要稍有一个点离群，目标函数的值马上变成无限大，马上让问题变成无解，这就退化成了硬间隔问题。

四是惩罚因子C不是一个变量，整个优化问题在解的时候，C是一个你必须事先指定的值，指定这个值以后，解一下，得到一个分类器，然后用测试数据看看结果怎么样，如果不够好，换一个C的值，再解一次优化问题，得到另一个分类器，再看看效果，如此就是一个参数寻优的过程，但这和优化问题本身决不是一回事，优化问题在解的过程中，C一直是定值，要记住。

五是尽管加了松弛变量这么一说，但这个优化问题仍然是一个优化问题。

样本的偏斜问题，也叫数据集偏斜（unbalanced），它指的是参与分类的两个类别（也可以指多个类别）样本数量差异很大。比如说正类有10，000个样本，而负类只给了100个

对付数据集偏斜问题的方法之一就是在惩罚因子上作文章，想必大家也猜到了，那就是给样本数量少的负类更大的惩罚因子，表示我们重视这部分样本，因此我们的目标函数中因松弛变量而损失的部分就变成了：

其中i=1…p都是正样本，j=p+1…p+q都是负样本。libSVM这个算法包在解决偏斜问题的时候用的就是这种方法。

那C₊和C_-怎么确定呢？它们的大小是试出来的（参数调优），但是他们的比例可以有些方法来确定。咱们先假定说C₊是5这么大，那确定C_-的一个很直观的方法就是使用两类样本数的比来算，对应到刚才举的例子，C_-就可以定为500这么大（因为10，000：100=100：1嘛）。

将SVM用于多类分类

一对一方法那样来训练，只是在进行分类之前，我们先按照下面图的样子来组织分类器（如你所见，这是一个有向无环图，因此这种方法也叫做DAG SVM）

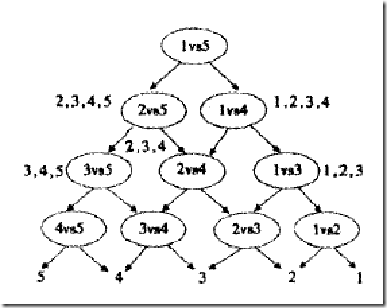
这样在分类时,我们就可以先问分类器“1对5”（意思是它能够回答“是第1类还是第5类”），如果它回答5，我们就往左走，再问“2对5”这个分类器，如果它还说是“5”，我们就继续往左走，这样一直问下去，就可以得到分类结果。

模型出来后，然后通过函数：

输入是x，是一个数组，组中每一个值表示一个特征。输出是A类还是B类。（正类还是负类）

7、
拉格朗日乘数法
（以数学家约瑟夫·拉格朗日命名）

是一种寻找变量受一个或多个条件所限制的多元函数的极值的方法。这种方法将一个有n个变量与k 个约束条件的最优化问题转换为一个有n + k个变量的方程组的极值问题，其变量不受任何约束。这种方法引入了一种新的标量未知数，即拉格朗日乘数：约束方程的梯度（gradient）的线性组合里每个向量的系数。

简单举例：

最大化

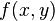
受限于

引入新变量拉格朗日乘数，即可求解下列拉格朗日方程

微积分中最常见的问题之一是求一个函数的极大极小值（极值）。但是很多时候找到极值函数的显式表达是很困难的，特别是当函数有先决条件或约束时。拉格朗日乘数则提供了一个非常便利方法来解决这类问题，而避开显式地引入约束和求解外部变量。

巴特西

数学之路(3)-机器学习(3)-机器学习算法-SVM[5]

最新文章

热门文章