HDU 2993 - MAX Average Problem

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=2993

Consider a simple sequence which only contains positive integers as a1, a2 ... an, and a number k. Define ave(i,j) as the average value of the sub sequence ai ... aj, i<=j. Let’s calculate max(ave(i,j)), 1<=i<=j-k+1<=n.

Input

There multiple test cases in the input, each test case contains two lines.
The first line has two integers, N and k (k<=N<=10^5).
The second line has N integers, a1, a2 ... an. All numbers are ranged in [1, 2000].

Output

For every test case, output one single line contains a real number, which is mentioned in the description, accurate to 0.01.

Sample Input

10 6

6 4 2 10 3 8 5 9 4 1

Sample Output

6.50

题意：

定义ave(i,j) = ( a[i] + a[i+1] + … + a[j-1] + a[j] ) / ( j - i + 1 )，现给定一个整数k且规定j - i + 1 ≥ k，求max(ave(i,j)).

题意：

我们设sum[0~N]是a[1~N]的前n项和，且sum[0]=0，那么就有：

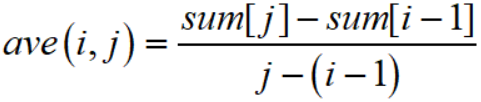
不妨把ave(i,j)看做是点i-1到点j的斜率；

我们设dp[j]代表max(ave(i,j))，j-i+1≥k；

换句话说，在规定最少要连续取到k个值的前提下，a[1~j]中必有一个连续子序列，它以a[j]为结尾，且是所有a[1~j]的连续子序列中平均值最大的，把这个平均值记为dp[j]。

那么题目的最终答案就是max( dp[k] , dp[k+1] , … , dp[N] )。

问题相应可以转化为：

现有0~N这N+1个平面坐标系内的点，每个点P[i]的坐标为(i,sum[i])，0≤i≤N，要求任意横向距离差不小于k的两个点间，最大的斜率为多少。

现在对求斜率有方向化，规定对i<j，只检查从点P[j]到点P[i]的连线的斜率，不检查从P[i]到P[j]的连线。

那么，对于一个点P[j]，定义其检查集合为：

G[j] = {P[i] , 0 ≤ i ≤ j - k }

显然，j取值应当从k到n；当j<k时，G[j]为空集。

那么，dp[j]定义相应可变为：G[j]中任选一个点P[i]，它与P[j]的连线斜率最大，这个斜率记为dp[j]。

那么，在朴素的思想中，我们若要求一个dp[t]，必然要枚举检查G[t]中所有的点；

但是我们通过观察，可以发现如下性质：

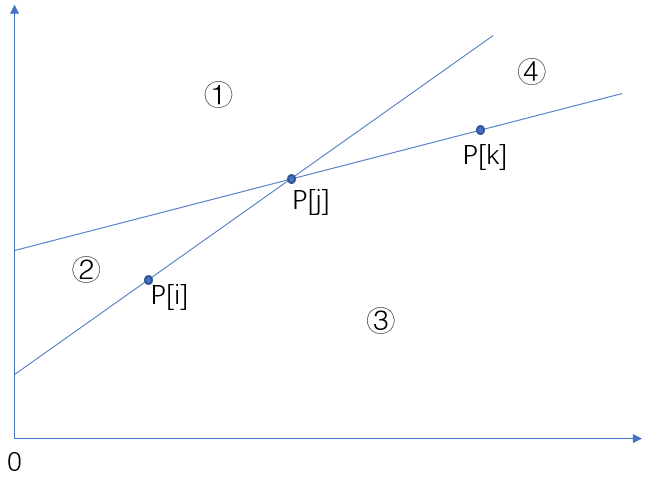
若G[t]中存在三个点P[i],P[j],P[k]，i<j<k，并且P[j]在直线P[i]P[k]的上方，那么必然可以淘汰P[j]。

证明：

设g(P1,P2)代表直线P1P2的斜率，则：

若g(P[j],P[t]) ≥ g(P[i],P[t])，那么P[t]必然落在区域②中；

若g(P[j],P[t]) ≥ g(P[k],P[t])，那么P[t]必然落在区域③中；

但是显然区域②和③显然没有符合条件（t>k）的相交区域，故不可能同时满足g(P[j],P[t]) ≥ g(P[i],P[t])和g(P[j],P[t]) ≥ g(P[k],P[t])；

也就是说要么g(P[j],P[t]) < g(P[i],P[t])，要么g(P[j],P[t]) < g(P[k],P[t])，显然j总归不如i或者k中至少一个优，即证明了j必然淘汰。

这样一来，由于我们去掉了所有上凸的点，就维护了一个下凸的折线图形：

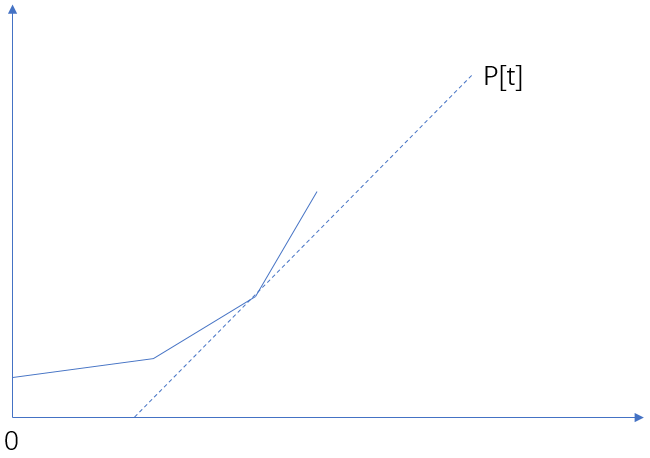
显然当P[t]切到这个折线时，斜率最大，即为dp[t]。

那么相应的我们可以建立一个存储点的队列，维护下凸图形，有以下的算法过程：

　　首先枚举 j = k ~ N，按以下两步尝试计算dp[j]：

　　　　①首先令点i = j - k，尝试将点i入队：

　　　　　　　若队列尾部存在点a和b，且g(a,b) ≥ g(b,i)，则删去元素b；

　　　　　　　（原因：若G[t]中存在三个点P[i],P[j],P[k]，i<j<k，并且P[j]在直线P[i]P[k]的上方，那么必然可以淘汰P[j]。）

　　　　　　　不断重复上述操作，直到队列内元素少于2，或者g(a,b) < g(b,i)；然后将点i入队。

　　　　②现在，所有点P[0]到点P[j - k]都曾经进入过队列了，那么此时可以通过队列的性质计算dp[j]：

　　　　　　　若队列头部存在点a和b，且g(a,b) ≤ ave(b,j)，则将元素a删去；

　　　　　　　反复上述操作，直到队列元素少于2，或者ave(a,b) > ave(b,j)；然后再选取队头元素得到dp[j]=g(q[head],j)。

　　　　　　　这样做的原因上面讲过，不再赘述。

　　　　　　　（删去的这些队列头部的元素，不难发现，在求dp[j]时它们不能成为最优解，在往后的dp[j+1],dp[j+2]……中依然不可能成为最优解，所以可以直接删去。）

AC代码：

#include<bits/stdc++.h>

using namespace std;

const int maxn=1e5+;

int n,k,sum[maxn];

int q[maxn],head,tail;

//输入外挂

int tot;

const int BUF=;

char Buf[BUF],*buf=Buf;

inline void read(int &a)

{

    for(a=;*buf<;buf++);

    while(*buf>) a=a*+*buf++-;

}

double inline g(int i,int j){return (double(sum[j]-sum[i]))/(double(j-i));}

int main()

{

    tot=fread(Buf,,BUF,stdin);

    while()

    {

        if(buf-Buf+>=tot) break;

        read(n),read(k);

        sum[]=;

        for(int i=;i<=n;i++)

        {

            read(sum[i]);

            sum[i]+=sum[i-];

        }

        head=tail=;

        double ans=;

        for(int j=k;j<=n;j++)

        {

            int i=j-k;

            while( head+<tail && g(q[tail-],q[tail-])>=g(q[tail-],i) ) tail--;

            q[tail++]=i;

            while( head+<tail && g(q[head],q[head+])<=g(q[head+],j) ) head++;

            ans=max(ans,g(q[head],j));

        }

        printf("%.2f\n",ans);

      }

}

注意点：

①要使用输入加速外挂，而且不能是一般的getchar版的，要是fread版的加速挂。

②结合前一道题目http://www.cnblogs.com/dilthey/p/8745843.html来看，斜率DP一定要讲究理论基础，理论严密基础扎实，写出来的代码才不会WA。

巴特西

HDU 2993 - MAX Average Problem - [斜率DP]

最新文章

热门文章