Sigma Function （LightOJ - 1336）【简单数论】【算术基本定理】【思维】

标签：入门讲座题解数论

题目描述

Sigma function is an interesting function in Number Theory. It is denoted by the Greek letter Sigma (σ). This function actually denotes the sum of all divisors of a number. For example σ(24) = 1+2+3+4+6+8+12+24=60. Sigma of small numbers is easy to find but for large numbers it is very difficult to find in a straight forward way. But mathematicians have discovered a formula to find sigma. If the prime power decomposition of an integer is

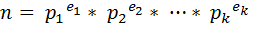
Then we can write,

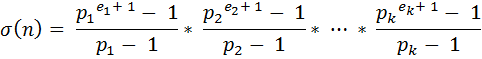
For some n the value of σ(n) is odd and for others it is even. Given a value n, you will have to find how many integers from 1 to n have even value of σ.

Input

Input starts with an integer T (≤ 100), denoting the number of test cases.

Each case starts with a line containing an integer n (1 ≤ n ≤ 1012).

Output

For each case, print the case number and the result.

Sample Input

Sample Output

Case 1: 1

Case 2: 5

Case 3: 83

Case 4: 947

题意

约数和函数$$\sigma{(n)} = \sum_{d | n} d;.$$

给定$n$，询问$[1, n]$区间内有几个$i$，使得$\sigma{(i)}$为偶数？

解析

根据算数基本定理，正整数$n$，有唯一质因数分解形式，$$n = p_1^{\alpha_1}\cdot p_2^{\alpha_2} \cdot p_3^{\alpha_3} \cdot ,,\cdots ,, \cdot p_n^{\alpha_n}\quad(p_i ;is ;a ;prime).$$

那么，根据乘法计数原理，显然有$\sigma{(n)} = (1 + p_1^1 + p_1^2 + \cdots p_1^{\alpha_1}) \cdot (1 + p_2^1 + p_2^2 + \cdots + p_2^{\alpha_2}) \cdot (1 + p_3^1 + p_3^2 + \cdots + p_3^{\alpha_3}) \cdot \,\, \cdots \,\, \cdot (1 + p_n^1 + p_n^2 + \cdots + p_n^{\alpha_n})$.

正难则反，我们不方便研究$\sigma{(n)}$为偶数的情况，我们可以研究$\sigma{(n)}$为奇数的个数，然后用总数减掉奇数个数，就得到偶数个数。

首先，我们要清楚

偶数 + 偶数 = 偶数

奇数 + 偶数 = 奇数

奇数 + 奇数 = 偶数
偶数 * 偶数 = 偶数

奇数 * 偶数 = 偶数

奇数 * 奇数 = 奇数。

我们知道，只有让$\sigma{(n)}$的全部因数都为奇数才可以使$\sigma{(n)}$为奇数。

若$2 \,| \,n$，则$(1 + p_1^1 + p_1^2 + \cdots p_1^{\alpha_1})$这项一定是奇数。因为$2$的任何次幂都是偶数，且偶数 + 奇数 = 奇数。
对于除$2$以外的其他质数，它的任何次幂都一定是奇数。要想使因数项为奇数，则只能构造($1 + $ 偶数) 的这种形式.当有偶数个奇数相加时，它们的和是偶数。所以，$\alpha_1,\alpha_2, \alpha_3, \dots,\alpha_n$（不包括$2$的指数）都应该是偶数。
$n$ 可以是一个完全平方数。当$n$是一个完全平方数时，$\alpha_1,\alpha_2, \alpha_3, \dots,\alpha_n$都是偶数。因为$n$可以找到两个完全相同的因子。

或者，$n$可以是$2 \times $ 完全平方数。因为把$2$当作底数的因数项永远是奇数，所以乘上$2$依然能保持所有乘数项都是奇数。（为什么没有$2^2, 2^3, 2^4, \dots \times $ 完全平方数？当$2$的指数为偶数时，用完全平方数就可以找到这个数。如果是奇数时，指数 = 1 + 偶数，又还原为$2 \times $ 完全平方数。）
综上，$ans = n - \sqrt{n} - \sqrt{n / 2}$。

通过代码

/*

Problem

    LightOJ - 1336

Status

	Accepted

Time

	151ms

Memory

	2084kB

Length

	411

Lang

	C++

Submitted

	2019-11-26 23:30:58

RemoteRunId

	1641328

*/

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;

int main()

{

    int times, kase = 0;

    scanf("%d", &times);

    while(times --){

        ll n, cnt = 0;                //cnt也有可能会超过1e9，所以要声明为long long类型.

        scanf("%lld", &n);

        for(ll i = 1; i * i <= n; i ++){

            cnt ++;                 //不超过n的完全平方数计数.

            if(2 * i * i <= n)

                cnt ++;             //不超过n/2的完全平方数计数.

        }

        printf("Case %d: %lld\n", ++ kase, n - cnt);

    }

    return 0;

}

巴特西

Sigma Function （LightOJ - 1336）【简单数论】【算术基本定理】【思维】

Sigma Function （LightOJ - 1336）【简单数论】【算术基本定理】【思维】

题目描述

题意

解析

通过代码

最新文章

热门文章