图——图的Prim法最小生成树实现

1，运营商的挑战：

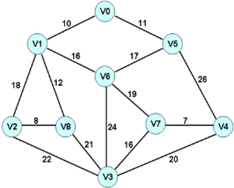
1，在下图标出的城市间架设一条通信线路；

2，要求：

1，任意两个城市间都能够通信；

2，将架设成本降至最低；

2，问题抽象：

1，如何在图中选择 n - 1 条边使得 n 个顶点间两两可达，并且这 n - 1 条边的权值之和最小？

3，最小（大）生成树：

1，仅使用图中的 n - 1 条边连接图中的 n 个顶点；

2，不能使用产生回路的边；

3，各边上的权值总和达到最小（大）；

4，寻找最小生成树：

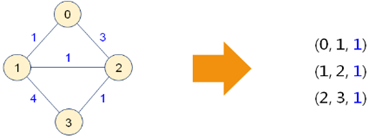
5，使用 prim 方法手工寻找最小生成树：

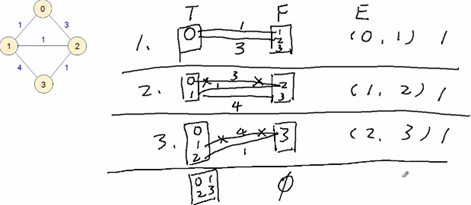
6，最小生成树算法步骤（prim）：

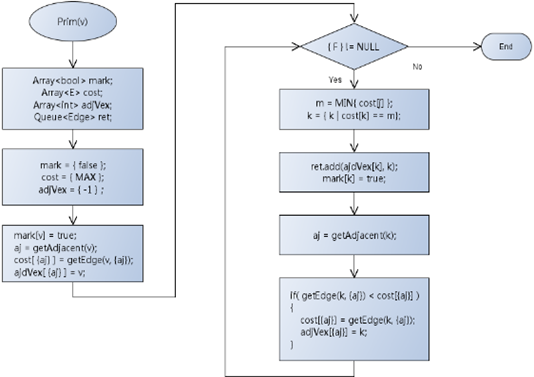
1，选择某一顶点 v0 作为起始顶点，使得 T = {v0}，F = {v1, v2, ..., vn}，E = {}；

2，每次选择一条边，这条边是所有（u, v）中权值最小的边，且 u 属于 T，v 属于 F；

3，修改 T，F，E：

T = T + {v}, F = F - {v}, E = E + {(u, v)}

4，当 F != NULL 时，且（u, v）存在，转 2；否则，结束；

7，最小生成树算法的原材料：

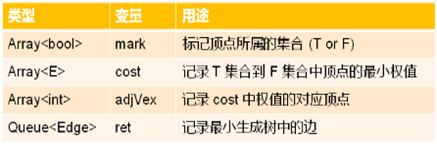
1，如果 T 集合到 F 集合中同一个顶点的连接有多条，那么选取权值最小的连接；

8，最小生成树算法流程图：

9，注意事项：

1，最小生成树仅针对无向图有意义；

2，必须判断图对象是否能够看做无向图；

1，如果可以才能够用 prim 算法；

10，有向图可看做无向图的充分条件：

1，有向的任意两顶点之间若存在连接，则两顶点相互可达、权值相等；

11，图类型（Graph）中的新增成员函数：

1，virtual bool isAdjacent(int i, int j) = 0；

1，判断在当前图中顶点 i 到顶点 j 是否邻接；

2，bool asUndirected()；

1，判断当前的有向图是否能够看做无向图；

12，最小生成树 prim 算法实现：

　1，判断邻接的实现：
　　1，邻接矩阵的实现：

     /* 判断 i 到 j 顶点边是否连接，值不为空就连接 */

     bool isAdjacent(int i, int j)

     {

         return ( <= i) && (i < vCount()) && ( <= j) && (j < vCount()) && (m_edges[i][j] != NULL);

     }

　　2，邻接链表的实现：

     bool isAdjacent(int i, int j)

     {

         return ( <= i) && (i < vCount()) && ( <= j) && (j < vCount()) && (m_list.get(i)->edge.find(Edge<E>(i, j)) >= );

     }

　 2，判断是否为无向图的实现：

 　　 /* 最小生成树只能用于无向图，而我们针对的是有向图，所以要判断有向图什么时候能够被当做无向图 */

     bool asUndirected()

     {

        bool ret = true;

        for(int i=; i<vCount(); i++)

        {

            for(int j=; j<vCount(); j++)

            {

                /* i 到 j 是连接的，并且 j 到 i 也是连接的，然后权值也要相等 */

                if( isAdjacent(i, j) )

                {

                    ret = ret && isAdjacent(j, i)  && (getEdge(i, j) == getEdge(j, i));

                }

            }

        }

        return ret;

     }

　　3，Prim算法实现：

 　　 /* Prim 法实现最小、大生成树；返回值是数组，因为最小、大生成树的结果就是一系列的边，所以返回边的数组；参数表示理论上的最大权值； */

     SharedPointer< Array< Edge<E> > > prim(const E& LIMIT, const bool MINIMUM = true)  // 返回一个指向存储边的数组指针

     {

         LinkQueue< Edge<E> > ret;  // 返回边队列，本质是 E 集合

         /* 执行 prim 算法 */

         if( asUndirected() )  // 无向图

         {

             DynamicArray<int> adjVex(vCount());//保存最小权值的边的 F集合中顶点

             DynamicArray<bool> mark(vCount());  // 保存 T 集合或者 F 集合的标记

             DynamicArray<E> cost(vCount());  // 保存最小权值的顶点中 E 集合中顶点，寻找最小值要配合 mark 使用

             SharedPointer< Array<int> > aj = NULL;  // 保存某个顶点邻接数组

             bool end = false;  // 用于标记判断 prim 是否要中断执行

             int v = ;  // 代表习惯性的从 0 顶点生成最小生成树

             /* 执行初始化 */

             for(int i=; i<vCount(); i++)

             {

                 adjVex[i] = -;  // 没有边被访问

                 mark[i] = false;  // 顶点都没有被访问

                 cost[i] = LIMIT;  // 参数传递理论上的最大权值

             }

             mark[v] = true;  // 初始顶点做标记

             aj = getAdgacent(v);  // 获取初始顶点的邻接顶点

             /* 设置初始顶点对应的位置 */

             for(int j=; j<aj->length(); j++)

             {

                 cost[(*aj)[j]] = getEdge(v, (*aj)[j]);  // 保存/到对应顶点的响应权值

                 adjVex[(*aj)[j]] = v;  // 记录权值所对应的顶点，即能够得到边

             }

             /* 真正循环找边 */

             for(int i=; (i<vCount()) && !end; i++)  // 最多循环顶点次；也可能条件不满足，提前结束，所以有 !end

             {

                 E m = LIMIT;

                 int k = -;  // 记录最小值的顶点

                 /* 通过 cost 数组找最小值 */

                 for(int j=; j<vCount(); j++)

                 {

                     if( !mark[j] && (MINIMUM ? (cost[j] < m) : (cost[j] > m)) ) // !makr[j] 条件是因为选取最小权值时本质上是选取连接的最小边，对应的顶点是在 F集合，此时 mark 中对应的值为假当中的，则在 mark 数组中对应的就为假，所以要这个条件，这里有最小值最大值的设置

           {

                         m = cost[j];

                         k = j;  // 得到记录的最小值的顶点号

                     }

                 }

                 end = (k == -);  // 是否找到合法最小权值，因为有可能在上面 if 条件中没有找到合法的最小权值

                 if( !end )

                 {

                     ret.add(Edge<E>(adjVex[k], k, getEdge(adjVex[k], k)));  // 在 adjVex 中找到这条边

                     mark[k] = true;  // 标记顶点进入了 T 集合

                     aj = getAdgacent(k);  // 找新的集合连接

                     /* 找到之后更新 cost 数组和 adgVex 数组 */

                     for(int j=; j<aj->length(); j++)

                     {

                         if( !mark[(*aj)[j]] && (MINIMUM ? (getEdge(k, (*aj)[j]) < cost[(*aj)[j]]) : (getEdge(k, (*aj)[j]) > cost[(*aj)[j]])) );  //只对 F 集合操作

                         {

                             cost[(*aj)[j]] = getEdge(k ,(*aj)[j]); //如果 T 到 F 集合新连接权值较小，则记录到 cost 数组中,新加入的点 k 和之前 T 集合里的点到 F 集合里的点的权值要比较呢；如果在 k 到 F 集合中找不到合适的点，则用T中的点代替

                             adjVex[(*aj)[j]] = k;  // 将最小权值的起始点设入到邻接边中

                         }

                     }

                 }

             }

         }

         else

         {

             THROW_EXCEPTION(InvalidOperationException, "Prim operation is for undirected graph only ...");

         }

         /* 判断边的数目是否够，即 n-1 条边 */

         if( ret.length() != (vCount() - ) )

         {

             THROW_EXCEPTION(InvalidOperationException, "No enough edge for prim operation ...");

         }

         return toArray(ret);  // 返回值是边的数组

     }

14，prim 算法测试代码：

 #include <iostream>

 #include "MatrixGraph.h"

 #include "ListGraph.h"

 using namespace std;

 using namespace DTLib;

 template< typename V, typename E >

 Graph<V, E>& GraphEasy()

 {

 　　 static MatrixGraph<, V, E> g;

     g.setEdge(, , );

     g.setEdge(, , );

     g.setEdge(, , );

     g.setEdge(, , );

     g.setEdge(, , );

     g.setEdge(, , );

     g.setEdge(, , );

     g.setEdge(, , );

     g.setEdge(, , );

 　　 g.setEdge(, , );

     return g;

 }

 template< typename V, typename E >

 Graph<V, E>& GraphComplex()

 {

 　　 static ListGraph<V, E> g();

     g.setEdge(, , );

     g.setEdge(, , );

     g.setEdge(, , );

     g.setEdge(, , );

     g.setEdge(, , );

     g.setEdge(, , );

     g.setEdge(, , );

     g.setEdge(, , );

     g.setEdge(, , );

     g.setEdge(, , );

     g.setEdge(, , );

     g.setEdge(, , );

     g.setEdge(, , );

     g.setEdge(, , );

     g.setEdge(, , );

     g.setEdge(, , );

     g.setEdge(, , );

     g.setEdge(, , );

     g.setEdge(, , );

     g.setEdge(, , );

     g.setEdge(, , );

     g.setEdge(, , );

     g.setEdge(, , );

     g.setEdge(, , );

     g.setEdge(, , );

     g.setEdge(, , );

     g.setEdge(, , );

     g.setEdge(, , );

     g.setEdge(, , );

 　　 g.setEdge(, , );

     return g;

 }

 int main()

 {

     Graph<int, int>& g = GraphEasy<int, int>();

 　　 SharedPointer< Array< Edge<int> > > sa = g.prim();  

 　　 int w = ;

     for(int i=; i<sa->length(); i++)

     {

         w += (*sa)[i].data;

         cout << (*sa)[i].b << " " << (*sa)[i].e << " " << (*sa)[i].data << endl;

 　　 }

 　　 cout << "Weight: " << w << endl;

     return ;

 }

15，小结：

1，最小生成树使得顶点间的连通代价最小；

2，Prim 算法通过顶点的动态标记寻找最小生成树；

3，Prim 算法的关键是集合概念的运用（T 集合，F 集合）；

4，利用 Prim 算法的思想也能寻找图的“最大生成树”；

巴特西

图——图的Prim法最小生成树实现

最新文章

热门文章