强化学习（六）：n-step Bootstrapping

n-step Bootstrapping

n-step 方法将Monte Carlo 与 one-step TD统一起来。 n-step 方法作为 eligibility traces 的引入，eligibility traces 可以同时的在很多时间间隔进行bootstrapping.

n-step TD Prediction

one-step TD 方法只是基于下一步的奖励，通过下一步状态的价值进行bootstrapping，而MC方法则是基于某个episode的整个奖励序列。n-step 方法则是基于两者之间。使用n 步更新的方法被称作n-step TD 方法。

对于MC方法，估计\(v_{\pi}(S_t)\)，使用的是完全收益(complete return)是：

\[G_t \dot = R_{t+1} +\gamma R_{t+2}+ \gamma^2R_{t+3}+...+\gamma^{T-t-1}R_T
\]

而在one-step TD方法中，则是一步收益(one-step return)：

\[G_{t:t+1}\dot = R_{t+1} +\gamma V(S_{t+1})
\]

那么n-step return：

\[G_{t:t+n} \dot = R_{t+1} + \gamma R_{t+2} + ...+\gamma^{n-1} R_{t+n} + \gamma^{n} V_{t+n-1}(S_{t+n})
\]

其中 \(n\ge 1, 0\le t< T-n\)。

因为在t+n 时刻才可知道 \(R_{t+n}, V_{t+n-1}\) ,故可定义：

\[V_{t+n}(S_t)\dot = V_{t+n-1}(S_t) + \alpha[ G_{t:t+n} - V_{t+n-1}(S_t)]
\]

# n-step TD for estimating V = v_pi

Input: a policy pi

Algorithm parameters: step size alpha in (0,1], a positive integer n

Initialize V(s) arbitrarily, s in S

All store and access operations (for S_t and R_t) can take their index mod n+1

Loop for each episode:

     Initialize and store S_0 != terminal

     T = infty

     Loop for t = 0,1,2,...

         if t < T, then:

             Take an action according to pi(.|S_t)

             Observe and store the next reward as R_{t+1} and the next state as S_{t+1}

             If S_{t+1} is terminal, then T = t + 1

         tau = t - n + 1 (tau is the time whose state's estimate is being updated)

         if tau >= 0:

             G = sum_{i = tau +1}^{min(tau+n,T)} gamma^{i-tau-1} R_i

             if tau + n < T, then G = G + gamma^n V(S_{tau+n})

             V(S_{tau}) = V(S_{tau} + alpha [G - V(S_tau)])

     Until tau = T - 1

n-step Sarsa

与n-step TD方法类似，只不过n-step Sarsa 使用的state-action对，而不是state：

\[G_{t:t+n} \dot = R_{t+1} + \gamma R_{t+2} + ...+\gamma^{n-1} R_{t+n} + \gamma^{n} Q_{t+n-1}(S_{t+n}，A_{t+n}) \qquad n\ge1, 0 \le t \le T-n
\]

自然地：

\[Q_{t+n}(S_t,A_t) \dot = Q_{t+n-1}(S_t,A_t) + \alpha[G_{t:t+n} - Q_{t+n-1}(S_t,A_t)]\qquad 0\le t< T
\]

# n-step Sarsa for estimating Q = q* or q_pi

Initialize Q(s,a) arbitrarily, for all s in S, a in A

Initialize pi to be e-greedy with respect to Q, or to a fixed given policy

Algorithm parameters: step size alpha in (0,1], small e >0, a positive integer n

All store and access operations (for S_t, A_t and R_t) can take their index mod n+1

Loop for each episode:

     Initialize and store S_o != terminal

     Select and store an action A_o from pi(.|S_0)

     T = infty

     Loop for t = 0,1,2,...:

         if t < T, then:

             Take action A_t

             Observe and store the next reward as R_{t+1} and the next state as S_{t+1}

             If S_{t+1} is terminal, then:

                  T = t + 1

             else:

                 Select and store an action A_{t+1} from pi(.|S_{t+1})

         tau = t - n + 1 (tau is the time whose estimate is being  updated)

         if tau >= 0:

             G = sum_{i = tau+1}^{min(tau+n,T)} gamma^{i-tau-1}R_i

             if tau + n < T, then G = G + gamma^nQ(S_{tau +n}, A_{tau+n})

             Q(S_tau,A_tau) = Q(S_{tau},A_{tau}) + alpha [ G - Q(S_{tau},A_{tau})]

至于 Expected Sarsa：

\[G_{t:t+n}\dot = R_{t+1} +... + \gamma^{n-1}R_{t+n} + \gamma^n \bar V(t+n-1) (S_{t+n}), \qquad t+n < T
\]

\[\bar V_t(s) \dot = \sum_{a}\pi(a|s)Q_t(s,a),\qquad \forall s\in S.
\]

n-step Off-policy Learning by Importance Sampling

一个简单off-policy 版的 n-step TD:

\[V_{t+n}(S_t) = \dot = V_{t+n -1}(S_t) + \alpha \rho_{t:t+n-1}[G_{t:t+n} - V_{t+n -1}(S_t)], 0 \le t < T
\]

其中 \(\rho_{t:t+n-1}\) 是 importance sampling ratio：

\[\rho_{t:h} \dot = \Pi_{k =t}^{min(h, T -1)} \frac{\pi(A_k|S_k)}{b(A_k|S_k)}
\]

off-policy n-step Sarsa更新形式：

\[Q_{t+n}(S_t, A_t) \dot = Q_{t+n -1}( S_t, A_t) + \alpha \rho_{t+1:t+n} [ G_{t:t+n} - Q_{t+n-1} (S_t, A_t)]
\]

# Off-policy n-step Sarsa for estimating Q = q* or q_pi

Input: an arbitrary behavior policy b such that b(a|s) > 0, for all s in S, a in A

Initialize pi to be greedy with respect to Q, or as a fixed given policy

Algorithm parameters: step size alpha in (0,1], a positive integer n

All store and access operations (for S_t, A_t, and R_t) can take their index mod n + 1

Loop for each episode:

    Initialize and store S_0 != terminal

    Select and store an action A_0 from b(.|S0)

    T = infty

    Loop for t = 0,1,2,...:

        if t<T, then:

            take action At

            Observe and store the next reward as R_{t+1} and the next state as S_{t+1}

            if S_{t+1} is terminal, then:

                 T = t+1

            else:

                 select and store an action A_{t+1} from b(.|S_{t+1})

        tau = t - n + 1 (tau is the time whose estimate is being updated)

        if tau >=0:

            rho = \pi_{i = tau+1}^min(tau+n-1, T-1) pi(A_i|S_i)/b(A_i|S_i)

            G = sum_{i = tau +1}^min(tau+n, T) gamma^{i-tau-1}R_i

            if tau + n < T, then: G = G + gamma^n Q(S_{tau+n}, A_{tau+n})

            Q(S_tau,A_tau) = Q(S_tau, A_tau) + alpha rho [G-Q(s_tau, A_tau)]

            if pi is being learned, then ensure that pi(.|S_tau) is greedy wrt Q

    Until tau = T - 1

Per-decision Off-policy Methods with Control Variates

pass

Off-policy Learning without Importance Sampling: The n-step Tree Backup Algorithm

tree-backup 算法是一种可以不借助importance sampling的off-policy n-step 方法。 tree-backup 的更新基于整个估计行动价值树，或者说，更新是基于树中叶结点（未被选中的行动）的估计的行动价值。树的内部的行动结点（即实际被选择的行动）不参加更新。

\[G_{t:t+1} \dot = R_{t+1} + \gamma\sum_{a}\pi(a|S_{t+1})Q_t(S_{t+1},a)
\]

\[\begin{array}\\
G_{t:t+2} &\dot =& R_{t+1} + \gamma\sum_{a \ne A_{t+1}} \pi(a|S_{t+1})Q_{t+1}(S_{t+1},a)+ \gamma \pi(A_{t+1}|S_{t+1})(R_{t+2}+\gamma \sum_{a}\pi(a|S_{t+2},a)) \\
& = & R_{t+1} + \gamma\sum_{a\ne A_{t+1}}\pi(a|S_{t+1})Q_{t+1}(S_{t+1},a) + \gamma\pi(A_{t+1}|S_{t+1})G_{t+1:t+2}
\end{array}
\]

于是

\[G_{t:t+n} \dot = R_{t+1} + \gamma\sum_{a\ne A_{t+1}}\pi(a|S_{t+1})Q_{t+1}(S_{t+1},a) + \gamma\pi(A_{t+1}|S_{t+1})G_{t+1:t+n}
\]

算法更新规则：

\[Q_{t+n}(S_t,A_t)\dot = Q_{t+n-1}(S_t, A_t) + \alpha [ G_{t:t+n} - Q_{t+n -1}(S_t,A_t)]
\]

# n-step Tree Backup for estimating Q = q* or q_pi

Initialize Q(s,a) arbitrarily, for all s in S, a in A

Initialize pi to be greedy with respect to Q, or as a fixed given policy

Algorithm parameters: step size alpha in (0,1], a positive integer n

All store and access operations can take their index mod n+1

Loop for each episode:

    Initialize and store S_0 != terminal

    Choose an action A_0 arbitrarily as a function of S_0; Store A_0

    T = infty

    Loop for t = 0,1,2,...:

        If t < T:

            Take action A_t; observe and store the next reward and state as R_{t+1}, S_{t+1}

            if S_{t+1} is terminal:

                T = t + 1

            else:

                Choose an action A_{t+1} arbitrarily as a function of S_{t+1}; Store A_{t+1}

        tau = t+1 - n (tau is the time whose estimate is being updated)

        if tau >= 0:

            if t + 1 >= T:

                G = R_T

            else:

                G = R_{t+1} + gamma sum_{a} pi(a|S_{t+1})Q(S_{t+1},a)

            Loop for k = min(t, T - 1) down through tau + 1:

                G = R_k + gamma sum_{a != A_k}pi(a|S_k)Q(S_k,a) + gamma pi(A_k|S_k) G

            Q(S_tau,A_tau) = Q(S_tau,A_tau) + alpha [G - Q(S_tau,A_tau)]

            if pi is being learned, then ensure that pi(.|S_tau) is greedy wrt Q

     Until tau = T - 1

*A Unifying Algorithm: n-step Q(\(\sigma\))

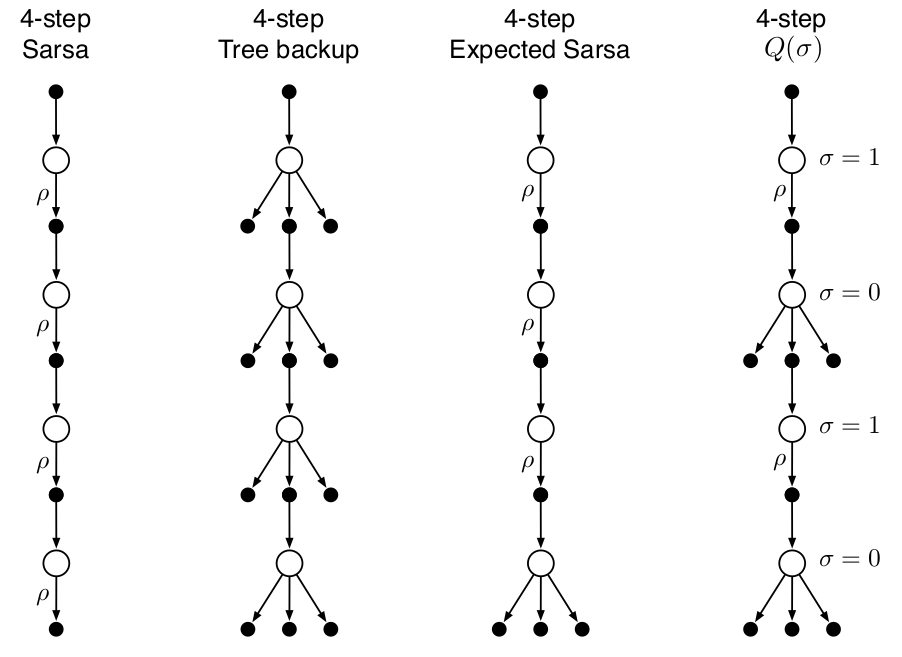
在n-step Sarsa方法中，使用所有抽样转换(transitions),　在tree-backup 方法中，使用state-to-action所有分支的转换，而非抽样，而在期望 n-step 方法中，除了最后一步不使用抽样而使用所有分支的转换外，其他所有都进行抽样转换。

为统一以上三种算法，有一种思路是引入一个随机变量抽样率:\(\sigma\in [0,1]\)，当其取１时，表示完全抽样，当取０时表示使用期望而不抽样。

根据tree-backup n-step return (h = t + n)以及\(\bar V\)：

\[\begin{array}\\
G_{t:h} &\dot =& R_{t+1} + \gamma\sum_{a\ne A_{t+1}}\pi(a|S_{t+1})Q_{t+1}(S_{t+1},a) + \gamma\pi(A_{t+1}|S_{t+1})G_{t+1:h}\\
& = & R_{t+1} +\gamma \bar V_{h-1} (S_{t+1}) - \gamma\pi(A_{t+1}|S_{t+1})Q_{h-1}(S_{t+1},A_{t+1}) + \gamma\pi(A_{t+1}| S_{t+1})G_{t+1:h}\\
& =& R_{t+1} +\gamma\pi(A_{t+1}|S_{t+1})(G_{t+1:h} - Q_{h-1}(S_{t+1},A_{t+1})) + \gamma \bar V_{h-1}(S_{t+1})\\
\\
&& (\text{引入},　\sigma)\\
\\
& = & R_{t+1} + \gamma(\sigma_{t+1}\rho_{t+1} + (1 - \sigma_{t+1})\pi(A_{t+1}|S_{t+1}))(G_{t+1:h} - Q_{h-1}(S_{t+1}, A_{t+1})) + \gamma \bar V_{h-1}(S_{t+1})
\end{array}
\]

# n-step Tree Backup for estimating Q = q* or q_pi

Initialize Q(s,a) arbitrarily, for all s in S, a in A

Initialize pi to be greedy with respect to Q, or as a fixed given policy

Algorithm parameters: step size alpha in (0,1], a positive integer n

All store and access operations can take their index mod n+1

Loop for each episode:

    Initialize and store S_0 != terminal

    Choose an action A_0 arbitrarily as a function of S_0; Store A_0

    T = infty

    Loop for t = 0,1,2,...:

        If t < T:

            Take action A_t; observe and store the next reward and state as R_{t+1}, S_{t+1}

            if S_{t+1} is terminal:

                T = t + 1

            else:

                Choose an action A_{t+1} arbitrarily as a function of S_{t+1}; Store A_{t+1}

                Select and store sigma_{t+1}

                Store rho_{t+1} = pi(A_{t+1}|S_{t+1})/b(A_{t+1}|S_{t+1})

        tau = t+1 - n (tau is the time whose estimate is being updated)

        if tau >= 0:

            G = 0

            Loop for k = min(t, T - 1) down through tau + 1:

                if k = T:

                    G = R_t

                else:

                     V_bar = sum_{a} pi(a|S_k) Q(S_k,a)

                     G = R_k + gamma(simga_k rho_k + (1-simga_k)pi(A_k|S_k))(G - Q(S_k,A_k)) + gamma V_bar

            Q(S_tau,A_tau) = Q(S_tau,A_tau) + alpha [G - Q(S_tau,A_tau)]

            if pi is being learned, then ensure that pi(.|S_tau) is greedy wrt Q

     Until tau = T - 1

巴特西