Solution -「LOCAL」大括号树
2024-10-19 23:38:06
\(\mathcal{Description}\)
OurTeam & OurOJ.
给定一棵 \(n\) 个顶点的树，每个顶点标有字符 ( 或 )。将从 \(u\) 到 \(v\) 的简单有向路径上的字符串成括号序列，记其正则匹配的子串个数为 \(\operatorname{ans}(u,v)\)。求：
\[\sum_{u=1}^n\sum_{v=1}^n\operatorname{ans}(u,v)\bmod998244353
\]
\]
\(n\le2\times10^5\)。
\(\mathcal{Solution}\)
可以先回忆一下括号树嗷。
来看看链怎么做 owo，现有结点按 \(1\sim n\) 从左到右编号，记 \(s(i,j)\) 表示从 \(i\) 到 \(j\) 串成的括号序列。令 \(\operatorname{match}(i)\) 为最大的 \(j<i\)，满足 \(s(j,i)\) 正则匹配。定义状态 \(f(i)\) 表示 \(s(1,i)\) 中，以 \(i\) 结尾的正则子串贡献。那么：
\[f(i)=f(\operatorname{match}(i)-1)+\operatorname{match}(i)
\]
\]
即，先保证最短的以 \(i\) 结尾的正则，起点就可以在前面任选了。而事实上，终点也能任选，那么答案为：
\[\sum_{i=1}^nf(i)(n-i+1)
\]
\]
需要正反分别做一次嗷。
那么，搬到树上，一个正则会贡献多少次呢？如图（混V的请告诉我背景是谁吖~）：
不难发现，\((u,v)\)（或 \((v,u)\)）若正则匹配，则它对答案的贡献为 \(siz_u\times siz_v\)。
好啦，开始 \(\text{DSU on Tree}\) 吧！
注意到我们只关心一些子树大小的信息，所以这样设计状态：
- \(f(u,i)\) 表示 \(u\) 子树内某一点 \(v\) 到 \(u\)，构成的串有 \(i\) 个
(失配，且所有)被匹配的 \(siz_v\) 之和。 - \(g(u,i)\) 表示 \(u\) 到其子树内某一点 \(v\)，构成的串有 \(i\) 个
)失配，且所有(被匹配的 \(siz_v\) 之和。
好奇怪的定义 qwq，该怎样理解呢？
考虑一条 \(v-u-w\) 的有向树链，其中 \(u\) 是 \(v\) 与 \(w\) 的 \(\text{LCA}\)。若 \(v-u\) 长成 (...((...(，\(u-w\) 长成 ...)...)...))，其中 ... 是已匹配的括号。可见 \(v-u-w\) 是正则匹配的，而这正对应了我们的状态 \(f(u,4)\) 和 \(g(u,4)\)！
接着考虑轻重儿子信息对答案的贡献，如图：
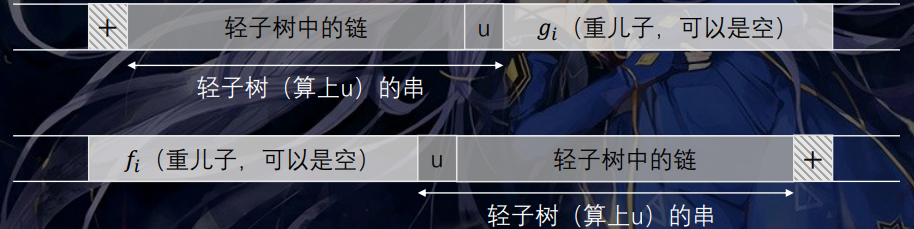
\(\text{DFS}\) 轻儿子的时候，用线段树动态维护前缀的 )，后缀的 ( 是否出现失配的情况，若一个点加入后不存在失配，则用 DP 信息更新答案。合并信息时类似，但加入最后一个点 \(u\) 时：
\(s_u=\texttt{'('}\)，\(f(u,i+1)=f(v,i)\)，\(g(u,i-1)=f(v,i)\)。
\(s_u=\texttt{')'}\)，\(f(u,i-1)=f(v,i)\)，\(g(u,i+1)=f(v,i)\)。
这……总不可能 \(\mathcal O(siz)\) 地遍历第二维吧 qwq。事实上，发现这只是一个单纯的数组位移，初始时开两倍数组，用一个指针指向数组实际的 \(0\) 号为即可 \(\mathcal O(1)\) 实现了。
以上两幅配图来自 Lucky_Glass 的题解。
\(\mathcal{Code}\)
#include <cstdio>
const int MAXN = 2e5, MOD = 998244353;
int n, ecnt, head[MAXN + 5], siz[MAXN + 5], son[MAXN + 5];
int ans, aryf[MAXN * 2 + 5], aryg[MAXN * 2 + 5], *f, *g;
char s[MAXN + 5];
inline int add ( int a, const int b ) { return ( a += b ) < MOD ? a : a - MOD; }
inline int sub ( int a, const int b ) { return ( a -= b ) < 0 ? a + MOD : a; }
inline int mul ( long long a, const int b ) { return ( a *= b ) < MOD ? a : a % MOD; }
inline int rint () {
int x = 0; char s = getchar ();
for ( ; s < '0' || '9' < s; s = getchar () );
for ( ; '0' <= s && s <= '9'; s = getchar () ) x = x * 10 + ( s ^ '0' );
return x;
}
struct Edge { int to, nxt; } graph[MAXN + 5];
inline void link ( const int s, const int t ) {
graph[++ ecnt] = { t, head[s] };
head[s] = ecnt;
}
struct SegmentTree {
int mn[MAXN * 2 + 5], tag[MAXN * 2 + 5];
inline int id ( const int l, const int r ) { return ( l + r ) | ( l != r ); }
inline void pushad ( const int l, const int r, const int v ) {
int rt = id ( l, r );
mn[rt] += v, tag[rt] += v;
}
inline void pushdn ( const int l, const int r ) {
int rt = id ( l, r ), mid = l + r >> 1;
if ( ! tag[rt] ) return ;
pushad ( l, mid, tag[rt] ), pushad ( mid + 1, r, tag[rt] );
tag[rt] = 0;
}
inline void pushup ( const int l, const int r ) {
int rt = id ( l, r ), mid = l + r >> 1, lc = id ( l, mid ), rc = id ( mid + 1, r );
mn[rt] = mn[lc] < mn[rc] ? mn[lc] : mn[rc];
}
inline void update ( const int l, const int r, const int ul, const int ur, const int v ) {
if ( ul <= l && r <= ur ) return pushad ( l, r, v );
int mid = l + r >> 1; pushdn ( l, r );
if ( ul <= mid ) update ( l, mid, ul, ur, v );
if ( mid < ur ) update ( mid + 1, r, ul, ur, v );
pushup ( l, r );
}
inline bool check () { return mn[id ( 1, n )] >= 0; }
} preT, sufT; // ((... and ...)), preT->g, sufT->f.
inline void init ( const int u ) {
siz[u] = 1;
for ( int i = head[u], v; i; i = graph[i].nxt ) {
init ( v = graph[i].to ), siz[u] += siz[v];
if ( siz[son[u]] < siz[v] ) son[u] = v;
}
}
inline void update ( const int u, const int dep, const int k ) {
preT.update ( 1, n, 1, dep, s[u] == '(' ? k : -k );
sufT.update ( 1, n, 1, dep, s[u] == ')' ? k : -k );
}
inline void calc ( const int u, int cnt, const int dep ) {
cnt += s[u] == ')' ? 1 : -1, update ( u, dep, 1 );
if ( sufT.check () ) ans = add ( ans, mul ( siz[u], f[cnt] ) );
if ( preT.check () ) ans = add ( ans, mul ( siz[u], g[-cnt] ) );
for ( int i = head[u]; i; i = graph[i].nxt ) calc ( graph[i].to, cnt, dep + 1 );
update ( u, dep, -1 );
}
inline void coll ( const int u, int cnt, const int dep ) {
cnt += s[u] == '(' ? 1 : -1, update ( u, dep, -1 );
if ( sufT.check () ) f[cnt] = add ( f[cnt], siz[u] );
if ( preT.check () ) g[-cnt] = add ( g[-cnt], siz[u] );
for ( int i = head[u]; i; i = graph[i].nxt ) coll ( graph[i].to, cnt, dep + 1 );
update ( u, dep, 1 );
}
inline void solve ( const int u, const bool keep ) {
for ( int i = head[u], v; i; i = graph[i].nxt ) {
if ( ( v = graph[i].to ) ^ son[u] ) {
solve ( v, false );
}
}
if ( son[u] ) solve ( son[u], true );
if ( s[u] == '(' ) ans = add ( ans, mul ( g[1], n - siz[son[u]] ) );
if ( s[u] == ')' ) ans = add ( ans, mul ( f[1], n - siz[son[u]] ) );
for ( int i = head[u], v; i; i = graph[i].nxt ) {
if ( ( v = graph[i].to ) ^ son[u] ) {
*f = add ( *f, n - siz[v] ), g[0] = add ( *g, n - siz[v] );
update ( u, 1, 1 );
calc ( v, s[u] == ')' ? 1 : -1, 2 );
*f = sub ( *f, n - siz[v] ), g[0] = sub ( *g, n - siz[v] );
update ( u, 1, -1 );
coll ( v, 0, 1 );
}
}
if ( s[u] == '(' ) *f = add ( *f, siz[u] ), -- f, *g ++ = 0;
if ( s[u] == ')' ) *g = add ( *g, siz[u] ), -- g, *f ++ = 0;
if ( ! keep ) {
for ( int i = 0; i <= siz[u]; ++ i ) f[i] = g[i] = 0;
f = aryf + n, g = aryg + n;
}
}
int main () {
scanf ( "%d %s", &n, s + 1 );
for ( int i = 2; i <= n; ++ i ) link ( rint (), i );
init ( 1 );
f = aryf + n, g = aryg + n;
solve ( 1, true );
printf ( "%d\n", ans );
return 0;
}
\(\mathcal{Update}\)
然后你就发现……只需要维护前缀、后缀最大值，与当前前缀、后缀和比较就砍掉 \(\log\) 了 owo！
#include <cstdio>
const int MAXN = 2e5, MOD = 998244353;
int n, ecnt, head[MAXN + 5], siz[MAXN + 5], son[MAXN + 5];
int ans, aryf[MAXN * 2 + 5], aryg[MAXN * 2 + 5], *f, *g;
char s[MAXN + 5];
inline int add ( int a, const int b ) { return ( a += b ) < MOD ? a : a - MOD; }
inline int sub ( int a, const int b ) { return ( a -= b ) < 0 ? a + MOD : a; }
inline int mul ( long long a, const int b ) { return ( a *= b ) < MOD ? a : a % MOD; }
inline void chkmax ( int& a, const int b ) { if ( a < b ) a = b; }
inline int rint () {
int x = 0; char s = getchar ();
for ( ; s < '0' || '9' < s; s = getchar () );
for ( ; '0' <= s && s <= '9'; s = getchar () ) x = x * 10 + ( s ^ '0' );
return x;
}
struct Edge { int to, nxt; } graph[MAXN + 5];
inline void link ( const int s, const int t ) {
graph[++ ecnt] = { t, head[s] };
head[s] = ecnt;
}
inline void init ( const int u ) {
siz[u] = 1;
for ( int i = head[u], v; i; i = graph[i].nxt ) {
init ( v = graph[i].to ), siz[u] += siz[v];
if ( siz[son[u]] < siz[v] ) son[u] = v;
}
}
inline void calc ( const int u, int cnt, int pre, int suf ) {
cnt += s[u] == ')' ? 1 : -1;
chkmax ( pre, -cnt ), chkmax ( suf, cnt );
if ( suf == cnt ) ans = add ( ans, mul ( siz[u], f[cnt] ) );
if ( pre == -cnt ) ans = add ( ans, mul ( siz[u], g[-cnt] ) );
for ( int i = head[u]; i; i = graph[i].nxt ) calc ( graph[i].to, cnt, pre, suf );
}
inline void coll ( const int u, int cnt, int pre, int suf ) {
cnt += s[u] == '(' ? 1 : -1;
chkmax ( pre, -cnt ), chkmax ( suf, cnt );
if ( suf == cnt ) f[cnt] = add ( f[cnt], siz[u] );
if ( pre == -cnt ) g[-cnt] = add ( g[-cnt], siz[u] );
for ( int i = head[u]; i; i = graph[i].nxt ) coll ( graph[i].to, cnt, pre, suf );
}
inline void solve ( const int u, const bool keep ) {
for ( int i = head[u], v; i; i = graph[i].nxt ) {
if ( ( v = graph[i].to ) ^ son[u] ) {
solve ( v, false );
}
}
if ( son[u] ) solve ( son[u], true );
if ( s[u] == '(' ) ans = add ( ans, mul ( g[1], n - siz[son[u]] ) );
if ( s[u] == ')' ) ans = add ( ans, mul ( f[1], n - siz[son[u]] ) );
int pre = s[u] == '(' ? 1 : -1, suf = s[u] == ')' ? 1 : -1;
for ( int i = head[u], v; i; i = graph[i].nxt ) {
if ( ( v = graph[i].to ) ^ son[u] ) {
*f = add ( *f, n - siz[v] ), g[0] = add ( *g, n - siz[v] );
calc ( v, s[u] == ')' ? 1 : -1, pre, suf );
*f = sub ( *f, n - siz[v] ), g[0] = sub ( *g, n - siz[v] );
coll ( v, 0, 0, 0 );
}
}
if ( s[u] == '(' ) *f = add ( *f, siz[u] ), -- f, *g ++ = 0;
if ( s[u] == ')' ) *g = add ( *g, siz[u] ), -- g, *f ++ = 0;
if ( ! keep ) {
for ( int i = 0; i <= siz[u]; ++ i ) f[i] = g[i] = 0;
f = aryf + n, g = aryg + n;
}
}
int main () {
scanf ( "%d %s", &n, s + 1 );
for ( int i = 2; i <= n; ++ i ) link ( rint (), i );
init ( 1 );
f = aryf + n, g = aryg + n;
solve ( 1, true );
printf ( "%d\n", ans );
return 0;
}
最新文章
- Nancy之静态文件处理
- Android-Sqlite数据库的操作
- HTML中禁用表单控件的两种方法readonly与disabled
- 揭开HTTP网络协议神秘面纱系列(三)
- 使用动态SQL语句实现简单的行列转置（动态产生列）
- 数据访问模式之Repository模式
- C语言之原码、反码和补码
- angular控制器之间的传值
- linux kvm虚拟机快速构建及磁盘类型
- [P1020]导弹拦截 (贪心/DP/二分/单调队列)
- yaf项目将500错误打印到页面上
- .NET 序列化成XML, 并且格式化
- VM虚拟机—JVM内存
- Java知多少（14）数组
- mongodb查询数据库中某个字段中的值包含某个字符串的方法
- idou老师教你学Istio 17 : 通过HTTPS进行双向TLS传输
- M1事后分析报告--We have power to change the origin state
- President's Path CodeForces - 416E (最短路,计数)
- 微信小程序接入腾讯云IM即时通讯（会话列表）
- form-inline+form-group 实现表单横排显示（Bootstrap）