CausalVAE: Disentangled Representation Learning via Neural Structural Causal Models

概
主要内容
- 模型
- ELBO
- 关于

Yang M., Liu F., Chen Z., Shen X., Hao J. and Wang J. CausalVAE: disentangled representation learning via neural structural causal models. arXiv preprint arXiv:2004.086975, 2020.

概

隐变量的因果表示.

主要内容

我们通常希望隐变量\(z\)能够表示一些特别的特征, 通过改变\(z\)使得生成的图形某些属性发生相应的变换, 但是这种设定的方式并不具备因果的关系, 比方说

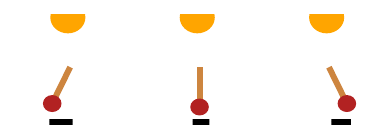
这个摆锤, 其隐变量\(z\)是光照, 摆锤的角度, 影子的长短.

我们可以改变摆锤的角度, 一般的生成模型摆锤的角度变了, 但是光照和影子长短没有发生变化, 实际上由于摆锤角度的变化, 对于的隐变量:影子的长短也应该发生相应的变化以满足物理的规律. 如何把这些因果关系融入到普通的VAE中是本文的独到之处.

模型

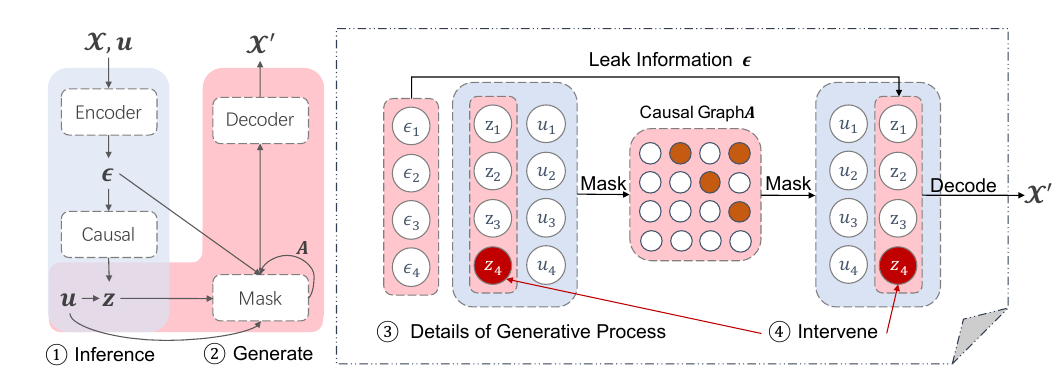
Encoder 部分:

\[\epsilon = h(x, u) + \zeta,
\]

\(\epsilon\)可以看成是一个临时的隐变量;

\[z = (I - A)^{-1} \epsilon.
\]

Decoder部分:

\[z_i = g_i(A_i \circ z) + \epsilon_i,
\]

这一部分是重构\(z\), 正是这一步的存在使得我们能够干预\(z_i\)使得其它的\(z_j\)也发生相应的改变.

\[x = f(z) + \xi.
\]

联合分布为:

\[p_{\theta}(x, z, \epsilon|u) = p_{\theta}(x|z, \epsilon, u)p_{\theta}(\epsilon, z|u), \\
p_{\theta}(x|z,\epsilon,u) = p_{\theta}(x|z) = p_{\xi}(x-f(z)), \\
p_{\theta}(\epsilon,z|u) = p_{\epsilon}(\epsilon) p_{\theta}(z|u), \quad p_{\epsilon}(\epsilon) = \mathcal{N}(0, I), \\
p_{\theta}(z|u) = \prod_{i=1}^n p_{\theta}(z_i|u_i), \quad p_{\theta}(z_i|u_i) = \mathcal{N}(\lambda_1(u_i), \lambda_2^2(\mu_i)).
\]

估计的后验分布为:

\[q_{\phi}(z, \epsilon|x, u) = q(z|\epsilon)q_{\zeta}(\epsilon - h(x, u)), \\
q(z|\epsilon) = \delta (z=(I-A)^{-1}\epsilon).
\]

注: \(z, u, \epsilon \in \mathbb{R}^n, x \in \mathbb{R}^d.\)

ELBO

由此可以推出ELBO:

\[\mathbb{E}_{q_{\mathcal{X}}}[\mathbb{E}_{\epsilon, z\sim q_{\phi}}[\log p_{\theta}(x| z, \epsilon,u)] - \mathbb{D}(q_{\phi}(\epsilon, z|x, u))\| p_{\theta}(\epsilon, z|u)].
\]

由于\(p(z|\epsilon) = \delta(z=(I-A)^{-1}\epsilon)\), 所以上式可以进一步化为:

\[\mathbb{E}_{q_{\mathcal{X}}}[\mathbb{E}_{q_{\phi(z|x,u)}}[\log p_{\theta}(x|z)] - \mathbb{D}(q_{\phi}(\epsilon|x,u)\|p_{\epsilon}(\epsilon))-\mathbb{D}(q_{\phi}(z|x,u)\|p_{\theta}(z|u))]+\mathrm{const}.
\]

关于\(A\)

正如在这儿所论述的, \(A\)需要对应一个有向无环图, 本文采取的策略是:

\[H(A) = \mathrm{tr}((I+\frac{c}{n}A \circ A)^n) - n =0,
\]

这里\(c\)是任意正数.

同时为了满足\(z\)重构, 需要以下条件满足:

\[l_m = \mathbb{E}_{q_{\phi}} \sum_{i=1}^n \|z_i-g_i(A_i \circ z)\|^2 \le \kappa_2,
\]

注: 这里\(z_i\)是重构前的.

特别的, 为了更好地用额外信息(不是很认同, 感觉得看实际情况吧):

\[l_u = \mathbb{E}_{q_{\mathcal{X}}} \|u - \sigma(A^Tu)\|_2^2 \le \kappa_1,
\]

所以最终的损失为:

\[\mathcal{L} = -\mathrm{ELBO} +\alpha H(A) + \beta l_u + \gamma l_m,
\]

注: 本文不像别的方法一样用augmented Lagrange 求解.

注: 作者设计的实验实在是非常有趣.

巴特西

CausalVAE: Disentangled Representation Learning via Neural Structural Causal Models

概

主要内容

模型

ELBO

关于\(A\)

最新文章

热门文章