从\(\mathcal{CSP}\) 爆炸到现在，已经有\(3\)个月了。这三个月间，我——这个小蒟蒻又接触了许多听不懂的东西

\(\mathcal{No.}1\) 字符串\(\mathcal{hash}\):

定义：
- 是把任意长度的输入通过散列算法变换成固定长度的输出，该输出就是散列值。这种转换是一种压缩映射，也就是，散列值的空间通常远小于输入的空间，不同的输入可能会散列成相同的输出，所以不可能从散列值来确定唯一的输入值。简单的说就是一种将任意长度的消息压缩到某一固定长度的消息摘要的函数。
  
  \(emmm\)，还是不懂，跳过
特点：
- 时间复杂度较低
- 运用了前缀和思想
- 对相同数据运算,得到的结果是一样的
- 没法逆运算

实现：

注意：字符串\(hash\)通常使用一个数组来存储\(hash\)值，并需要在计算时乘以\(mod\)（\(mod\)通常取一个较大质数，\(like\) \(131\), \(13331\))，数组通常用 \(long\ long\)

步骤：

首先进行初始化

const int MAXN = 1000010;

const long long Base = 131; //初始化MOD(我这用的是Base)

char Str[MAXN]; //需处理的字符串

long long Hash[MAXN]; //定义hash数组

void Init(const int &Len) {

	for (int i = 1; i <= Len; i ++ ) {

		Hash[i] = Hash[i - 1] * Base + (Str[i] - 'a' + 1);

	}

	return ;

}

怎么样，简不简单？

简单个锤子!!!

随后，我们有时需要查询\(\mathcal{Left}\) ~ \(\mathcal{Right}\) 的 \(hash\) 值，但\(Left\) 不一定等于\(1\)，怎么办？
这时，我们就需要运用前缀和思想，既然要求\(\mathcal{Left}\) ~ \(\mathcal{Right}\)的\(hash\)值，我们是不是可以求出\(1\) ~ \((\mathcal{Left - }1)\)的\(hash\)值与\(1\) ~ \(\mathcal{Right}\) 的\(hash\)值，再进行操作，就完美解决了!!!

上代码

long long Get(const int &Left, const int &Right) {

	return Hash[Right] - Hash[Left - 1] * pow(Base, Right - Left + 1);

}

当然，我们会发现，\(\mathcal{Get}\)函数中调用的的\(pow\)过于耗时，所以我们在初始化时可以定义一个\(\mathcal{Pow}\)数组来存储，实现代码如下：

const int MAXN = 1000010;

const long long Base = 131; //初始化MOD(我这用的是Base)

char Str[MAXN]; //需处理的字符串

long long Hash[MAXN], Pow[MAXN]; //定义hash数组

void Init(const int &Len) {

	Pow[0] = 1; //长度为零时初始化为一

	for (int i = 1; i <= Len; i ++ ) {

		Pow[i] = Pow[i - 1] * Base;

		Hash[i] = Hash[i - 1] * Base + (Str[i] - 'a' + 1);

	}

	return ;

}

long long Get(const int &Left, const int &Right) {

	return Hash[Right] - Hash[Left - 1] * Pow[Base, Right - Left + 1];

}

完美解决!!!

例题：

兔子与兔子 \(\mathcal{OJ}\) \(acwing\)

解析：这道题十分简单，直接套\(hash\)模板

代码

#include <cstdio>

#include <cstring>

const int MAXN = 1000010;

const long long Base = 131;

char Str[MAXN];

long long Hash[MAXN], Pow[MAXN];

void Init(const int &Len) {

	Pow[0] = 1;

	for (int i = 1; i <= Len; i ++ ) {

		Pow[i] = Pow[i - 1] * Base;

		Hash[i] = Hash[i - 1] * Base + (Str[i] - 'a' + 1);

	}

	return ;

}

long long Get(const int &Left, const int &Right) {

	return Hash[Right] - Hash[Left - 1] * Pow[Base, Right - Left + 1];

}

int main () {

	scanf ("%s", Str + 1);

	Len = strlen(Str + 1);

	Init(Len);

	scanf ("%d", &m);

	while (m --) {

		scanf ("%d %d %d %d", &L1, &R1, &L2, &R2);

		if (Get(L1, R1) == Get(L2, R2)) {

			puts("Yes");

		}

		else {

			puts("No");

		}

	}

	return 0;

}

回文子串的最大长度 \(\mathcal{OJ}\) \(acwing\)

解法：前缀和 + 后缀和 + 二分 + \(hash\) 时间复杂度 \(\mathcal{O}(n * log(n))\)
我们发现这道题目数据范围恐怖, 那么只有几个办法可以让我们求解这道题目,那就是\(hash\), 或者是\(\mathcal{O(n)}\)复杂度的\(\mathcal{Manacher}\)算法小蒟蒻不会
\(\mathcal{Manacher}\)由此进入
通过兔子与兔子,我们知道判断两个字符串是否相等,可以使用字符串\(hash\)也就是将字符串算成\(\mathcal{P}\)进制数值,然后区间和判断即可,那么这道题目我们需要一个正的字符串,还需要一个反的字符串,然后如果正字符串等于反的字符串,那么奇数回文串就\(2\ +\ 1\),偶数回文串就直接\(2\)即可.之所以要这么做,因为我们是要回文对不对,我们需要将回文拆解成为一个正字符串和一个反字符串,这样才好处理这道题目.
既然如此,我们可以算出一个前缀和,再算出一个后缀和,然后就可以知道,正字符串和一个反字符串.字符串的\(hash\)值就是这个区间的\(hash\)值和.
算完之后,我们当前就只需要枚举一个\(mid\)中间点,因为所有回文串都是有一个中间点(奇),或者中间区间(偶),然后二分分别寻找这个字符串长度即可,记住不是回文串,回文串的长度,是字符串长度\(*\ 2\ +\ 1\)(奇) 或者是字符串长度\(\ *\ 2\)(偶数).
切记如果说这个最大回文串为\(1\)(也就是所有字符都不一样,比如说\(abcdefg\)),那么输出是\(1\),不是\(3\),奇数回文串=奇数字符串\(*\ 2\ +\ 1\),你们要小心特判这种情况,或者处理二分边界.

代码偷懒不写注释(逃)：

#include <cstdio>

#include <cstring>

#include <algorithm>

using namespace std;

const int MAXN = 100010, Base = 131;

int Len, Total, MaxLen, n;

char Str[MAXN], s[MAXN];

long long Hash_Front[MAXN], Hash_Back[MAXN], Power[MAXN] = {1};

long long Get1(int l, int r) {

	return Hash_Front[r] - Hash_Front[l - 1] * Power[r - l + 1];

}

long long Get2(int l, int r) {

	return Hash_Back[l] - Hash_Back[r + 1] * Power[r - l + 1];

}

bool Check1(int L, int x) {

	return Get1(x - L, x - 1) == Get2(x + 1, x + L);

}

bool Check2(int L, int x) {

	return Get1(x - L, x - 1) == Get2(x, x + L - 1);

}

void Binary_Search(int x) {

	int Left_ = 0, Right_ = min(x - 1, Len - x), Left__ = 0, Right__ = min(x - 1, Len - x + 1);

	while (Left_ < Right_) {

		int Mid = (Left_ + Right_ + 1) >> 1;

		if (Check1(Mid, x) == true) {

			Left_ = Mid;

		}

		else {

			Right_ = Mid - 1;

		}

	}

	MaxLen = max(MaxLen, Left_ * 2 + 1);

	while (Left__ < Right__) {

		int Mid = (Left__ + Right__ + 1) >> 1;

		if (Check2(Mid, x) == true) {

			Left__ = Mid;

		}

		else {

			Right__ = Mid - 1;

		}

	}

	MaxLen = max(MaxLen, Left__ * 2);

	return ;

}

int main () {

	for (int i = 1; i < MAXN; i ++ ) {

		Power[i] = Power[i - 1] * Base;

	}

	while (scanf ("%s", Str + 1) != EOF and Str[1] != 'E') {

		Len = strlen(Str + 1);

		MaxLen = 1;

		Hash_Back[Len + 1] = 0;

		for (int i = 1; i <= Len; i ++ ) {

			Hash_Front[i] = Hash_Front[i - 1] * Base + Str[i] - 'a' + 1;

		}

		for (int i = Len; i >= 1; i -- ) {

			Hash_Back[i] = Hash_Back[i + 1] * Base + Str[i] - 'a' + 1;

		}

		for (int i = 1; i <= Len; i ++ ) {

			Binary_Search(i);

		}

		printf ("Case %d: %d\n", ++ Total, MaxLen);

		getchar();

	}

	return 0;

}

\(hash\)完结!!!

\(\mathcal{No.}2\ \mathcal{Trie}\)树(主要字符串)

实质(我看来)：高效的存储和查找字符串集合的数据结构
思想：从根节点开始，判断有没有该类字符，有就向下，没有就添加叶节点，依次存储，把所有结尾点标记一下，然后用\(\mathcal{Trie}\)高速查找某一个字符出现的次数

模板(字符串)：

void Insert(char *Str) { //简单的初始化插入

	int Root = 0, Len = strlen(Str + 1);

	for (int i = 1; i <= Len; i ++ ) {

		int ID = Str[i] - 'a';

		if (Trie[Root][ID] == 0) { //如果当前字符未出现过，开一个新空间存储

			Trie[Root][ID] = ++ Total;

		}

		Root = Trie[Root][ID]; //进入下一个字符

	}

	return ;

}

bool Find(char *Str) { //查找是否有此单词

	int Root = 0, Len = strlen(Str + 1);

	for (int i = 1; i <= Len; i ++ ) {

		int ID = Str[i] - 'a';

		if (Trie[Root][ID] == 0) { //如果当前字符未匹配成功，返回找不到

			return false;

		}

		Root = Trie[Root][ID]; //进入下一个字符

	}

	return true;

}

例题：

前缀统计 \(\mathcal{OJ}\) \(acwing\)

解析：一想到字符串的前缀,我们就应该想到\(\mathcal{Tire}\)树.这道题目是字典树模板的略微改动,我们发现这道题目和一般\(\mathcal{Tire}\)树的查询不一样,\(\mathcal{Tire}\)树一般查询是看这个字符串是否出现,而这道题目这是统计这个字符串出现的次数.

代码：

#include <cstdio>

#include <cstring>

#include <algorithm>

using namespace std;

const int MAXN = 1e6 + 5;

int n, m, Trie[MAXN][26], Total, End[MAXN];

char Str[MAXN];

void Insert(char *Str) { //简单的初始化插入加处理

	int Root = 0, Len = strlen(Str + 1);

	for (int i = 1; i <= Len; i ++ ) {

		int ID = Str[i] - 'a';

		if (Trie[Root][ID] == 0) { //如果当前字符未出现过，开一个新空间存储

			Trie[Root][ID] = ++ Total;

		}

		Root = Trie[Root][ID]; //进入下一个字符

	}

	End[Root] ++; //统计个数

	return ;

}

bool Find(char *Str) { //查找是否有此单词

	int Root = 0, Len = strlen(Str + 1);

	for (int i = 1; i <= Len; i ++ ) {

		int ID = Str[i] - 'a';

		if (Trie[Root][ID] == 0) { //如果当前字符未匹配成功，返回找不到

			return false;

		}

		Root = Trie[Root][ID]; //进入下一个字符

	}

	return true;

}

int Search(char *Str) {

    int Root = 0, Sum = 0, Len = strlen(Str + 1);

	for (int i = 1; i <= Len; i ++ ) {

		int ID = Str[i] - 'a';

		Root = Trie[Root][ID];

		if (Root == 0) { //如果到了头，就跳出循环

			break;

		}

		Sum += End[Root]; //统计答案

	}

	return Sum; //返回答案

}

int main () {

	scanf ("%d %d", &n, &m);

	for (int i = 1; i <= n; i ++ ) {

		scanf ("%s", Str + 1);

		Insert(Str); //初始化

	}

	while (m --) {

		scanf ("%s", Str + 1);

		printf ("%d\n", Search(Str));

	}

	return 0;

}

\(\mathcal{Trie}\)树完结!!!

\(\mathcal{No.}3\) 单调栈/单调队列：

一种神奇的优化，元素在队列中是单调有序的,由于小蒟蒻理解不够透彻，接不再过多阐述

有兴趣的同学可由此进一步了解

例题：

直方图中最大的矩形 (单调栈) \(\mathcal{OJ}\) \(acwing\)

解析：这道题目是一道单调栈的好题目,首先我们发现,如果说我们确定了这个矩阵的高度的话,那么其实这个矩阵已经确定了,它的\([l,r]\)其实我们已经求出来了,因为矩阵要最大,所以贪心求出\(l,r\)即可,那么我们就可以以这个矩阵的高度为单调性,然后每一次弹出的时候,就计算出矩阵的面积,然后开一个\(\mathcal{Ans}\)记录最大值就好了.

代码：

#include <stack>

#include <cstdio>

using namespace std;

long long Max, Hight, n;

struct node { //定义结构体

	long long h, len;

}t;

int main () {

	while (scanf ("%lld", &n) != EOF && n != 0) { //无限输入

		stack <node> S; //维护一个单调不下降的栈

		Max = -1;

		for (int i = 1; i <= n; i ++) {

			scanf ("%lld", &Hight);

			long long Len = 0;

			while (S.empty () == false and S.top().h > Hight) { //如果单调性被破坏

				t = S.top();

				Len += t.len; // 统计长度

				Max = Max < t.h * Len ? t.h * Len : Max;

				S.pop(); //弹出栈顶元素

			}

			S.push(node{Hight, Len + 1}); //更新答案

		}

		long long Len_ = 0;

		while (S.empty() == false) { //弹出栈内元素

			t = S.top();

			Len_ += t.len;

			S.pop();

			Max = Max < t.h * Len_ ? t.h * Len_ : Max; //更新答案

		}

		printf ("%lld\n", Max); //输出

	}

	return 0;

}

完美解决!!!

最大连续和 (单调队列) \(\mathcal{OJ}\)

解析：由题意设\(dp[i]\)表示到第i个数，不超过\(m\)的最大连续子段和，\(sum[i]\)表示\(1\) ~ \(i\)的前缀和.则容易得到\(dp[i] = max(sum[i] - sum[k]) (i - m <= k <= i)\)，形如此类的递推式可由单调队列维护

代码:

//我程序有个漏洞，如果输入全为负数时，输出为零

//所以才会有特判

#include <queue>

#include <cstdio>

#include <algorithm>

using namespace std;

const int MAXN = 200010;

int n, k, f;

deque <long long> Q; //单调队列一般使用STL中的双端队列

long long a[MAXN], Ans = -0x3f3f3f3f;

int main() {

    scanf("%d %d", &n, &k);

    for (int i = 1; i <= n; i ++ ) {

        scanf("%lld", &a[i]);

        f += a[i] > 0; //统计大于等于零的数的个数

    }

    if (f == 0) { //特判是否全都小于零

        sort(a + 1, a + n + 1);

        printf("%lld\n", a[n]);

        return 0;

    }

    for (int i = 1; i <= n; i ++ ) { //前缀和思想

        a[i] += a[i - 1];

    }

    Q.push_front(0);

    for (int i = 1; i <= n; i ++ ) {

        while (Q.empty() == false and a[i] < a[Q.front()]) { //如果破坏单调性，弹出队顶元素

            Q.pop_front();

        }

        Q.push_front(i); //加入当前元素

        while (Q.empty() == false and i - Q.back() > k) { //若长度大于k，将其弹出

            Q.pop_back();

        }

        Ans = max(a[i] - a[Q.back()], Ans); //更新答案

    }

    printf("%lld\n", Ans);

    return 0;

}

单调栈/单调队列完结!!!

\(\mathcal{No.}4\) 树状数组(\(\mathcal{Binary\ Indexed\ Tree\ /BIT}\))
- 顾名思义，就是用数组来模拟树形结构，正确性证明
- 优点：修改和查询的复杂度都是\(\mathcal{O(log(n))}\)，而且常数相比线段树要小很多，而且容易写。
- 缺点：遇到复杂的区间问题还是不能解决，功能还是有限。
- 例子：
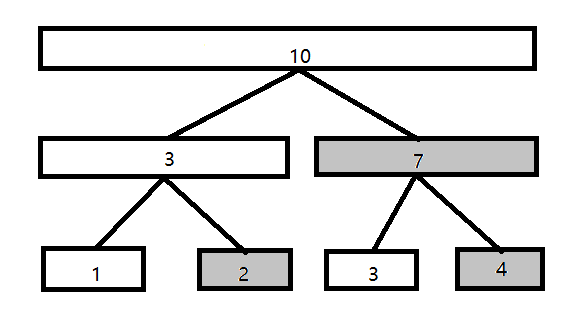
  - 假设有一个数组\(\mathcal{a[]=}\{1,2,3,4\}\),现构造一棵线段树，可得下图：
  - 那么现在看着所构造出来的这棵树来想一个问题，怎样求数组中下标从\(i\)到\(j\)的和？其实\(\mathcal{Sum}\) \((i\) ~ \(j)\)的和可以转化为\(\mathcal{Sum}\) \((1\)~\(j)\) - \(\mathcal{Sum}\) \((1\) ~ \(\mathcal{i -}1)\)。
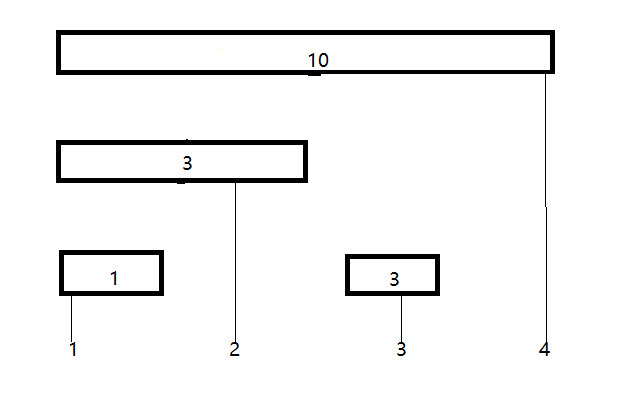
  - 仔细观察上面的线段树，不难发现在求\(1\)到\(x\)的和过程中右儿子\((\)灰色部分的节点\()\)均不需要使用。\(\mathcal{So}\), 我们将这些冗余的节点删去，就可以得到一个树状数组，如下图：
  - 我们可以发现，设节点编号为x，那么这个节点管辖的区间为\(2^k\)（其中\(k\)为\(x\)二进制末尾\(0\)的个数）个元素。因为这个区间最后一个元素必然为\(\mathcal{A[x]}\)。\(\mathcal{So}\), 实现就异常简单。
- 实现：
  1. \(\mathcal{Lowbit:}\)
    
    我们定义一个函数\(\mathcal{Lowbit(x)}:\) 等于上文所提到的\(2^k\), 代码实现\((\)运用计算机补码知识\()\)
```
int Lowbit(const int &x) {

	return (x & (-x));

}
```
    当然,我们也可以用\(\mathcal{define}\)来实现:
```
#define Lowbit(x) ((x) & (-(x)) //注意别删括号,不然会出错
```
  2. 修改:
    
    随后,我们就可根据
    
    结论： \(C\left[ 1\right]\ =\ \sum ^{i}_{(j=i-Lowbit(i) +1)}a[j]\)
    
    \(\mathcal{So}\), 我们可以写出单点修改的代码:
```
void Update(int Index, const int &Number) {

	while (Index <= n) {

		c[Index] += Number;

		Index += Lowbit(Index);

	}

	return ;

}
```
  3. 查询:
    
    既然单点修改的代码已经解决, 查询的代码也就呼之欲出了:
```
int Query(int Index) {

	int Ans = 0;

	while (Index > 0) {

		Ans += c[Index];

		Index -= Lowbit(Index);

	} 

	return Ans;

}
```
  4. 完整代码如下:
```
const int MAXN = 1000010;

#define Lowbit(x) ((x) & (-(x))

int a[MAXN], c[MAXN], n;

void Update(int Index, const int &Number) {

	while (Index <= n) {

		c[Index] += Number;

		Index += Lowbit(Index);

	}

	return ;

}

int Query(int Index) {

	int Ans = 0;

	while (Index > 0) {

		Ans += c[Index];

		Index -= Lowbit(Index);

	} 

	return Ans;

}
```
- 例题:
  - 树状数组 \(1\) ：单点修改，区间查询 \(\mathcal{OJ}\) \(luogu\)
    - 一道模板题,直接套树状数组就行了
    - 代码就不展示了
  - 二维树状数组 \(1\)：单点修改，区间查询 \(\mathcal{OJ}\)
    - 思路:这是一道二维树状数组废话, 我们可以将其理解为一个一维树状数组再套一个一维树状数组, 就迎刃而解
    - \(\mathcal{Update}\)与\(\mathcal{Query}\)代码如下:
```
const int MAXN = 5050;

#define LowBit(x) (x & (-x))

int n, m;

long long Tree[MAXN][MAXN]; //注意long long

void Update(const int &x, const int &y, const long long &k) {

	for (int i = x; i <= n; i += LowBit(i)) {

		for (int j = y; j <= m; j += LowBit(j)) {

			Tree[i][j] += k;

		}

	}

	return ;

} 

long long Query(const int &x, const int &y) {

	long long Total = 0;

	for (int i = x; i > 0; i -= LowBit(i)) {

		for (int j = y; j > 0; j -= LowBit(j)) {

			Total += Tree[i][j];

		}

	}

	return Total;

}
```
  - 树状数组 \(2\) ：区间修改，单点查询 \(OJ\) \(luogu\)
    - 解析:这道题需要运用差分思想.设\(c[i] = a[i] - a[i - 1]\), \(\mathcal{So}, a[i] = \sum ^ i _{(j = 1)} c[j]\).
    - 当我们对区间\(\mathcal{[Left, Right]}\)整体加\(k\)时,通过差分思想, 我们可以将其转化\(\mathcal{c[Left]}\)加上\(k\)与\(\mathcal{c[Right}\)\(+1]\)减去\(k\), 再用树状数组维护\(c\)数组的前缀和
    - 代码就请诸位自己实现
  - 树状数组 \(3\) ：区间修改，区间查询 \(\mathcal{OJ}1\) \(\mathcal{OJ}2\) \(luogu\)
    - 一道线段树模板题
    - 这道题用线段树固然清晰明了,但既然他又树状数组前缀,我们也要想想它如何用树状数组实现.
    - 思路:
      
      在区间修改单点查询的基础上,设原数组\(a[]\), 差分数组\(\mathcal{Tree[]}\)
      
      于是,我们有 \(a[i] = \sum^i_{(j = 1)}\mathcal{Tree[j]}\)
      
      进而, 我们有 \(\sum^n_{(i = 1)}a[i] = \sum^n_{(i = 1)}\sum^i_{(j = 1)}\mathcal{Tree[j]}\)
      
      \(\Rightarrow \sum^n_{(i = 1)}a[i] = \sum^n_{(i = 1)}\mathcal{Tree[i]} * (n - i + 1)\)
      
      \(∴ \sum^n_{(i = 1)}a[i] = \sum^n_{(i = 1)}\mathcal{Tree[i]} * n - \sum^n_{(i = 1)}\mathcal{Tree[i]} * (i - 1)\)
      
      所以,我们可以在维护一个树状数组存储\(\mathcal{Tree[i]} * (i - 1)\)即可
    - 代码:
```
#include <cstdio>

#include <algorithm>

using namespace std;

const int MAXN = 1000005;

#define Lowbit(x) (x & -x)

int n, Tree, l, r, s, m;

long long a[MAXN], Tree1[MAXN], Tree2[MAXN], k;

void Update(long long *Tree, int k, long long x) {

   for (; k <= n; k += Lowbit(k)) {

   	Tree[k] += x;

   }

   return ;

}

long long Sum(long long *Tree, int k) {

   long long Ans = 0;

   for (; k > 0; k -= Lowbit(k)) {

   	Ans += Tree[k];

   }

   return Ans;

}

int main () {

   scanf ("%d %d", &n, &m);

   for (int i = 1; i <= n; i ++ ) {

   	scanf ("%lld", &a[i]);

   	Update(Tree1, i, a[i] - a[i - 1]);

   	Update(Tree2, i, (a[i] - a[i - 1]) * (i - 1));

   }

   while (m --) {

   	scanf ("%d", &s);

   	if (s == 1) {

   		scanf ("%d %d %lld", &l, &r, &k);

   		Update(Tree1, l, k);

   		Update(Tree1, r + 1, -k);

   		Update(Tree2, l, k * (l - 1));

   		Update(Tree2, r + 1, -k * r);

   	}

   	else {

   		scanf ("%d %d", &l, &r);

   		printf("%lld\n", r * Sum(Tree1, r) - Sum(Tree2, r) - (l - 1) * Sum(Tree1, l - 1) + Sum(Tree2, l - 1));

   	}

   }

   return 0;

}
```
- 树状数组完结

\(\mathcal{No.}5\) 分治\((\)二分，三分\()\)

分治简而言之就是分而治之\(——\)将一个规模很大的问题分成若干个规模较小的子问题，并由子问题的解推出全局最优解。
二分查找针对的是一个有序的数据集合，每次通过跟区间中间的元素对比，将待查找的区间缩小为之前的一半，直到找到要查找的元素，或者区间缩小为\(0\)，但是，如果要求出凸函数或凹函数的最值时，二分就毫无用武之地了，这时，我们就可以用三分法来求出答案。 \((\mathcal{Such}\) \(as\) \(this\)\()\)

代码实现：

二分：

void Binary_Search(int Left, int Right) { //整数域上的二分

	while (Left < Right) {

		int Mid = (Left + Right + 1) >> 1;

		if (Check(Mid) == true) {

			…… //进行操作

		}

		else {

			…… //进行操作

		}

	}

	printf ("%d\n", Left);

	return ;

}



const double eps = 1e-10; //通常用一个极小值来减小误差

void Binary_Search(double Left, double Right) { //实数域上的二分

	while (Left < Right) {

		double Mid = (Left + Right) / 2;

		if (Check(Mid) == true) {

			…… //进行操作

		}

		else {

			…… //进行操作

		}

	}

	printf ("%lf\n", Left);

	return ;

}

三分：

int Find(int Left, int Right) {

	while (Left < Right) {

		int Mid1 = Left + (Right - Left) / 3, Mid2 = Right - (Right - Left) / 3;

		if (Check(Mid1) > Check(Mid2)) {

			…… //进行操作

		}

		else {

			…… //进行操作

		}

	}

	return Left;

}

实数域代码不见了

例题：

\(\mathcal{Sumdiv}\) \(\mathcal{OJ}\) \(\mathcal{POJ}\)

解析：这道题乍一看很难，实际上只要你有一点数学基础，再加一个快速幂就可迎刃而解

设 \(n = \prod^m_{(i=1)}p^{a_i}_i\)，因数和为\(\mathcal{Sum}\)

\(\mathcal{=>Sum}=\prod^m_{(i=1)}\sum^{a_i}_j p^j_i\)

而\(\sum^n_{\left(i = 1\right)} x^i= \Big\{^{\sum^{(n / 2)}_{(i = 1)} x^i *\ (x^{(n / 2)}\ +\ 1)\ \ (n\mod 2=0)}_{(\sum^{(n-1)}_{(i=1)}x^i)\ *\ x^n\ (n\mod2=1)}\)

所以我们可以得出代码：

#include <cstdio>

const long long MOD = 9901, MAXN = 1010;

long long Ans = 1, a, b, num[MAZXN], t[MAXN];

int cnt;

long long Qkpow(long long Base, long long x) { //快速幂模板

	long long Total = 1;

	while (x) {

		if (x & 1) {

			Total = (Total * Base) % MOD;

		}

		Base = (Base * Base) % MOD;

		x >>= 1;

	}

	return Total;

}

long long Sum(long long x, long long n) { //求x^1 + x^2 + …… + x^n的和

	if (n == 1) { //边界条件

		return x;

	}

	if (n & 1) { //n mod 2 == 1的情况

		return (Qkpow(x, n) + Sum(x, n / 2) % MOD * (1 + Qkpow(x, n / 2))) % MOD;

	}

	return (Sum(x, n / 2) % MOD * (1 + Qkpow(x, n / 2))) % MOD;

}

int main () {

	scanf ("%lld %lld", &a, &b);

	if (b == 0) { //特判1

		printf ("%lld\n", 1);

		return 0;

	}

	if (a == 0) { //特判2

		printf ("%lld\n", 0);

		return 0;

	}

	for (long long i = 2; i <= a; i ++) { //筛选因数

		if (a % i == 0) {

			num[++ cnt] = i;

			while (a % i == 0) { //存储该因数以及个数

				a /= i;

				t[cnt] ++;

			}

		}

	} 

	for (long long i = 1; i <= cnt; i ++) { //进行计算

		Ans = (Ans * (1 + Sum(num[i], t[i] * b) % MOD)) % MOD;

	}

	printf ("%lld\n", Ans);

	return 0;

}

曲线 \(\mathcal{OJ}\) \(\mathcal{luogu}\)

解析:\(luogu\)居然有用模拟退火的巨佬，作为一个小蒟蒻，我也只能在此想一想三分。观察题目图像得\(\mathcal{Function(x)}\)函数是一个下凸函数, \(\mathcal{So, }\)我们可以发现在函数上任意取四个点纵坐标\(x1<x2<x3<x4\), 且最小值取值范围在\([x1,x4]\)之间，设最小值纵坐标为\(x_{min}\)。
- 若\(\mathcal{Function}(x1)<\mathcal{Function}(x2)\)，则\(x_{min}\in[x1,x2]\)，因为若\(\mathcal{Function}(x1)<\mathcal{Function}(x2)\)，必有\(\mathcal{Function}(x1)<\mathcal{Function}(x2)<\mathcal{Function}(x3)<\mathcal{Function}(x4)\)；
- 同理，若\(\mathcal{Function}(x3)>\mathcal{Function}(x4)，x_{min}\in[x3,x4]\)。
- 若\(\mathcal{Function}(x1)>\mathcal{Function}(x2)\ and\ \mathcal{Function}(x2)<\mathcal{Function}(x3)\)，则\(x_{min}\in[x1,x3]\)，因为下凸函数有且仅有一个低谷，并且下凸函数的最小值在低谷中。
- 同理，若\(\mathcal{Function}(x4)>\mathcal{Function}(x3)\ and\ \mathcal{Function}(x3)<\mathcal{Function}(x2)，x_{min}\in[x2,x4]\)。
- 最后就只剩下一种情况了，此时\(x_{min}\in[x2,x3]\)。

代码(极为丑陋)：

#include <cstdio>

#include <algorithm>

using namespace std;

const int MAXN = 10010;

const double INF = 2e9;

int T, n;

double a[MAXN], b[MAXN], c[MAXN], Function_[5];

double Function(double x) { //计算函数值

	double Total = -INF;

	for (int i = 1; i <= n; i ++ ) {

		Total = max(Total, a[i] * x * x + b[i] * x + c[i]);

	}

	return Total;

}

int main() {

	scanf ("%d", &T);

	while (T --) { //多组数据

		scanf ("%d", &n);

		for (int i = 1; i <= n; i ++ ) {

			scanf ("%lf %lf %lf", &a[i], &b[i], &c[i]);

		}

		double Left = 0, Right = 1000;

		while (Left + 1e-10 < Right) { //减小精度误差

			double Mid1 = (Left + Left + Right) / 3, Mid2 = (Left + Right + Right) / 3; //三分

			Function_[0] = Function(Left);

			Function_[1] = Function(Mid1);

			Function_[2] = Function(Mid2);

			Function_[3] = Function(Right);

			if (Function_[0] < Function_[1]) {

				Right = Mid1;

			}

			else if (Function_[3] < Function_[2]) {

				Left = Mid2;

			}

			else if (Function_[0] > Function_[1] and Function_[2] > Function_[1]) {

				Right = Mid2;

			}

			else if (Function_[3] > Function_[2] and Function_[2] < Function_[1]) {

				Left = Mid1;

			}

			else {

				Left = Mid1;

				Right = Mid2;

			}// 同分析

		}

		printf ("%.4lf\n", Function(Left)); //输出函数值

	}

    return 0;

}

分治完结!!!

\(\mathcal{No.}6\ \ \mathcal{DP——}0/1\)背包
- 问题描述：
  
  给定\(\mathcal{n}\)个物品，体积与价值分别为\(\mathcal{Volume[i],\ Value[i]}\), 有一个容量为\(\mathcal{W}\)的背包，问背包中装入的物品最大价值为多少(每种物品要么选一个，要么不选)?
  
  \(\mathcal{eg: n}=4,\mathcal{W}=8\)
\(\mathcal{i(}\) 物品编号 \()\) \(\mathcal{Volume(}\) 体积 \()\) \(\mathcal{Value(}\) 容积 \()\)

\(1\) \(2\) \(3\)

\(2\) \(3\) \(4\)

\(3\) \(4\) \(5\)

\(4\) \(5\) \(6\)
- 思路：
  1. 设\(\mathcal{X_i}\)表示第\(i\)件物品取\(\mathcal{X_i}\)件\((\mathcal{X_i}\in[0,1])\)， \(\mathcal{DP(i,j)}\)表示当前背包容量\(j\)，前\(i\)个物品最佳组合对应的价值
  2. 建立模型，即求\(\max(\sum^n_{(i=1)}\mathcal{X_i * Value_i})\)
  3. 寻找约束条件，\(\sum^n_{(i=1)}\mathcal{X_i*Volume_i}\le \mathcal{V}\)
  4. 寻找状态转移方程：易知，遇到当前商品有两种情况
    
    1)装不下：当前最优质就等于前\(i-1\)个物品的最优值，即\(\mathcal{DP}(i,j)=\mathcal{DP}(i-1,j)\)
    
    2)装得下：但装了不一定更优于当前最优价值，所以在装与不装之间选择最优的一个，即\(\mathcal{DP}(i,j)=\max(\mathcal{DP}(i-1,j),\mathcal{DP}(i-1,j-\mathcal{Volume_i})+Value_i)\)
    
    于是，我们可以得出状态转移方程：
    
    \(\mathcal{DP}(i,j)=\bigg\{^{\mathcal{DP}(i-1,j)\ (j\ <\ \mathcal{Volume_i})}_{\max(\mathcal{DP}(i-1,j),\ \mathcal{DP}(i-1,j-\mathcal{Volume_i})+Value_i)\ (j\geq\mathcal{Volume_i})}\)
  5. 边界:\(\mathcal{DP}(0,j) = \mathcal{DP}(i,0)=0\)
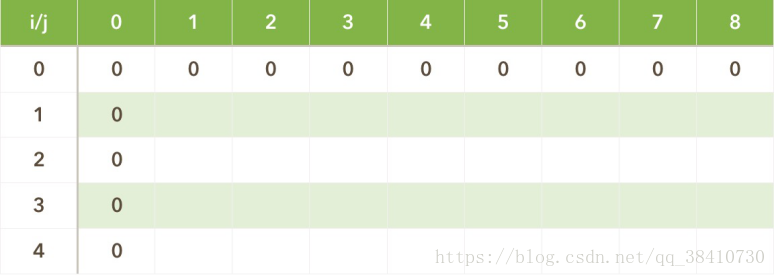
  6. 接着，我们用前面的例子来模拟一遍填表工作：
    
    随后一行一行地填表……最终的表如下：
    
    答案为\(\mathcal{DP}(4, 8)=10\)
    
    代码如下：
```
for (int i = 1; i <= n; i ++ ) {

	for (int j = 1; j <= m; j ++ ) {

		if (j <= Volume[i]) {

			DP[i][j] = DP[i - 1][j];

		}

		else {

			DP[i][j] = max(DP[i - 1][j], DP[i - 1][j - Volume[i]] + Value[i]);

		}

	}

}
```
  - 优化：由以上分析可得，\(\mathcal{DP}\)时间复杂度为\(\mathcal{O}(n^2)\), 空间复杂度为\(\mathcal{O}(n*m)\), 但是，时间复杂度已无法优化。\(\mathcal{So}\)，我们就从空间复杂度下手。
  1. 滚动数组：观察状态转移方程知当前第\(i\)层的答案只能由第\(i - 1\)层得到。所以，我们只用开大小为\(\mathcal{O}(2*m)\)。状态转移方程为：
    
    \(\mathcal{DP}[i\&1][j]=\bigg\{^{\mathcal{DP}[(i - 1)\&1][j]\ (j < \mathcal{Volume_i})}_{\max(\mathcal{DP}[(i-1)\&1][j],\ \mathcal{DP}[(i-1)\&1][j-\mathcal{Volume_i}]+\mathcal{Value_i})\ (j\geq \mathcal{Volume_i})}\)
    
    代码实现如下：
```
for (int i = 1; i <= n; i ++ ) {

	for (int j = 1; j <= m; j ++ ) {

		if (j < Volume[i]) {

			DP[i & 1][j] = DP[(i - 1) & 1][j];

		}

		else {

			DP[i & 1][j] = max(DP[(i - 1) & 1][j], DP[(i - 1) & 1][j - Volume[i]] + Value[i])

		}

	}

}
```
  2. 一维数组：由之前的分析可以看出，每次操作前都将\(\mathcal{DP}[i - 1][j]\)拷贝至\(\mathcal{DP}[i][j]\)，\(So\)我们可以去掉第一维。(但为了\(0-1\)背包的正确性，内层循环必须倒序循环)状态转移方程:
    
    \(\mathcal{DP}[j]=\max(\mathcal{DP}[j]，\mathcal{DP}[j-\mathcal{Volume_i}] + \mathcal{Value_i})\)
    
    代码如下:
```
for (int i = 1; i <= n; i ++ ) {

	for (int j = m; j >= Volume[i]; j -- ) {

		DP[j] = max(DP[j], DP[j - Volume[i]] + Value[i]);

	}

}
```

\(\mathcal{i(}\) 物品编号 \()\)	\(\mathcal{Volume(}\) 体积 \()\)	\(\mathcal{Value(}\) 容积 \()\)
\(1\)	\(2\)	\(3\)
\(2\)	\(3\)	\(4\)
\(3\)	\(4\)	\(5\)
\(4\)	\(5\)	\(6\)

例题：

选择卡片 \(\mathcal{OJ}\)

解析：这道题题意简洁明了。首先，设要求构成\(\mathcal{Avg}\), \(\mathcal{DP}[i][j]\)代表使用\(i\)个数可以凑出\(j\)的方案总数。由此，我们可以推出状态转移方程：

\(\mathcal{DP}[i][j]=\sum^{n}_{(k=i)}\mathcal{DP}[i-1][j-a[k]]\ (a[k]\leq j)\)

\(\mathcal{Sum}=\sum^{n}_{(i=1)}DP[i][i*Avg]\)

\(\mathcal{DP}[0][0]=1\)

代码就异常简单了。请往下看：

#include <cmath>

#include <cstdio>

const int MAXN = 60;

int n, Avg, x[MAXN];

long long DP[MAXN][MAXN * MAXN] = {{1}}, Ans_;

int main () {

	scanf ("%d %d", &n, &Avg);

	for (int i = 1; i <= n; i ++) {

		scanf ("%d", &x[i]);

	}

	for (int i = 1; i <= n; i ++) { //枚举当前物品

		for (int j = i; j >= 1; j --) { //枚举物品个数

			for (int k = j * 50; k >= x[i]; k --) { //枚举背包容量

				DP[j][k] += DP[j - 1][k - x[i]];

			}

		}

	}

	for (int i = 1; i <= n; i ++) { //统计答案

		Ans_ += DP[i][i * Avg];

	}

	printf ("%lld\n", Ans_);

	return 0;

}

\(0/1\)背包完结!!!

\(\mathcal{No.}7\ \mathcal{DP}——\)完全背包

问题描述：

给定\(\mathcal{n}\)个物品，质量与价值分别为\(\mathcal{Weight[i],\ Value[i]}\), 有一个最大承载量为\(\mathcal{W}\)的背包，问背包中装入的物品最大价值为多少?(每种物品有无数件)
思路：

与\(0-1\)背包极为相似。我们只需将\(0-1\)背包的内层循环改为从小到大循环，便完美解决。代码如下：
```
for (int i = 1; i <= n; i ++ ) {

		for (int j = Weight[i]; j <= W; j ++ ) {

			DP[j] = max(DP[j], DP[j - Weight[i]] + Value[i]);

		}

	}
```
时间复杂度为 \(\mathcal{O}(n*\mathcal{W})\), 空间复杂度为\(\mathcal{O}(\mathcal{W})\)

例题：

\(\mathcal{FATE}\) \(\mathcal{OJ}\) \(\mathcal{HDU}\)

思路：这道题就是一道裸的完全背包。首先，我们考虑状态如何定义\(——\mathcal{DP}[i][j]\)表示杀了第\(i\)个怪忍耐度耗去\(j\)时最大能得到的经验值

状态转移方程如下：

\(\mathcal{DP}[i][j]=\max(\mathcal{DP}[i][j],\mathcal{DP}[i-1][j-b[k]]+a[k])\)

代码如下：

#include <cstdio>

#include <cstring>

#include <algorithm>

using namespace std;

const int MAXN = 105;

int DP[MAXN][MAXN], a[MAXN], b[MAXN], n, m, k, s;

int main () {

	while (scanf ("%d %d %d %d", &n, &m, &k, &s) != EOF) { //无限输入

		memset (DP, 0, sizeof DP); //初始化

		for (int i = 1; i <= k; i ++ ) {

			scanf ("%d %d", &a[i], &b[i]);

		}

		for (int i = 1; i <= k; i ++ ) { //枚举第i种怪物

			for (int j = 1; j <= s; j ++) { //枚举这是第几个怪

				for (int l = m; l >= b[i]; l --) { //枚举

					DP[j][l] = max(DP[j][l], DP[j - 1][l - b[i]] + a[i]); //状态转移方程

				}

			}

		}

		bool Flag = false;

		for (int i = 0; i <= m; i ++) {

			for (int j = 1; j <= s; j ++) {

				if (DP[j][i] >= n) { //枚举每个状态找最优

					printf ("%d\n", m - i);

					Flag = true;

					break;

				}

			}

		}

		if (Flag == false) { //判断是否无解

			printf ("-1\n");

		}

	}

	return 0;

}

完全背包完结!!!

\(\mathcal{No.}8\) \(\mathcal{DFS}\)序\(/\)欧拉序\((\)重点\(\mathcal{DFS}\)序\()\)

定义：
- \(\mathcal{DFS}\)序：是指将一棵树被\(\mathcal{DFS}\)时所经过的节点顺序（不绕回原点）。
- 欧拉序：就是从根结点出发，按\(\mathcal{DFS}\)的顺序再绕回原点所经过所有点的顺序。
作用
- 通过\(\mathcal{DFS}\)序判断\(v\)节点是否在\(u\)节点的子树内。
- 通过欧拉序求\(u\)和\(v\)的最近公共祖先，子树权值和等。

\(\mathcal{DFS}\)序\(:\)

性质： 同一棵子树的编号会连在一起
解决问题实例：
- \(1)\) 将子树内的节点权值加\(\mathcal{V}\)
- \(2)\) 查询某子树的最大值

代码实现

void DFS(int Node, int Father) {

    In[Node] = ++ Cur; //节点进入时编号

    for (int i = 0; i < Graph[Node].size(); i++) {

        if (Graph[Node][i] != Father) {

            DFS(Graph[Node][i], Node); //递归遍历子树

        }

    }

    Out[Node] = Cur; //节点离开时编号

    return;

}

欧拉序：

代码实现\((\)与\(\mathcal{DFS}\)序大同小异\():\)

void DFS(const int &Node, const int &Father) {

	Euler[++ cnt] = Node; //进入时记录

	for (int i = 0; i < Tree[Node].size(); ++ i ) {

		if (Tree[Node][i] ^ Father) {

			DFS(Tree[Node][i], Node);

		}

	}

	Euler[++ cnt] = Node;

	return ;

}

例题：

\(\mathcal{DFS}\)序\(1\) \(\mathcal{OJ}\) \(\mathcal{LOJ}\)

解析\(:\)

这道题算法为\(\mathcal{DFS}\)序\(+\)树状数组

在求出此树的dfs序之后，子树是一段连续的区间，可以将对子树的区间操作直接化为对应序列的区间操作

#include <cstdio>

#include <vector>

using namespace std;

const int MAXN = 1000010;

#define LowBit(x) ((x) & -(x))

long long Tree[MAXN];

vector<int> Graph[MAXN];

int In[MAXN], Out[MAXN], Cur, u, v;

int n, m, Root, a, x, c, Value[MAXN];

void DFS(int Node, int Father) { //求DFS序

    In[Node] = ++Cur;

    for (int i = 0; i < Graph[Node].size(); i++) {

        if (Graph[Node][i] != Father) {

            DFS(Graph[Node][i], Node);

        }

    }

    Out[Node] = Cur;

    return;

}

void UpDate(int x, int k) { //树状数组修改

    while (x <= n) {

        Tree[x] += k;

        x += LowBit(x);

    }

    return;

}

long long Get_Sum(int x) { //树状数组查询

    long long Total = 0;

    while (x > 0) {

        Total += Tree[x];

        x -= LowBit(x);

    }

    return Total;

}

int main() {

    scanf("%d %d %d", &n, &m, &Root);

    for (int i = 1; i <= n; i++) {

        scanf("%d", &Value[i]);

    }

    for (int i = 1; i < n; i++) { //建树

        scanf("%d %d", &u, &v);

        Graph[u].push_back(v);

        Graph[v].push_back(u);

    }

    DFS(Root, 0);

    for (int i = 1; i <= n; i++) { //将对树的操作当成对当前序列的操作

        UpDate(In[i], Value[i]);

    }

    while (m--) {

        scanf("%d %d", &c, &a);

        if (c == 1) {

            scanf("%d", &x);

            UpDate(In[a], x);

        }

        else {

            printf("%lld\n", Get_Sum(Out[a]) - Get_Sum(In[a] - 1)); //前缀和思想

        }

    }

    return 0;

}

\(\mathcal{DFS}\)序\(/\)欧拉序完结!!!
还不清楚的小盆友可以看一下这篇文章 \(\mathcal{DFS}\)序和欧拉序

\(\mathcal{No.}9\) 树形\(\mathcal{DP}\)

就是在树形结构基础上的\(\mathcal{DP}\), 一般计算顺序为

根节点\(\Rightarrow\)叶节点 \(or\) 叶节点\(\Rightarrow\)根节点

一般实现框架

vector <int> Tree[MAXN]; //定义存图的数组

void DFS(const int &Node/*当前节点*/, const int &Father/*父节点*/) { //一般用递归实现

	for (int i = 0; i < Tree[Node].size(); ++ i ) {

		int Child = Tree[Node][i];

		if (Child == Father) {//如果是父节点就跳过

			continue;

		}

		DFS(Child, Node); //一直递归至叶节点

		/*

			进行需要的操作

		*/

	}

	return ;

}

废话不多说，就在例题中领悟树形\(\mathcal{DP}\)的精髓吧

没有上司的舞会 \(\mathcal{OJ}1\) \(\mathcal{OJ}2\) \(\mathcal{OJ}3\) \(\mathcal{luogu}\) 重题好多
- 思路：
  
  这是一道赤裸裸的树形\(\mathcal{DP}\)。我们首先定义\(\mathcal{DP}[i][j]\ (i\in[0,1],\ i=0\)表示放\(,\ i=1\)表示不放\()\)代表在第\(j\)个人是否来时的总共可参加舞会的最多人数。当\(i=0\)时，这个节点的人就不会来，它的所有直接下属便可来可不来。当\(i=1\)时，当前节点的人回来，它的所有直接下属都不能来。
  
  于是，动态转移方程为
  
  \(\mathcal{DP}[0][j]=\sum^{\mathcal{Tree[j].size()}-1}_{k=0}(\max(\mathcal{DP}[0][\mathcal{To}], \mathcal{DP}[1][\mathcal{To}])\ (\mathcal{To}=\mathcal{Tree}[j][k])\)
  
  \(\mathcal{DP}[1][j]=\sum^{\mathcal{Tree[j].size()}-1}_{k=0}\mathcal{DP}[0][\mathcal{To}]\ (\mathcal{To}=\mathcal{Tree}[j][k])\)
  
  初始化\(\mathcal{DP}[1][j]=a[j]\ (a\)为开心值\()\)，\(\mathcal{DP}[0][j]=0\)
- 计算顺序为从叶节点至根节点。\(\mathcal{So}\)，代码如下\(:\)
```
#include <cstdio>

#include <vector>

#include <algorithm>

using namespace std;

const int MAXN = 6010;

vector <int> Graph[MAXN]; //定义存图数组

int n, k, l, a[MAXN], DP[2][MAXN], Du[MAXN], Root;

void DFS(int x) {

	for (int i = 0; i < Graph[x].size(); i ++) {

		DFS(Graph[x][i]); //先行递归叶节点

		DP[1][x] += DP[0][Graph[x][i]];

		DP[0][x] += max(DP[0][Graph[x][i]], DP[1][Graph[x][i]]);

		//动态转移方程

	}

	return ;

}

int main () {

	scanf ("%d", &n);

	for (int i = 1; i <= n; i ++) {

		scanf ("%d", &a[i]); //得到开心值

		DP[1][i] += a[i];

	}

	for (int i = 1; i <= n; i ++) {

		scanf ("%d %d", &l, &k);

		Graph[k].push_back(l); //建树

		Du[l] ++;

	}

	for (int i = 1; i <= n; i ++) { //找到大Boss

		if (Du[i] == 0) {

			Root = i;

			break;

		}

	}

	DFS(Root); //递归求解

	printf ("%d\n", max(DP[1][Root], DP[0][Root])); //判断大Boss是否来，取其最大值

	return 0;

}
```

选课 \(\mathcal{OJ}1\) \(\mathcal{OJ}2\) \(\mathcal{OJ}3\) \(\mathcal{OJ}4(\)略有不同\()\) \(\mathcal{luogu}\) 重题好多++

思路：背包\(+\)树形\(\mathcal{DP}\)，详见代码

代码：

#include <cstdio>

#include <vector>

#include <iostream>

#include <algorithm>

using namespace std;

const int MAXN = 310; 

vector <int> Tree[MAXN];

int n, m, Value[MAXN], s, DP[MAXN][MAXN];

int Read() { //友好的读优

    int x = 0, f = 0;

	char c = getchar();

    while (isdigit(c) == false) {

        f = (c == '-' ? 1 : f);

        c = getchar();

    }

    while (isdigit(c) == true) {

        x = (x << 1) + (x << 3) + (c ^ 48);

        c = getchar();

    }

    return f ? -x : x;

}

void DFS(int x) { //递归求解

	for (int i = 0; i < Tree[x].size(); i ++) {

		int Son = Tree[x][i];

		DFS(Son); //递归至叶节点

		for (int j = m + 1; j >= 2; j --) { //背包思想,枚举背包当前容量(还可学几门课)

			for (int k = j - 1; k > 0; k --) { //0-1背包

				DP[x][j] = max(DP[x][j], DP[x][j - k] + DP[Son][k]);

			}

		}

	}

	return ;

}

int main () {

	n = Read();

	m = Read();

	for (int i = 1; i <= n; i ++) {

		s = Read();

		DP[i][1] = Read();

		Tree[s].push_back(i); //建树

	}

	DFS(0); //默认必须学0节点

	printf ("%d\n", DP[0][m + 1]); //输出答案

	return 0;

}

树形\(\mathcal{DP}\)完结!!!

\(\mathcal{No.}10\) 区间\(\mathcal{DP}\)
- 定义:就是在区间上进行动态规划，求解一段区间上的最优解。主要是通过合并小区间的最优解进而得出整个大区间上最优解的\(\mathcal{DP}\)算法。类似分治
- 思路：
  - 求解在一个区间上的最优解，那么可以把这个区间分割成许多小区间，求解每个小区间的最优解，再合并即可。所以在代码实现上可以枚举区间长度\(\mathcal{Len}\)为每次分割成的小区间长度(由短到长不断合并)，内层枚举该长度下可以的起点。然后在这个起点终点之间枚举分割点，求解这段小区间在某个分割点下的最优解
  - 代码框架：
```
for (int Len = 2; Len <= n; Len ++ ) { //枚举长度

	for (int i = 1; i <= n - Len + 1; i ++ ) { //枚举起点

		int j = i + Len - 1; //得到终点

		for (int k = i; k < j; k ++ ) { //枚举断点

		 /*

		 进行需要的操作

		 */

		}

	}

}
```
- 例题：
  - 能量项链 \(\mathcal{OJ}1\) \(\mathcal{OJ}2\) \(\mathcal{OJ}3\) \(\mathcal{OJ}4\) \(\mathcal{luogu}\) \(\mathcal{LOJ}\) 重题好多++
    - 思路：这道题异常简单，直接套上模板即可(\(luogu\)居然是绿的)详见代码
    - 代码：
```
#include <cstdio>

#include <iostream>

using namespace std;

int n, Ans, a[405], DP[405][405];

int main() {

	scanf ("%d", &n);

	for (int i= 1; i <= n; i ++ ) {

		scanf ("%d", &a[i]);

		a[i + n] = a[i]; //破环为链!!!

	}

	for(int i = 2; i < 2 * n; i ++ ) { //另外的写法

		for (int j = i - 1; j >= 1 && i - j < n; j -- ) {

			for (int k = j; k < i; k ++ ) {

				DP[j][i] = max(DP[j][i], DP[j][k] + DP[k + 1][i] + a[i + 1] * a[j] * a[k + 1]);

				Ans = max(DP[j][i], Ans);

			}

		}

	}

	printf ("%d\n", Ans); //输出答案

	return 0;

}
```
- 区间\(\mathcal{DP}\)水完!!!

------------------------\(\mathcal{The\ End}\) ------------------------

巴特西

总结(2019CSP之后)，含题解

\(\mathcal{No.}1\) 字符串\(\mathcal{hash}\):

定义：

特点：

实现：

例题：

兔子与兔子 \(\mathcal{OJ}\) \(acwing\)

回文子串的最大长度 \(\mathcal{OJ}\) \(acwing\)

\(\mathcal{No.}2\ \mathcal{Trie}\)树(主要字符串)

例题：

前缀统计 \(\mathcal{OJ}\) \(acwing\)

\(\mathcal{No.}3\) 单调栈/单调队列：

例题：

直方图中最大的矩形 (单调栈) \(\mathcal{OJ}\) \(acwing\)

最大连续和 (单调队列) \(\mathcal{OJ}\)

\(\mathcal{No.}4\) 树状数组(\(\mathcal{Binary\ Indexed\ Tree\ /BIT}\))

例子：

实现：

\(\mathcal{Lowbit:}\)

修改:

结论： \(C\left[ 1\right]\ =\ \sum ^{i}_{(j=i-Lowbit(i) +1)}a[j]\)

查询:

完整代码如下:

例题:

树状数组 \(1\) ：单点修改，区间查询 \(\mathcal{OJ}\) \(luogu\)

二维树状数组 \(1\)：单点修改，区间查询 \(\mathcal{OJ}\)

树状数组 \(2\) ：区间修改，单点查询 \(OJ\) \(luogu\)

树状数组 \(3\) ：区间修改，区间查询 \(\mathcal{OJ}1\) \(\mathcal{OJ}2\) \(luogu\)

在区间修改单点查询的基础上,设原数组\(a[]\), 差分数组\(\mathcal{Tree[]}\)

于是,我们有 \(a[i] = \sum^i_{(j = 1)}\mathcal{Tree[j]}\)

进而, 我们有 \(\sum^n_{(i = 1)}a[i] = \sum^n_{(i = 1)}\sum^i_{(j = 1)}\mathcal{Tree[j]}\)

\(\Rightarrow \sum^n_{(i = 1)}a[i] = \sum^n_{(i = 1)}\mathcal{Tree[i]} * (n - i + 1)\)

\(∴ \sum^n_{(i = 1)}a[i] = \sum^n_{(i = 1)}\mathcal{Tree[i]} * n - \sum^n_{(i = 1)}\mathcal{Tree[i]} * (i - 1)\)

\(\mathcal{No.}5\) 分治\((\)二分，三分\()\)

例题：

\(\mathcal{Sumdiv}\) \(\mathcal{OJ}\) \(\mathcal{POJ}\)

设 \(n = \prod^m_{(i=1)}p^{a_i}_i\)， 因数和为\(\mathcal{Sum}\)

\(\mathcal{=>Sum}=\prod^m_{(i=1)}\sum^{a_i}_j p^j_i\)

而\(\sum^n_{\left(i = 1\right)} x^i= \Big\{^{\sum^{(n / 2)}_{(i = 1)} x^i *\ (x^{(n / 2)}\ +\ 1)\ \ (n\mod 2=0)}_{(\sum^{(n-1)}_{(i=1)}x^i)\ *\ x^n\ (n\mod2=1)}\)

曲线 \(\mathcal{OJ}\) \(\mathcal{luogu}\)

\(\mathcal{No.}6\ \ \mathcal{DP——}0/1\)背包

问题描述：

思路：

\(\mathcal{DP}(i,j)=\bigg\{^{\mathcal{DP}(i-1,j)\ (j\ <\ \mathcal{Volume_i})}_{\max(\mathcal{DP}(i-1,j),\ \mathcal{DP}(i-1,j-\mathcal{Volume_i})+Value_i)\ (j\geq\mathcal{Volume_i})}\)

\(\mathcal{DP}[i\&1][j]=\bigg\{^{\mathcal{DP}[(i - 1)\&1][j]\ (j < \mathcal{Volume_i})}_{\max(\mathcal{DP}[(i-1)\&1][j],\ \mathcal{DP}[(i-1)\&1][j-\mathcal{Volume_i}]+\mathcal{Value_i})\ (j\geq \mathcal{Volume_i})}\)

\(\mathcal{DP}[j]=\max(\mathcal{DP}[j]，\mathcal{DP}[j-\mathcal{Volume_i}] + \mathcal{Value_i})\)

例题：

选择卡片 \(\mathcal{OJ}\)

\(\mathcal{DP}[i][j]=\sum^{n}_{(k=i)}\mathcal{DP}[i-1][j-a[k]]\ (a[k]\leq j)\)

\(\mathcal{Sum}=\sum^{n}_{(i=1)}DP[i][i*Avg]\)

\(\mathcal{DP}[0][0]=1\)

\(\mathcal{No.}7\ \mathcal{DP}——\)完全背包

问题描述：

思路：

例题：

\(\mathcal{FATE}\) \(\mathcal{OJ}\) \(\mathcal{HDU}\)

\(\mathcal{DP}[i][j]=\max(\mathcal{DP}[i][j],\mathcal{DP}[i-1][j-b[k]]+a[k])\)

\(\mathcal{No.}8\) \(\mathcal{DFS}\)序\(/\)欧拉序\((\)重点\(\mathcal{DFS}\)序\()\)

定义：

作用

\(\mathcal{DFS}\)序\(:\)

欧拉序：

例题：

\(\mathcal{DFS}\)序\(1\) \(\mathcal{OJ}\) \(\mathcal{LOJ}\)

\(\mathcal{No.}9\) 树形\(\mathcal{DP}\)

就是在树形结构基础上的\(\mathcal{DP}\), 一般计算顺序为

根节点\(\Rightarrow\)叶节点 \(or\) 叶节点\(\Rightarrow\)根节点

一般实现框架

废话不多说，就在例题中领悟树形\(\mathcal{DP}\)的精髓吧

没有上司的舞会 \(\mathcal{OJ}1\) \(\mathcal{OJ}2\) \(\mathcal{OJ}3\) \(\mathcal{luogu}\) 重题好多

\(\mathcal{DP}[0][j]=\sum^{\mathcal{Tree[j].size()}-1}_{k=0}(\max(\mathcal{DP}[0][\mathcal{To}], \mathcal{DP}[1][\mathcal{To}])\ (\mathcal{To}=\mathcal{Tree}[j][k])\)

\(\mathcal{DP}[1][j]=\sum^{\mathcal{Tree[j].size()}-1}_{k=0}\mathcal{DP}[0][\mathcal{To}]\ (\mathcal{To}=\mathcal{Tree}[j][k])\)

初始化\(\mathcal{DP}[1][j]=a[j]\ (a\)为开心值\()\)，\(\mathcal{DP}[0][j]=0\)

选课 \(\mathcal{OJ}1\) \(\mathcal{OJ}2\) \(\mathcal{OJ}3\) \(\mathcal{OJ}4(\)略有不同\()\) \(\mathcal{luogu}\) 重题好多++

\(\mathcal{No.}10\) 区间\(\mathcal{DP}\)

定义:就是在区间上进行动态规划，求解一段区间上的最优解。主要是通过合并小区间的最优解进而得出整个大区间上最优解的\(\mathcal{DP}\)算法。类似分治

思路：

例题：

能量项链 \(\mathcal{OJ}1\) \(\mathcal{OJ}2\) \(\mathcal{OJ}3\) \(\mathcal{OJ}4\) \(\mathcal{luogu}\) \(\mathcal{LOJ}\) 重题好多++

设 \(n = \prod^m_{(i=1)}p^{a_i}_i\)，因数和为\(\mathcal{Sum}\)

而\(\sum^n_{\left(i = 1\right)} x^i= \Big\{^{\sum^{(n / 2)}_{(i = 1)} x^i \ (x^{(n / 2)}\ +\ 1)\ \ (n\mod 2=0)}_{(\sum^{(n-1)}_{(i=1)}x^i)\ \ x^n\ (n\mod2=1)}\)