一些有用的数学知识(Updating)
文章目录
拉格朗日插值公式
对于
n
−
1
n-1
n−1 次多项式
f
(
x
)
f(x)
f(x) 上的
n
n
n 个点
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
,
⋯
(
x
n
,
y
n
)
(x_1,y_1),(x_2,y_2),\cdots (x_n,y_n)
(x1,y1),(x2,y2),⋯(xn,yn) ,如果倒推出
f
(
x
)
f(x)
f(x) 的话,有
f
(
x
)
=
∑
i
=
1
n
y
i
∏
j
≠
i
x
−
x
j
x
i
−
x
j
f(x)=\sum_{i=1}^ny_i\prod_{j\not=i}\frac{x-x_j}{x_i-x_j}
f(x)=i=1∑nyij=i∏xi−xjx−xj
微分中值定理
费马引理
如果在一段曲线当中存在一个点
x
0
x_0
x0,使得在
x
0
x_0
x0 的邻域(包含
x
0
x_0
x0 的一段极小区间?)内都存在
f
(
x
)
≤
f
(
x
0
)
f(x)\leq f(x_0)
f(x)≤f(x0)(或
f
(
x
)
≥
f
(
x
0
)
f(x)\geq f(x_0)
f(x)≥f(x0)),那么
f
′
(
x
0
)
=
0
f'(x_0)=0
f′(x0)=0。
拉格朗日中值定理
若函数
f
(
x
)
f(x)
f(x) 满足
- 在闭区间
[
a
,
b
]
[a,b]
[a,b] 连续
- 在开区间
(
a
,
b
)
(a,b)
(a,b) 可导
那么存在
k
∈
(
a
,
b
)
k\in(a,b)
k∈(a,b) 满足:
f
′
(
k
)
=
f
(
b
)
−
f
(
a
)
b
−
a
f'(k)=\frac{f(b)-f(a)}{b-a}
f′(k)=b−af(b)−f(a)
柯西中值定理
对于两个函数
f
(
x
)
,
F
(
x
)
f(x),F(x)
f(x),F(x),若
- 都在闭区间
[
a
,
b
]
[a,b]
[a,b] 连续
- 都在开区间
(
a
,
b
)
(a,b)
(a,b) 可导
- 对于任意
x
∈
(
a
,
b
)
x\in(a,b)
x∈(a,b) ,
F
′
(
x
)
≠
0
F'(x)\not=0
F′(x)=0
那么存在
k
∈
(
a
,
b
)
k\in(a,b)
k∈(a,b) 满足
f
′
(
k
)
F
′
(
k
)
=
f
(
b
)
−
f
(
a
)
F
(
b
)
−
F
(
a
)
\frac{f'(k)}{F'(k)}=\frac{f(b)-f(a)}{F(b)-F(a)}
F′(k)f′(k)=F(b)−F(a)f(b)−f(a)
洛必达法则
对于两个函数
f
(
x
)
,
F
(
x
)
f(x),F(x)
f(x),F(x),若
- x
x
x 趋近于常数
a
a
a 时,
f
(
x
)
,
F
(
x
)
f(x),F(x)
f(x),F(x) 趋近于
0
0
0
- 在点
a
a
a 的去心领域内,两个函数可导,且
F
′
(
x
)
≠
0
F'(x)\not=0
F′(x)=0
- lim
x
→
0
f
′
(
x
)
F
′
(
x
)
\lim_{x\rightarrow0}\frac{f'(x)}{F'(x)}
limx→0F′(x)f′(x) 存在
那么
lim
x
→
a
f
(
x
)
F
(
x
)
=
lim
x
→
a
f
′
(
x
)
F
′
(
x
)
\lim_{x\rightarrow a}\frac{f(x)}{F(x)}=\lim_{x\rightarrow a}\frac{f'(x)}{F'(x)}
x→alimF(x)f(x)=x→alimF′(x)f′(x)
该公式可套娃
还有另一种变形,若
- x
x
x 趋近于
∞
\infty
∞ 时,
f
(
x
)
,
F
(
x
)
f(x),F(x)
f(x),F(x) 趋近于
0
0
0 或者
∞
\infty
∞
- 存在一个区间
(
−
∞
,
N
)
∪
(
N
,
+
∞
)
(-\infty,N)∪(N,+\infty)
(−∞,N)∪(N,+∞) 内,两个函数可导,且
F
′
(
x
)
≠
0
F'(x)\not=0
F′(x)=0
- lim
x
→
0
f
′
(
x
)
F
′
(
x
)
\lim_{x\rightarrow0}\frac{f'(x)}{F'(x)}
limx→0F′(x)f′(x) 存在
那么
lim
x
→
∞
f
(
x
)
F
(
x
)
=
lim
x
→
∞
f
′
(
x
)
F
′
(
x
)
\lim_{x\rightarrow \infty}\frac{f(x)}{F(x)}=\lim_{x\rightarrow \infty}\frac{f'(x)}{F'(x)}
x→∞limF(x)f(x)=x→∞limF′(x)f′(x)
连分数(NOI2021 D2T2 考点)
定义
对一个分数
p
q
\frac{p}{q}
qp 的分子分母
p
,
q
p,q
p,q 进行辗转相除法,令第
i
i
i 次除法得到的商为
a
i
−
1
a_{i-1}
ai−1,那么该分数就可以表示成连分数:
p
q
=
a
0
+
1
a
1
+
1
a
2
+
1
⋱
+
1
a
k
=
[
a
0
,
a
1
,
a
2
,
.
.
.
,
a
k
]
\cfrac pq=a_0+\cfrac{1}{a_1+\cfrac{1}{a_2+\cfrac{1}{\ddots+\cfrac{1}{a_k}}}}=[a_0,a_1,a_2,...,a_k]
qp=a0+a1+a2+⋱+ak1111=[a0,a1,a2,...,ak]
- 从
a
i
a_i
ai 算起到直到最后一项组成的连分数
[
a
i
,
a
i
+
1
,
.
.
.
,
a
k
]
[a_i,a_{i+1},...,a_k]
[ai,ai+1,...,ak] 称为该分数的第
i
i
i 个余项 / 余式,表示为
r
i
r_i
ri。因此,原分数可表示为
[
a
0
,
a
1
,
.
.
.
,
r
i
]
[a_0,a_1,...,r_i]
[a0,a1,...,ri],需要注意的是
r
i
r_i
ri 是个实数。
- 从第 0 项直到第
i
i
i 项组成的连分数
[
a
0
,
a
1
,
.
.
.
,
a
i
]
[a_0,a_1,...,a_i]
[a0,a1,...,ai] 称为第
i
i
i 近似 / 第
i
i
i 截断,表示为
s
i
s_i
si,写成分数形式的
s
i
=
p
i
q
i
s_i=\cfrac{p_i}{q_i}
si=qipi 则称为第
i
i
i 渐进分数 /
i
i
i 阶渐进分数。通过截取连分数的
i
i
i 阶渐进获取近似分数,能在分子分母尽量小的情况下,得到误差最小的结果。
- 无理数表示成连分数会有无穷项。
结论
定理1
对于一个实数
x
x
x 表示成连分数
[
a
0
,
a
1
,
a
2
,
.
.
.
]
[a_0,a_1,a_2,...]
[a0,a1,a2,...],令
s
k
=
p
k
q
k
s_k=\cfrac{p_k}{q_k}
sk=qkpk,则
{
p
0
=
a
0
q
0
=
1
,
{
p
1
=
a
0
a
1
+
1
q
1
=
a
1
,
{
p
k
=
a
k
p
k
−
1
+
p
k
−
2
q
k
=
a
k
q
k
−
1
+
q
k
−
2
{\bigg\lbrace}\begin{matrix}p_0=a_0\\q_0=1\end{matrix}\;,\; {\bigg\lbrace}\begin{matrix}p_1=a_0a_1+1\\q_1=a_1\end{matrix}\;,\; {\bigg\lbrace}\begin{matrix}p_k=a_kp_{k-1}+p_{k-2}\\q_k=a_kq_{k-1}+q_{k-2}\end{matrix}
{p0=a0q0=1,{p1=a0a1+1q1=a1,{pk=akpk−1+pk−2qk=akqk−1+qk−2
可以递推求渐进分数。而且,还保证了
g
c
d
(
p
k
,
q
k
)
=
1
{\rm gcd}(p_k,q_k)=1
gcd(pk,qk)=1 。
同时,可以发现
p
k
p_k
pk 和
q
k
q_k
qk 是递增的(除了
q
0
q_0
q0 可能等于
q
1
q_1
q1 以外)。当然,从连分数的性质出发来看,这是句废话。
定理2
把定理1里面的式子
p
k
=
a
k
p
k
−
1
+
p
k
−
2
p_k=a_kp_{k-1}+p_{k-2}
pk=akpk−1+pk−2
两边同除
p
k
−
1
p_{k-1}
pk−1,得
p
k
p
k
−
1
=
a
k
+
p
k
−
2
p
k
−
1
\cfrac{p_k}{p_{k-1}}=a_k+\cfrac{p_{k-2}}{p_{k-1}}
pk−1pk=ak+pk−1pk−2
按照这个规律迭代下去
p
k
p
k
−
1
=
a
k
+
1
p
k
−
1
p
k
−
2
=
a
k
+
1
a
k
−
1
+
p
k
−
3
p
k
−
2
=
a
k
+
1
a
k
−
1
+
1
a
k
−
2
+
1
⋱
+
a
0
=
[
a
k
,
a
k
−
1
,
.
.
.
,
a
0
]
\cfrac{p_k}{p_{k-1}}=a_k+\cfrac{1}{\cfrac{p_{k-1}}{p_{k-2}}}=a_k+\cfrac{1}{a_{k-1}+\cfrac{p_{k-3}}{p_{k-2}}}\\ =a_k+\cfrac{1}{a_{k-1}+\cfrac{1}{a_{k-2}+\cfrac{1}{\ddots+a_0}}}=[a_k,a_{k-1},...,a_0]
pk−1pk=ak+pk−2pk−11=ak+ak−1+pk−2pk−31=ak+ak−1+ak−2+⋱+a0111=[ak,ak−1,...,a0]
那么就可以得到一个很美观的推论:
p
k
p
k
−
1
=
[
a
k
,
a
k
−
1
,
.
.
.
,
a
0
]
(
a
0
≠
0
)
\cfrac{p_k}{p_{k-1}}=[a_k,a_{k-1},...,a_0]~~(a_0\not=0)
pk−1pk=[ak,ak−1,...,a0] (a0=0)
同理可得
q
k
q
k
−
1
=
[
a
k
,
a
k
−
1
,
.
.
.
,
a
1
]
\cfrac{q_k}{q_{k-1}}=[a_k,a_{k-1},...,a_1]
qk−1qk=[ak,ak−1,...,a1]
上述两个推论即定理2,又称反序定理。
定理3
为了凸显连分数的优越性,我们会对其相邻的渐进分数之差感兴趣,不妨求一求:
p
k
+
1
q
k
+
1
−
p
k
q
k
=
p
k
+
1
q
k
−
p
k
q
k
+
1
q
k
+
1
q
k
\cfrac{p_{k+1}}{q_{k+1}}-\cfrac{p_k}{q_k}=\cfrac{p_{k+1}q_k-p_kq_{k+1}}{q_{k+1}q_k}
qk+1pk+1−qkpk=qk+1qkpk+1qk−pkqk+1
两边同乘
q
k
+
1
q
k
q_{k+1}q_{k}
qk+1qk,可以有点思路,我们不妨先探究探究
p
k
+
1
q
k
−
p
k
q
k
+
1
p_{k+1}q_k-p_kq_{k+1}
pk+1qk−pkqk+1:
p
k
+
1
q
k
−
p
k
q
k
+
1
=
(
a
k
+
1
p
k
+
p
k
−
1
)
q
k
−
p
k
(
a
k
+
1
q
k
+
q
k
−
1
)
=
a
k
+
1
p
k
q
k
−
a
k
+
1
p
k
q
k
+
p
k
−
1
q
k
−
p
k
q
k
−
1
=
−
(
p
k
q
k
−
1
−
p
k
−
1
q
k
)
\begin{matrix} p_{k+1}q_k-p_kq_{k+1}&=&(a_{k+1}p_k+p_{k-1})q_k-p_k(a_{k+1}q_k+q_{k-1})\\ &=& a_{k+1}p_kq_k-a_{k+1}p_kq_k+p_{k-1}q_k-p_kq_{k-1}\\ &=& -(p_kq_{k-1}-p_{k-1}q_k) \end{matrix}
pk+1qk−pkqk+1===(ak+1pk+pk−1)qk−pk(ak+1qk+qk−1)ak+1pkqk−ak+1pkqk+pk−1qk−pkqk−1−(pkqk−1−pk−1qk)
右边相当于把左边的下标都减一,我们得到了一个递推式子。由于我们知道
p
1
q
0
−
p
0
q
1
=
a
0
a
1
+
1
−
a
0
a
1
=
1
p_1q_0-p_0q_1=a_0a_1+1-a_0a_1=1
p1q0−p0q1=a0a1+1−a0a1=1,因此,顺推过来,可以得到
p
k
+
1
q
k
−
p
k
q
k
+
1
=
(
−
1
)
k
p_{k+1}q_k-p_kq_{k+1}=(-1)^k
pk+1qk−pkqk+1=(−1)k
这便是定理3。
两边同除以分母积,可以得到很重要的推论,它回答了开头的问题:
p
k
+
1
q
k
+
1
−
p
k
q
k
=
(
−
1
)
k
q
k
+
1
q
k
\cfrac{p_{k+1}}{q_{k+1}}-\cfrac{p_k}{q_k}=\cfrac{(-1)^k}{q_{k+1}q_k}
qk+1pk+1−qkpk=qk+1qk(−1)k
定理4
通过定理3的推论,不难发现
- 定理4:对一个确定的连分数,其奇数项渐近分数严格递减,偶数项渐近分数严格递增,奇数项渐近分数总是大于相邻的偶数项渐近分数。
- 推论:任一奇数项渐近分数都大于任一偶数项渐近分数。
也可以通过下面的定理5严格证明。
定理5
到底第
i
i
i 阶渐进分数跟原数
x
x
x 相差多少呢?
我们可以先把
x
x
x 表示成带余项的连分数
[
a
0
,
a
1
,
.
.
.
,
a
i
,
r
i
+
1
]
[a_0,a_1,...,a_i,r_{i+1}]
[a0,a1,...,ai,ri+1] ,此时第
i
+
1
i+1
i+1 阶渐进分数就等于
x
x
x,通过定理3的推论,我们可以直接得出定理5:
x
−
p
i
q
i
=
(
−
1
)
i
q
i
q
i
+
1
=
(
−
1
)
i
q
i
(
r
i
+
1
q
i
+
q
i
−
1
)
x-\cfrac{p_i}{q_i}=\cfrac{(-1)^i}{q_iq_{i+1}}=\cfrac{(-1)^i}{q_i(r_{i+1}q_i+q_{i-1})}
x−qipi=qiqi+1(−1)i=qi(ri+1qi+qi−1)(−1)i
也就是说,除了最后一项渐进分数以外(没有
r
i
+
1
r_{i+1}
ri+1),奇数阶渐进分数恒大于
x
x
x ,偶数阶渐进分数恒小于
x
x
x 。
此时注意到,笔者专门在定理1结尾强调了
p
k
p_k
pk 和
q
k
q_k
qk 的单调递增性。这样综合定理5就可以证明定理4及其推论了。同时,我们可以得到
i
i
i 阶渐进分数的大致图像了。
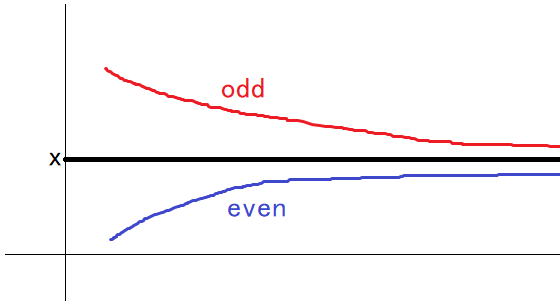
欧拉公式
e
i
x
=
cos
x
+
i
sin
x
e^{ix}=\cos x+i\sin x
eix=cosx+isinx
正余弦的展开
由于
sin
′
x
=
cos
x
cos
′
x
=
−
sin
x
\sin'x=\cos x\\ \cos'x=-\sin x
sin′x=cosxcos′x=−sinx
所以,对它们进行泰勒展开,用麦克劳林公式,可以得到:
sin
x
=
sin
0
+
sin
′
0
1
!
x
+
sin
′
′
0
2
!
x
2
+
.
.
.
=
x
−
x
3
3
!
+
x
5
5
!
−
x
7
7
!
+
.
.
.
cos
x
=
cos
0
+
cos
′
0
1
!
x
+
cos
′
′
0
2
!
x
2
+
.
.
.
=
1
−
x
2
2
!
+
x
4
4
!
−
x
6
6
!
+
.
.
.
\sin x=\sin0+\frac{\sin'0}{1!}x+\frac{\sin''0}{2!}x^2+...=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+...\\ \cos x=\cos0+\frac{\cos'0}{1!}x+\frac{\cos''0}{2!}x^2+...=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+...
sinx=sin0+1!sin′0x+2!sin′′0x2+...=x−3!x3+5!x5−7!x7+...cosx=cos0+1!cos′0x+2!cos′′0x2+...=1−2!x2+4!x4−6!x6+...
虚数单位
虚数单位
i
i
i 有很多美妙的性质,其中一个就是它的整数次幂:
i
4
n
=
1
i
4
n
+
1
=
i
i
4
n
+
2
=
−
1
i
4
n
+
3
=
−
i
i^{4n}=1\\ i^{4n+1}=i\\ i^{4n+2}=-1\\ i^{4n+3}=-i
i4n=1i4n+1=ii4n+2=−1i4n+3=−i
把虚数单位加入进正余弦的展开中,刚好可以去除正负号,便于下一步推导:
sin
x
=
i
x
+
(
i
x
)
3
3
!
+
(
i
x
)
5
5
!
+
(
i
x
)
7
7
!
+
.
.
.
i
cos
x
=
(
i
x
)
0
+
(
i
x
)
2
2
!
+
(
i
x
)
4
4
!
+
(
i
x
)
6
6
!
+
.
.
.
\sin x=\cfrac{ix+\cfrac{(ix)^3}{3!}+\cfrac{(ix)^5}{5!}+\cfrac{(ix)^7}{7!}+...}{i}\\ \cos x=(ix)^0+\cfrac{(ix)^2}{2!}+\cfrac{(ix)^4}{4!}+\cfrac{(ix)^6}{6!}+...
sinx=iix+3!(ix)3+5!(ix)5+7!(ix)7+...cosx=(ix)0+2!(ix)2+4!(ix)4+6!(ix)6+...
整合
先把正弦的大横线去除掉:
i
sin
x
=
i
x
+
(
i
x
)
3
3
!
+
(
i
x
)
5
5
!
+
(
i
x
)
7
7
!
+
.
.
.
i\sin x=ix+\cfrac{(ix)^3}{3!}+\cfrac{(ix)^5}{5!}+\cfrac{(ix)^7}{7!}+...
isinx=ix+3!(ix)3+5!(ix)5+7!(ix)7+...
接下来就很明朗了:
cos
x
+
i
sin
x
=
1
+
i
x
1
!
+
(
i
x
)
2
2
!
+
(
i
x
)
3
3
!
+
.
.
.
\cos x+i\sin x=1+\cfrac{ix}{1!}+\cfrac{(ix)^2}{2!}+\cfrac{(ix)^3}{3!}+...
cosx+isinx=1+1!ix+2!(ix)2+3!(ix)3+...
刚好是
e
i
x
e^{ix}
eix 的麦克劳林展开。
逆代
倒着用这个公式,可以得到三角函数的另一种表达式:
sin
x
=
e
i
x
−
e
−
i
x
2
i
=
(
exp
(
i
x
)
−
exp
(
−
i
x
)
)
⋅
(
2
i
)
−
1
cos
x
=
e
i
x
+
e
−
i
x
2
=
(
exp
(
i
x
)
+
exp
(
−
i
x
)
)
⋅
2
−
1
\sin x=\cfrac{e^{ix}-e^{-ix}}{2i}=(\exp(ix)-\exp(-ix))\cdot(2i)^{-1}\\ \cos x=\cfrac{e^{ix}+e^{-ix}}{2}=(\exp(ix)+\exp(-ix))\cdot2^{-1}
sinx=2ieix−e−ix=(exp(ix)−exp(−ix))⋅(2i)−1cosx=2eix+e−ix=(exp(ix)+exp(−ix))⋅2−1
最右边的表达式是可以直接运用到多项式三角函数中的。
Binet-Cauchy 公式
设矩阵
A
=
(
a
i
,
j
)
s
×
n
,
B
=
(
b
i
,
j
)
n
×
s
A=(a_{i,j})_{s\times n}~,~B=(b_{i,j})_{n\times s}
A=(ai,j)s×n , B=(bi,j)n×s ,则
- s
>
n
s>n
s>n:
∣
A
B
∣
=
0
|AB|=0
∣AB∣=0.
- s
≤
n
s\leq n
s≤n:
∣
A
B
∣
=
|AB|=
∣AB∣=
∑
1
≤
i
1
<
i
2
<
.
.
.
<
i
s
≤
n
∣
a
1
,
i
1
a
1
,
i
2
.
.
.
a
1
,
i
s
a
2
,
i
1
a
2
,
i
2
.
.
.
a
2
,
i
s
.
.
.
.
.
.
⋱
.
.
.
a
s
,
i
1
a
s
,
i
2
.
.
.
a
s
,
i
s
∣
⋅
∣
b
i
1
,
1
b
i
1
,
2
.
.
.
b
i
1
,
s
b
i
2
,
1
b
i
2
,
2
.
.
.
b
i
2
,
s
.
.
.
.
.
.
⋱
.
.
.
b
i
s
,
1
b
i
s
,
2
.
.
.
b
i
s
,
s
∣
\sum_{1\leq i_1<i_2<...<i_s\leq n} \left|\begin{matrix} a_{1,i_1}&a_{1,i_2}&...&a_{1,i_s}\\ a_{2,i_1}&a_{2,i_2}&...&a_{2,i_s}\\ ...&...&_\ddots&...\\ a_{s,i_1}&a_{s,i_2}&...&a_{s,i_s} \end{matrix}\right|\cdot \left|\begin{matrix} b_{i_1,1}&b_{i_1,2}&...&b_{i_1,s}\\ b_{i_2,1}&b_{i_2,2}&...&b_{i_2,s}\\ ...&...&_\ddots&...\\ b_{i_s,1}&b_{i_s,2}&...&b_{i_s,s}\\ \end{matrix}\right|
1≤i1<i2<...<is≤n∑∣∣∣∣∣∣∣∣a1,i1a2,i1...as,i1a1,i2a2,i2...as,i2......⋱...a1,isa2,is...as,is∣∣∣∣∣∣∣∣⋅∣∣∣∣∣∣∣∣bi1,1bi2,1...bis,1bi1,2bi2,2...bis,2......⋱...bi1,sbi2,s...bis,s∣∣∣∣∣∣∣∣
[朝花夕拾] 柯西不等式
对不起,球哥,我又把柯西忘了。
我这就复习……
二维形式
梦开始的地方:
∑
i
=
1
n
a
i
2
∑
i
=
1
n
b
i
2
≥
C
a
u
c
h
y
(
∑
i
=
1
n
a
i
b
i
)
2
\sum_{i=1}^{n}a_i^2\sum_{i=1}^{n}b_i^2\overset{Cauchy}{\geq}\left(\sum_{i=1}^{n}a_ib_i\right)^2
i=1∑nai2i=1∑nbi2≥Cauchy(i=1∑naibi)2
即 平方 和 的 积 大于等于 积 和 的 平方,左右刚好回文。
取等条件是对于
b
i
≠
0
b_i\not=0
bi=0 的所有
i
i
i ,满足
a
i
b
i
\frac{a_i}{b_i}
biai 都相等,同时对于
b
i
=
0
b_i=0
bi=0 的
i
i
i ,满足
a
i
=
0
a_i=0
ai=0。
向量形式
又是一个如此美妙的不等式:
A
→
=
(
a
1
,
a
2
,
.
.
.
,
a
n
)
,
B
→
=
(
b
1
,
b
2
,
.
.
.
,
b
n
)
∣
A
→
∣
⋅
∣
B
→
∣
≥
∣
A
→
⋅
B
→
∣
\overset{\rightarrow}{A}=(a_1,a_2,...,a_n)~,~\overset{\rightarrow}{B}=(b_1,b_2,...,b_n)\\ \left|\overset{\rightarrow}{A}\right|\cdot \left|\overset{\rightarrow}{B}\right|\geq \left|\overset{\rightarrow}{A}\cdot\overset{\rightarrow}{B}\right|
A→=(a1,a2,...,an) , B→=(b1,b2,...,bn)∣∣∣A→∣∣∣⋅∣∣∣B→∣∣∣≥∣∣∣A→⋅B→∣∣∣
这个是关于向量的一个基本不等式,很好证,只需要根据向量内积定义展开,当且仅当两向量共线时取等。
实际上,这个就是柯西不等式:
∣
A
→
∣
⋅
∣
B
→
∣
=
∣
(
a
1
,
a
2
,
.
.
.
,
a
n
)
∣
⋅
∣
(
b
1
,
b
2
,
.
.
.
,
b
n
)
∣
=
∑
i
=
1
n
a
i
2
⋅
∑
i
=
1
n
b
i
2
≥
∣
A
→
⋅
B
→
∣
=
∣
(
a
1
,
a
2
,
.
.
.
,
a
n
)
⋅
(
b
1
,
b
2
,
.
.
.
,
b
n
)
∣
=
∣
∑
i
=
1
n
a
i
b
i
∣
\left|\overset{\rightarrow}{A}\right|\cdot \left|\overset{\rightarrow}{B}\right|=|(a_1,a_2,...,a_n)|\cdot |(b_1,b_2,...,b_n)|=\sqrt{\sum_{i=1}^{n}a_i^2}\cdot\sqrt{\sum_{i=1}^{n}b_i^2}\\ \geq \left|\overset{\rightarrow}{A}\cdot\overset{\rightarrow}{B}\right|=\Big|(a_1,a_2,...,a_n)\cdot (b_1,b_2,...,b_n)\Big|=\left|\sum_{i=1}^{n}a_ib_i\right|
∣∣∣A→∣∣∣⋅∣∣∣B→∣∣∣=∣(a1,a2,...,an)∣⋅∣(b1,b2,...,bn)∣=i=1∑nai2
⋅i=1∑nbi2
≥∣∣∣A→⋅B→∣∣∣=∣∣∣(a1,a2,...,an)⋅(b1,b2,...,bn)∣∣∣=∣∣∣∣∣i=1∑naibi∣∣∣∣∣
把两边平方就可以得到二维形式。
同时,二维形式的取等条件刚好等价于向量
(
a
1
,
a
2
,
.
.
.
,
a
n
)
(a_1,a_2,...,a_n)
(a1,a2,...,an) 与向量
(
b
1
,
b
2
,
.
.
.
,
b
n
)
(b_1,b_2,...,b_n)
(b1,b2,...,bn) 共线。
所以,向量形式不失为一种很好的证明柯西不等式的方法。
期望形式
这个不等式就有点意思了
E
(
X
2
)
⋅
E
(
Y
2
)
≥
∣
E
(
X
Y
)
∣
⇒
E
(
X
2
)
E
(
Y
2
)
≥
(
E
(
X
Y
)
)
2
\sqrt{E(X^2)}\cdot\sqrt{E(Y^2)}\geq |E(XY)|\\ \Rightarrow E(X^2)E(Y^2)\geq \big(E(XY)\big)^2
E(X2)
⋅E(Y2)
≥∣E(XY)∣⇒E(X2)E(Y2)≥(E(XY))2
证明过程非常不一样,与传统柯西不等式并没扯上关联。
定义一个二次函数:
y
=
E
(
X
2
)
t
2
+
2
E
(
X
Y
)
t
+
E
(
Y
2
)
y=E(X^2)t^2+2E(XY)t+E(Y^2)
y=E(X2)t2+2E(XY)t+E(Y2) ,不难发现
y
=
E
(
X
2
t
2
)
+
E
(
2
X
Y
t
)
+
E
(
Y
2
)
=
E
(
(
X
t
)
2
+
2
(
X
t
)
Y
+
Y
2
)
=
E
(
(
X
t
+
Y
)
2
)
≥
0
y=E(X^2t^2)+E(2XYt)+E(Y^2)=E\big((Xt)^2+2(Xt)Y+Y^2\big)\\ =E\left(\big(Xt+Y\big)^2\right)\geq0
y=E(X2t2)+E(2XYt)+E(Y2)=E((Xt)2+2(Xt)Y+Y2)=E((Xt+Y)2)≥0
一个二次函数大于等于 0 ,说明
Δ
≤
0
\Delta\leq0
Δ≤0 ,而
Δ
=
(
2
E
(
X
Y
)
)
2
−
4
⋅
E
(
X
2
)
E
(
Y
2
)
\Delta=\big(2E(XY)\big)^2-4\cdot E(X^2)E(Y^2)
Δ=(2E(XY))2−4⋅E(X2)E(Y2)
所以
4
(
E
(
X
Y
)
)
2
−
4
⋅
E
(
X
2
)
E
(
Y
2
)
≤
0
⇒
E
(
X
2
)
E
(
Y
2
)
≥
(
E
(
X
Y
)
)
2
4\big(E(XY)\big)^2-4\cdot E(X^2)E(Y^2)\leq0\\ \Rightarrow E(X^2)E(Y^2)\geq\big(E(XY)\big)^2
4(E(XY))2−4⋅E(X2)E(Y2)≤0⇒E(X2)E(Y2)≥(E(XY))2
至于取等条件,有些玄学。根据式子,取等时
(
X
t
+
Y
)
=
0
(Xt+Y)=0
(Xt+Y)=0 ,也就是
X
,
Y
X,Y
X,Y 要成固定常数倍关系(或其中一方为 0)。其中一个为 0 可以理解,因为
Y
Y
Y 取 0 时对方不论取什么都存在
t
=
0
t=0
t=0 使之成立。但是倍数关系,真的可能吗?
X
,
Y
X,Y
X,Y 都是随机变量,两个都随机取,一个刚好是另一个的
λ
\lambda
λ 倍的概率并不是
100
%
\tt100\%
100% 吧?
看来,要么是
X
,
Y
X,Y
X,Y 并不彼此独立,要么是我见识浅了。
积分形式
(
∫
f
2
(
x
)
d
x
)
⋅
(
∫
g
2
(
x
)
d
x
)
≥
(
∫
f
(
x
)
g
(
x
)
d
x
)
2
\left(\int f^2(x)dx\right)\cdot\left(\int g^2(x)dx\right)\geq\left(\int f(x)g(x)dx\right)^2
(∫f2(x)dx)⋅(∫g2(x)dx)≥(∫f(x)g(x)dx)2
其实,用微元法,可以发现它就是柯西不等式的二维展开形式。
当然,也可以用期望形式一样的方法,用构造二次函数去证明。
既然本质就是二位展开形式,那么取等条件就是
f
(
x
)
f(x)
f(x) 和
g
(
x
)
g(x)
g(x) 线性相关了,也就是有
∀
x
,
f
(
x
)
=
λ
g
(
x
)
\forall x,f(x)=\lambda g(x)
∀x,f(x)=λg(x) 或
∀
x
,
g
(
x
)
=
λ
f
(
x
)
\forall x,g(x)=\lambda f(x)
∀x,g(x)=λf(x) 成立。
数论结论
缩系元素求积
令
N
N
N 的缩系为
S
S
S ,求
∏
x
∈
S
x
m
o
d
N
\prod_{x\in S} x\mod N
∏x∈SxmodN ,或者说
∏
x
<
N
x
[
g
c
d
(
x
,
N
)
=
1
]
m
o
d
N
\prod_{x<N}x^{[gcd(x,N)=1]}\mod N
x<N∏x[gcd(x,N)=1]modN
分情况讨论:
如果
N
N
N 有原根,取一个原根为
g
g
g ,由原根的定义,以及原根存在逆元,可以得出
S
=
{
g
i
∣
1
≤
i
≤
φ
(
N
)
}
S=\{g^i|1\leq i\leqφ(N)\}
S={gi∣1≤i≤φ(N)} ,那么原式就等于
∏
i
=
1
φ
(
N
)
g
i
≡
g
(
φ
(
N
)
+
1
)
φ
(
N
)
2
≡
(
g
φ
(
N
)
+
1
)
φ
(
N
)
2
≡
g
φ
(
N
)
2
\prod_{i=1}^{φ(N)} g^i\equiv g^{\frac{(φ(N)+1)φ(N)}{2}}\equiv \left(g^{φ(N)+1}\right)^{\frac{φ(N)}{2}}\equiv g^{\frac{φ(N)}{2}}
i=1∏φ(N)gi≡g2(φ(N)+1)φ(N)≡(gφ(N)+1)2φ(N)≡g2φ(N)
由于
g
φ
(
N
)
≡
1
g^{φ(N)}\equiv1
gφ(N)≡1 ,且
g
g
g 是原根,所以
g
φ
(
N
)
2
g^{\frac{φ(N)}{2}}
g2φ(N) 不可能为 1,只能为 -1。故对于
N
N
N 存在原根的情况,
∏
x
∈
S
x
≡
−
1
(
m
o
d
N
)
\prod_{x\in S}x\equiv -1~~~({\rm mod}~N)
x∈S∏x≡−1 (mod N)
如果
N
N
N 无原根怎么办?首先解决
N
=
2
k
N=2^k
N=2k 的问题。
1
,
2
,
4
1,2,4
1,2,4 都有原根,不必说了。当
N
≥
8
N\geq8
N≥8 时,
∏
x
<
N
x
[
g
c
d
(
x
,
N
)
=
1
]
≡
1
∗
3
∗
5
∗
.
.
.
∗
(
N
−
1
)
≡
∏
x
<
N
/
2
x
[
g
c
d
(
x
,
N
/
2
)
=
1
]
∏
x
<
N
/
2
(
−
x
)
[
g
c
d
(
x
,
N
/
2
)
=
1
]
≡
(
∏
x
<
N
/
2
x
[
g
c
d
(
x
,
N
/
2
)
=
1
]
)
2
⋅
(
−
1
)
φ
(
N
/
2
)
\prod_{x<N}x^{[gcd(x,N)=1]}\equiv1*3*5*...*(N-1)\equiv \prod_{x<N/2}x^{[gcd(x,N/2)=1]}\prod_{x<N/2}(-x)^{[gcd(x,N/2)=1]}\\ \equiv (\prod_{x<N/2}x^{[gcd(x,N/2)=1]})^2\cdot (-1)^{φ(N/2)}
x<N∏x[gcd(x,N)=1]≡1∗3∗5∗...∗(N−1)≡x<N/2∏x[gcd(x,N/2)=1]x<N/2∏(−x)[gcd(x,N/2)=1]≡(x<N/2∏x[gcd(x,N/2)=1])2⋅(−1)φ(N/2)
于是,我们可以从
N
=
4
N=4
N=4 的情况一直递推过来,由于
φ
(
N
)
φ(N)
φ(N) 除了 2 以外都是偶数,因此我们得出:
∏
x
∈
S
x
≡
1
(
m
o
d
N
=
2
k
≥
8
)
\prod_{x\in S}x\equiv 1~~~({\rm mod}~N=2^k\geq8)
x∈S∏x≡1 (mod N=2k≥8)
对于
N
≠
2
k
N\not=2^k
N=2k 的情况,我们进行质因数分解。
令
N
=
p
1
w
1
p
2
w
2
.
.
.
p
k
w
k
N=p_1^{w_1}p_2^{w_2}...p_k^{w_k}
N=p1w1p2w2...pkwk ,不妨设
x
i
=
p
i
w
i
x_i=p_i^{w_i}
xi=piwi。
我们知道
φ
(
N
)
=
∏
φ
(
x
i
)
φ(N)=\prodφ(x_i)
φ(N)=∏φ(xi) ,因此根据缩系的性质,把
N
N
N 的缩系
S
S
S 取模
x
i
x_i
xi 后变为可重集,就相当于
x
i
x_i
xi 的缩系中每个元素重复
φ
(
N
)
φ
(
x
i
)
\frac{φ(N)}{φ(x_i)}
φ(xi)φ(N) 次。
设
F
(
N
)
=
∏
x
<
N
x
[
g
c
d
(
x
,
N
)
=
1
]
m
o
d
N
F(N)=\prod_{x<N}x^{[gcd(x,N)=1]}\mod N
F(N)=∏x<Nx[gcd(x,N)=1]modN ,那么
{
F
(
N
)
≡
F
(
x
1
)
φ
(
N
)
φ
(
x
1
)
m
o
d
x
1
F
(
N
)
≡
F
(
x
2
)
φ
(
N
)
φ
(
x
2
)
m
o
d
x
2
…
F
(
N
)
≡
F
(
x
k
)
φ
(
N
)
φ
(
x
k
)
m
o
d
x
k
\begin{cases} F(N)\equiv F(x_1)^{\frac{φ(N)}{φ(x_1)}}~~\mod x_1\\ F(N)\equiv F(x_2)^{\frac{φ(N)}{φ(x_2)}}~~\mod x_2\\ \ldots\\ F(N)\equiv F(x_k)^{\frac{φ(N)}{φ(x_k)}}~~\mod x_k\\ \end{cases}
⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧F(N)≡F(x1)φ(x1)φ(N) modx1F(N)≡F(x2)φ(x2)φ(N) modx2…F(N)≡F(xk)φ(xk)φ(N) modxk
由于
x
i
x_i
xi 要么是
2
k
2^k
2k ,要么有原根,因此
F
(
x
i
)
2
=
1
F(x_i)^2=1
F(xi)2=1 ,再根据
φ
φ
φ 的奇偶性(
N
N
N 不为
2
p
2p
2p, 所以
φ
(
N
)
φ
(
x
i
)
\frac{φ(N)}{φ(x_i)}
φ(xi)φ(N) 都是偶数),不难得出上面的线性同余方程其实就是
{
F
(
N
)
≡
1
m
o
d
x
1
F
(
N
)
≡
1
m
o
d
x
2
…
F
(
N
)
≡
1
m
o
d
x
k
\begin{cases} F(N)\equiv 1~~\mod x_1\\ F(N)\equiv 1~~\mod x_2\\ \ldots\\ F(N)\equiv 1~~\mod x_k\\ \end{cases}
⎩⎪⎪⎪⎨⎪⎪⎪⎧F(N)≡1 modx1F(N)≡1 modx2…F(N)≡1 modxk
用中国剩余定理合并起来,会得到
F
(
N
)
=
1
F(N)=1
F(N)=1 的结论。
综上,
∏
x
<
N
x
[
g
c
d
(
x
,
N
)
=
1
]
m
o
d
N
\prod_{x<N}x^{[gcd(x,N)=1]}\mod N
∏x<Nx[gcd(x,N)=1]modN 在
N
N
N 有原根时同余于 -1 ,否则为 1 。
因数闭合序列矩阵
若一个正整数集合中每个数的所有因数都同在这个集合里,那么称这个集合是因数闭合的。
把这个集合中的元素从小到大放入序列
a
a
a ,序列大小为
n
n
n。
在
n
×
n
n\times n
n×n 的矩阵
A
A
A 中,
A
i
,
j
=
g
c
d
(
a
i
,
a
j
)
A_{i,j}={\rm gcd}(a_i,a_j)
Ai,j=gcd(ai,aj)。
那么
d
e
t
(
A
)
{\rm det}(A)
det(A) 等于多少呢?
用构造矩阵的方法求这个行列式。我们构造两个
n
×
n
n\times n
n×n 的矩阵:
G
i
,
j
=
{
ϕ
(
a
j
)
,
a
j
∣
a
i
0
,
a
j
∤
a
i
H
i
,
j
=
{
1
,
a
i
∣
a
j
0
,
a
i
∤
a
j
G_{i,j}= \begin{cases} {\rm \phi}(a_j) ,& a_j|a_i\\ 0,& a_j\!\!\!\not|a_i \end{cases}\\ H_{i,j}= \begin{cases} 1 ,& a_i|a_j\\ 0,& a_i\!\!\!\not|a_j \end{cases}
Gi,j={ϕ(aj),0,aj∣aiaj∣aiHi,j={1,0,ai∣ajai∣aj
那么两矩阵的乘积:
∑
k
=
1
n
G
i
,
k
⋅
H
k
,
j
=
∑
k
=
1
n
ϕ
(
a
k
)
[
a
k
∣
a
i
]
[
a
k
∣
a
j
]
=
∑
a
k
∣
g
c
d
(
a
i
,
a
j
)
ϕ
(
a
k
)
=
g
c
d
(
a
i
,
a
j
)
=
A
i
,
j
\sum_{k=1}^{n}G_{i,k}\cdot H_{k,j}=\sum_{k=1}^{n}\phi(a_k)[a_k|a_i][a_k|a_j]=\sum_{a_k|{\rm gcd}(a_i,a_j)}\phi(a_k)={\rm gcd}(a_i,a_j)=A_{i,j}
k=1∑nGi,k⋅Hk,j=k=1∑nϕ(ak)[ak∣ai][ak∣aj]=ak∣gcd(ai,aj)∑ϕ(ak)=gcd(ai,aj)=Ai,j
可得
A
=
G
⋅
H
A=G\cdot H
A=G⋅H
不难发现,
G
G
G 和
H
H
H 都是下三角矩阵,因此
det
(
A
)
=
det
(
G
)
⋅
det
(
H
)
=
∏
i
=
1
n
ϕ
(
a
i
)
\det(A)=\det(G)\cdot\det(H)=\prod_{i=1}^{n}\phi(a_i)
det(A)=det(G)⋅det(H)=i=1∏nϕ(ai)
最新文章
- delphi xe4 程序添加管理员权限要求后不能调试的解决方法
- java 文件按行读取
- plink远程连接服务器进行编译
- Glow Android 优化实践
- NOIP欢乐模拟赛 T2 解题报告
- redis配置文件解析
- 《JavaScript设计模式与开发实践》读书笔记之享元模式
- git clone分支
- SSM(Maven集成)
- Android Google AdMob 广告接入示例
- mvc部分视图转换成html字符串
- redis设置密码
- Mac redis安装
- Java和Android的Lru缓存,及其实现原理
- Solution for unable to create "dead-letter-exchange" in RabbitMQ
- eclipse 里,打开的文件的各个标签,标题乱码。
- HPU 1476: 括号括号
- 常用CSS实例
- 20145324 Java实验三
- Autodesk FBX SDK Program 中文 (一)
热门文章
- WIN32 API 获取文件版本信息
- flowable与camunda性能测试对比分析
- 开发工具-在线计算MD5
- Ubuntu Linux处理Waiting for cache lock: Could not get lock /var/lib/dpkg/lock-frontend. It is held by process 3365 (unattended-upgr)问题
- idea中一些常用的快捷键
- .Net Core 中使用工厂模式
- 一图读懂k8s informer client-go
- java中常见的锁
- 华为Mate14上安装Ubuntu20.04纪要
- linux 文件名乱码的文件无法删除