建堆复杂度O(n)证明

堆排序中首先需要做的就是建堆，广为人知的是建堆复杂度才O(n)，它的证明过程涉及到高等数学中的级数或者概率论，不过证明整体来讲是比较易懂的。

堆排过程

代码如下

void print(vector<int> &arr)

{

    for(auto n: arr) printf("%d\t", n);

    cout<<endl;

}

// 以arr[n]为根的子树，将arr[n]向下调整至合适位置

void Heapify(vector<int> &arr, int size, int n)

{

    int L = n*2+1, R = L+1;

    if(L>=size) return ;//无孩

    int big = arr[L];         // 取两孩之大者

    if(R<size) big = max(big, arr[R]);

    if(arr[n]>=big) return ;  //无需调整

    int c = L;      // 欲与父交换位置的孩子

    if(big!=arr[L]) c = R;

    swap(arr[n], arr[c]);

    Heapify(arr, size, c);

}

// 小根堆

void BuildHeap(vector<int> &arr)

{

    int last = (arr.size()-1)/2;

    for(int i=last; i>=0; i--) {

        Heapify(arr, arr.size(), i);

    }

}

// 顺便排序

void Sort(vector<int> &arr)

{

    int size = arr.size();

    for(int i=size-1; i>0; i--) {

        swap(arr[0], arr[i]);

        Heapify(arr, i, 0); //调整一下arr[0]

    }

}

int main()

{

    vector<int> vect{9, 10, 6, 3, 1, 6, 2, 8, 4};

    print(vect); //排序前

    BuildHeap(vect); //建堆

    Sort(vect);  //排序

    print(vect); //排序后

    return 0;

}

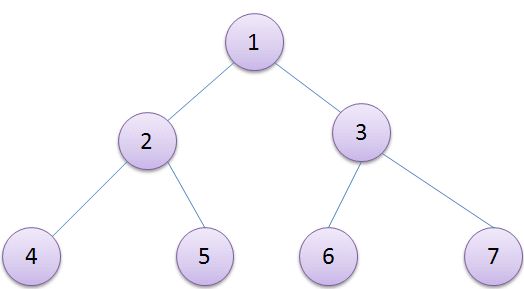
建堆的过程就是从最后一个分支结点开始逐层向上遍历，将结点向下调整至合适的位置，以不至于破坏原来的堆。比如上图，遍历的结点编号依次为3 2 1，首先调整以3为根的子树成堆，其次是以2为根的子树成堆，最后是以1为根的子树成堆。至此建堆完成，复杂度O(n)。

注意：建堆不能写成如下这样，这样的建堆算法复杂度是O(nlogn)，虽然不会影响堆排序的复杂度O(nlogn)，但是实现其他算法时就很不利了。

// 将arr[n]向上调整至合适位置

void AdjustHeap(vector<int> &arr, int n)

{

    if(n<=0) return ;

    if(arr[(n-1)/2] > arr[n]) {  //与父结点比较

        swap(arr[(n-1)/2], arr[n]);

        AdjustHeap(arr, (n-1)/2);   //递归调整

    }

}

// 小根堆

void BuildHeap(vector<int> &arr)

{

    for(int i=1; i<arr.size(); i++) {

        AdjustHeap(arr, i);

    }

}

复杂度计算

从直观上看，Heapify()的递归深度最多为\({log_n}\)，故它的复杂度上限为O(logn)。而BuildHeap()中的循环为\({ \frac{n}{2} }\)次，故它的复杂度为O(nlogn)，但这不是它的实际复杂度，而是一个估算的上界，它很可能永远达不到这个上界。为了方便计算，考虑结点数量为n，高度为h的满二叉树，因此\({2^h-1 = n}\)，即\({h = log_2{(n+1)}}\)。

第几层	最多调整次数	层调整次数累计
\({h}\)	\(0\)	\({2^{h-1}*0}\)
\({h-1}\)	\(1\)	\({2^{h-2}*1}\)
\({h-2}\)	\(2\)	\({2^{h-3}*2}\)
\(\vdots\)	\(\vdots\)	\(\vdots\)
\(3\)	\({ h-3 }\)	\({2^{2}*(h-3)}\)
\(2\)	\({ h-2 }\)	\({2^{1}*(h-2)}\)
\(1\)	\({ h-1 }\)	\({2^{0}*(h-1)}\)

将最右边一列累加起来就是建堆的调整次数，则建堆的调整次数\({S(n)}\)为

\[{S(n) = 1*2^{h-2}+2*2^{h-3}+}\cdots {+(h-2)*2^1 +(h-1)*2^0}
\]

\[{=2^{h-1} * ( \frac{1}{2^{1}} +\frac{2}{2^{2}} +\frac{3}{2^{3}} +}\cdots {+\frac{h-2}{2^{h-2}} +\frac{h-1}{2^{h-1}} )} \tag{1}
\]

则

\[{\frac{1}{2} S(n) = 2^{h-1} *(\frac{1}{2^2} + \frac{2}{2^3} + \frac{3}{2^4} + }\cdots{+\frac{h-2}{2^{h-1}} +\frac{h-1}{2^h})} \tag{2}
\]

将(1)式减去(2)式得

\[{S(n)-\frac{1}{2}S(n) = 2^{h-1} * (\frac{1}{2^1} + \frac{1}{2^2} + \frac{1}{2^3} + }\cdots{+\frac{1}{2^{h-2}} + \frac{1}{2^{h-1}} -\frac{h-1}{2^h} )}
\]

\[{ = 2^{h-1} * (\frac{1}{1-\frac{1}{2}}-1-\frac{h-1}{2^h} ) } \tag{3}
\]

\[{ =2^{h-1} * ( 1 - \frac{h-1}{2^h})}
\]

\[{ =2^{h-1}}
\]

又因 \({ n = 2^h-1 }\)，故有

\[{S(n) = 2^h = \frac{n+1}{2}}
\]

注意：上面列式均是当n趋于无穷大时的计算，且(3)式是由级数的直接变换所得。其他的证明思路还有用概率的，就不写了。

写公式写到头皮发麻，写错n次了，如果错漏请不吝指正，感谢！

巴特西

建堆复杂度O(n)证明

堆排过程

复杂度计算

最新文章

热门文章