其实直接暴力O(n3)DP+O2O(n^3)DP+O_2O(n3)DP+O2优化能过…

CODE O(n3)O(n^3)O(n3)

先来个O(n3)O(n^3)O(n3)暴力DP(开了O2O_2O2)100分代码(极限数据0.5s0.5s0.5s)

#include <cstdio>

#include <cstring>

#include <algorithm>

using namespace std;

const int MAXN = 2005, INF = 0x3f3f3f3f;

int n, m, a[MAXN], f[2][MAXN]; char s[MAXN];

inline void chkmin(int &x, const int &y) { if(y < x) x = y; }

int main () {

	freopen("ni.in", "r", stdin);

	freopen("ni.out", "w", stdout);

	scanf("%d%d", &n, &m);

	for(int i = n; i >= 1; --i) {

		scanf("%s", s + 1);

		for(int j = 1; j <= m; ++j)

			if(s[j] == '*' && !a[j]) a[j] = i;

	}

	int now = 0;

	memset(f[0], 0x3f, sizeof f[0]); f[0][a[1]] = 0; //f[i][j]表示i列消得剩下j个的最小步数,暴力刷表

	for(int i = 1; i <= m; ++i) {

		now ^= 1; memset(f[now], 0x3f, sizeof f[now]);

		for(int j = a[i]; ~j; --j) if(f[now^1][j] != INF)

			for(int k = j>>1; ~k; --k)

				chkmin(f[now][max(a[i+1]+3*k-2*j, 0)], f[now^1][j]+j-k);

	}

	printf("%d\n", f[now][0]);

}

正解

如上面的暴力DP状态定义一样,只是换成了填表,便于考虑决策单调性.

化简后的方程式为

f[i][j]=f[i−1][2A[i]−2j−3k]+A[i]−j−kf[i][j]=f[i-1][2A[i]-2j-3k]+A[i]-j-kf[i][j]=f[i−1][2A[i]−2j−3k]+A[i]−j−k

单调性证明传送门

这句话:

再观察一下可以发现，在jjj确定的时候，F[i−1][2A[i]−2j−3k]+A[i]−j−kF[i−1][2A[i]−2j−3k]+A[i]−j−kF[i−1][2A[i]−2j−3k]+A[i]−j−k的取值是单峰的。因为F[i−1][2A[i]−2j−3k]F[i−1][2A[i]−2j−3k]F[i−1][2A[i]−2j−3k]随k的减小是不增的，A[i]−j−kA[i]−j−kA[i]−j−k是单增的，因此它是单峰的。

感受一下,大概可以这么想:F[i−1][2A[i]−2j−3k]F[i−1][2A[i]−2j−3k]F[i−1][2A[i]−2j−3k]是不降的,我们感受一下,它的导函数应该不会是什么奇怪的形状,而是单调的…

并且A[i]−j−kA[i]−j−kA[i]−j−k是关于kkk的一次函数,导数为常函数.

所以:

"导函数单调 +++ 一次函数(导函数为常函数) →\to→ 单峰函数(导函数单调)."画出来如下

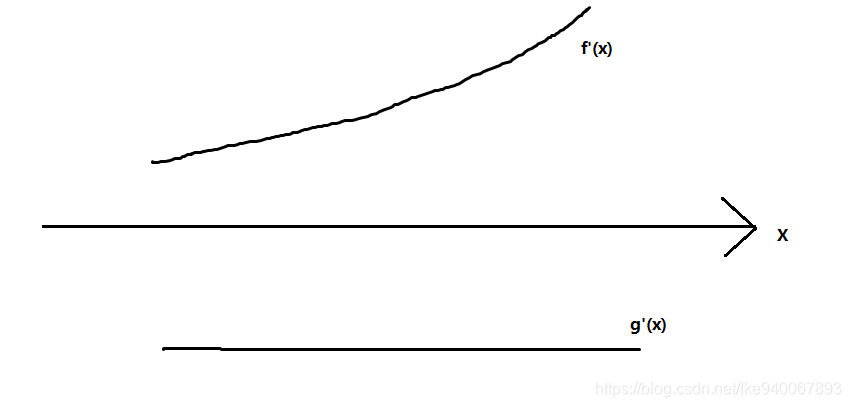
这样的话f′(x)+g′(x)f'(x)+g'(x)f′(x)+g′(x)如果没有穿过xxx轴,就仍是单调函数.

若穿过了xxx轴,比如先为负,然后为000,然后为正,那么体现在图像上就是单峰了…(好像说了一堆废话)

然后就单调队列优化了.具体代码见下(粘来的代码)

CODE O(n2)O(n^2)O(n2)

#include<cstdio>

#include<cstring>

#include<algorithm>

#define maxn 2005

using namespace std;

const int inf = 0x3f3f3f3f;

int n,m,a[maxn],f[2][maxn];

char s[maxn];

inline void chkmin(int &a,int b){if(a>b) a=b;}

int main()

{

	freopen("ni.in","r",stdin);

	freopen("ni.out","w",stdout);

	scanf("%d%d",&n,&m);

	for(int i=n;i>=1;i--){

		scanf("%s",s+1);

		for(int j=1;j<=m;j++) if(s[j]=='*'&&!a[j]) a[j]=i;

	}

	int now=0;memset(f[0],0x3f,sizeof f[0]);

	f[0][0]=0;

	for(int i=1;i<=m;i++,now=!now){

		memset(f[!now],0x3f,sizeof f[!now]);

		for(int j=0;j<=a[i];j++){

			int id=(a[i]-j)>>1;

			for(int k=id;k>=0;k--){

				int x=k+(a[i]-j-2*k)*2;

				if(x>a[i-1]) x=a[i-1];//emmm...

				if(f[!now][j]>=f[now][x]+k+a[i]-j-2*k) id=k,f[!now][j]=f[now][x]+k+a[i]-j-2*k;

				else break;

			}

		}

	}

	printf("%d",f[now][0]);

}

巴特西

Ｎewnode's NOI(P?)模拟赛第二题 dp决策单调优化

CODE O(n3)O(n^3)O(n3)

正解

CODE O(n2)O(n^2)O(n2)

最新文章

热门文章

巴特西

Ｎewnode's NOI(P?)模拟赛 第二题 dp决策单调优化

CODE O(n3)O(n^3)O(n3)

正解

CODE O(n2)O(n^2)O(n2)

最新文章

热门文章

Ｎewnode's NOI(P?)模拟赛第二题 dp决策单调优化