重识线段树——Let's start with the start.
声明
本文为 Clouder 原创,在未经许可情况下请不要随意转载。原文链接
前言
一般地,这篇文章是给学习过线段树却仍不透彻者撰写的,因此在某些简单的操作上可能会一笔带过。
当然了,入门线段树后也可以读此文来尝试进阶、巩固理解,而线段树大师就没有读本文的必要了,无任何高端操作。
笔者亦在写作过程中,重新理解线段树这个神奇的数据结构。
行文并无严格顺序。
概念
线段树是一种广泛用于区间操作的二叉搜索树,易于理解,灵活性高。
相比于暴力的\(O(n)\)复杂度,它的复杂度为\(O(\log n)\),这使它在数据规模大时有着绝对性的优势。
相比于树状数组,它的常数虽然更大,但在算法思想上看,线段树更加直观、清晰(当然是个人观点),在实现较复杂的功能时思路更容易取得,因此笔者相当喜爱这种数据结构。
二分性
这个概念完全是笔者杜撰的,但或许对理解线段树有所帮助。
即在构造线段树时,每个区间都被分为两个区间,直到叶子节点为止。
那么这样构造,线段树就是一棵平衡二叉树。
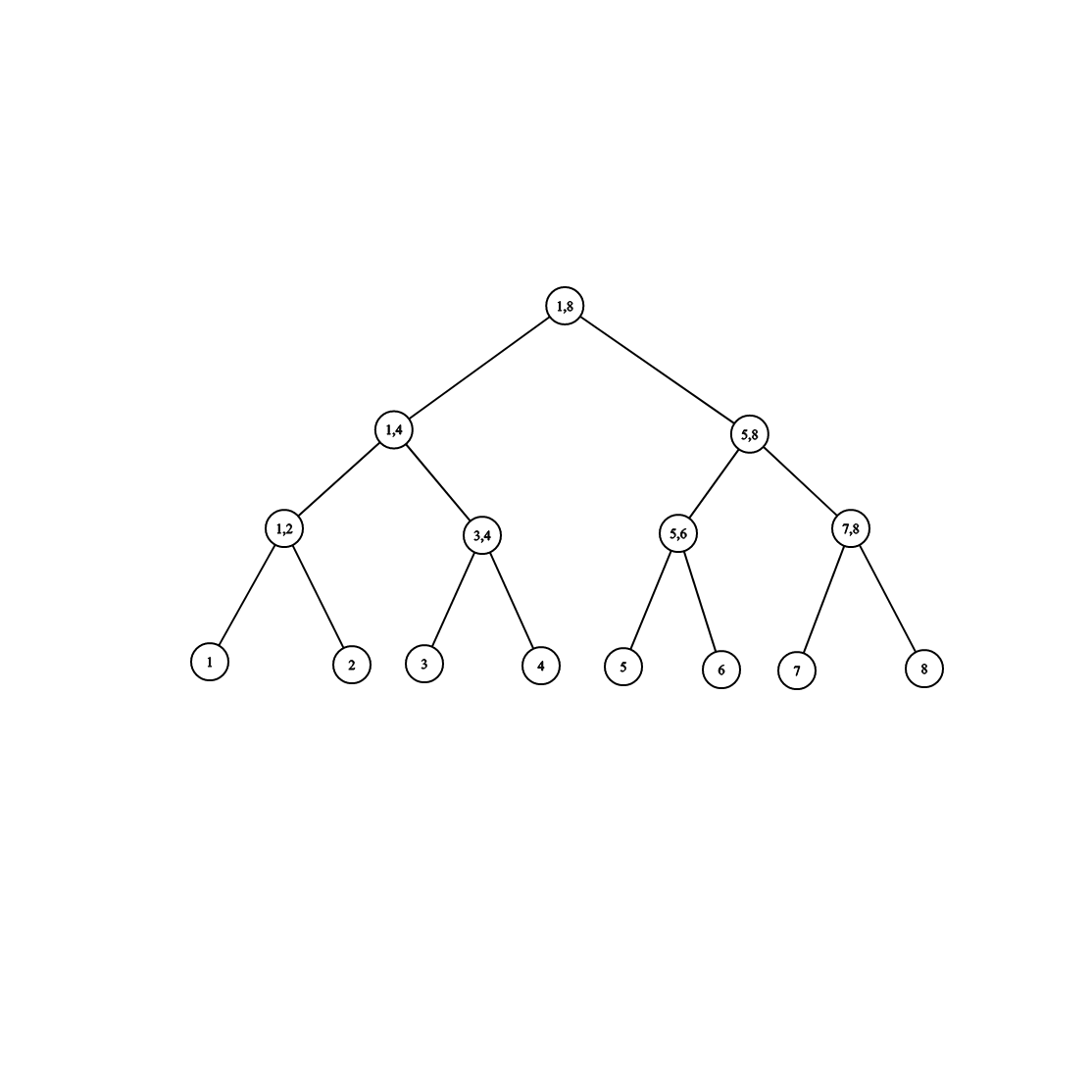
可以发现,当数组的总长为 \(n\) 时,线段树的树高最多是 \(\log n\),这意味着我们从根节点开始寻找目标区间时,最多经过 \(\log n\)个节点。
真的只经过\(\log n\)个节点吗?
我们发现,线段树上的操作大致分为单点操作和区间操作,那么分类讨论一下。
简略的复杂度证明
单点操作
单点操作的复杂度很好证明,因为操作的是叶子结点,那么只需要从根走到叶子,复杂度等同于树高,也就是\(\log n\)。
区间操作
先来看看区间操作的代码:
int ll,rr;
void do(const int &l,const int &r,const int &p)
{
if(ll <= l && rr >= r)
{
dosomething();
return;
}
int mid = l + r >> 1;
push_down(p);
if(ll <= mid)
do(l,mid,p<<1);
if(rr > mid)
do(mid+1,r,p<<1|1);
push_up(p);
}
一个节点,从代码中看出,是有可能即访问左儿子又访问右儿子的。
那如果从根节点,又访问了左儿子又访问了右儿子,一直访问到叶子结点,将全树遍历一遍,复杂度不就爆炸了吗?
笔者尝试了一番,发现这个证明并没有想象中的那么显然。当然可能是笔者实力太弱的缘故。
首先,假定我们正在访问一棵线段树,并且一层层地向下,像 bfs 一样。
每个被访问的点,只有三种情况:目标区间被完全包含,被目标区间完全包含,部分包含目标区间。
将完全包含假定为直接返回,只需要考虑部分包含的节点。
那么访问一次线段树,会有三个阶段。
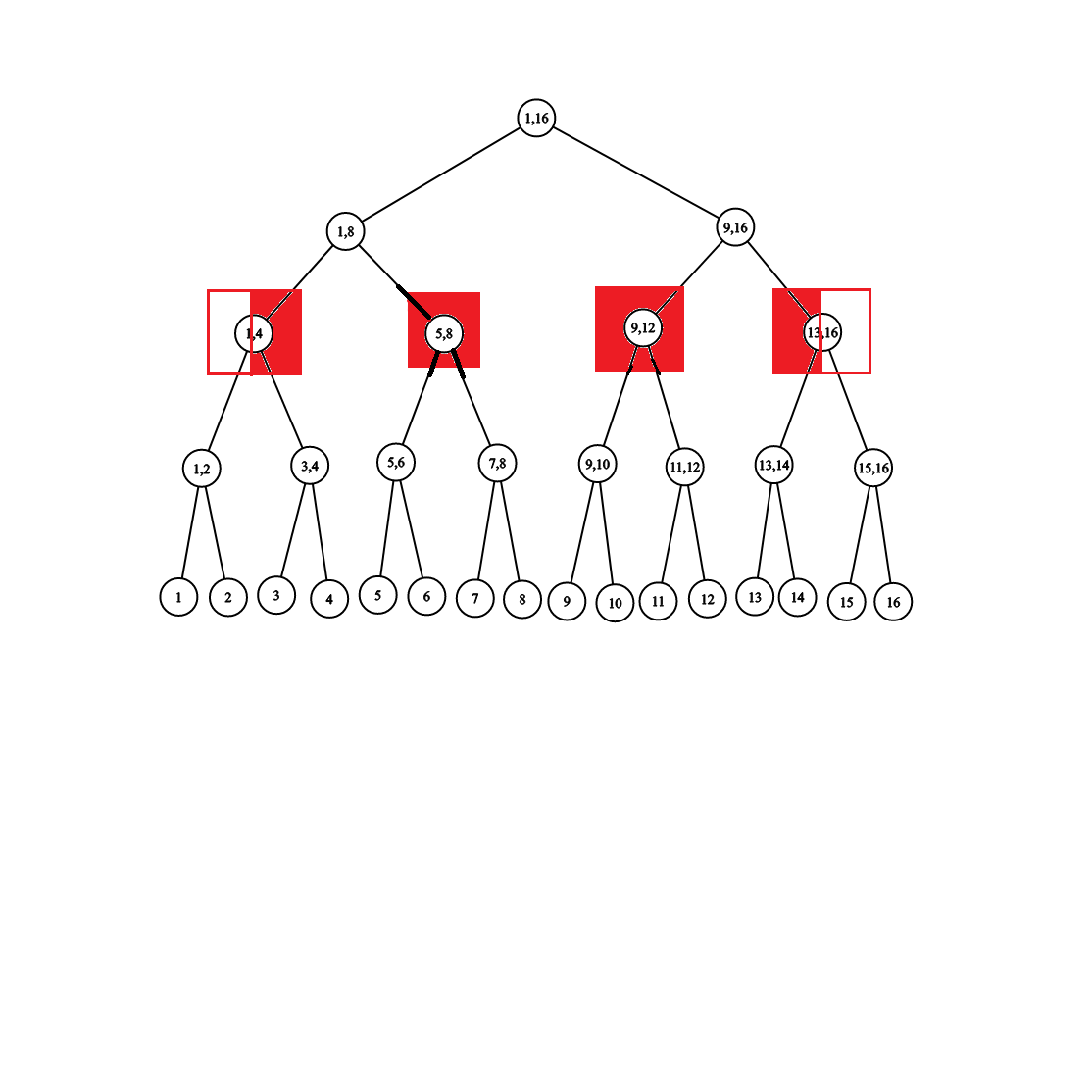
- 节点的某个儿子完全包含目标区间,此时每层只会访问一个节点,不断向下。
- 节点的两个儿子部分包含目标区间。
这种情况只会出现一次,在例子中,这种情况出现在根节点上。
出现后,以中点为界,分成的两个区间,也只有三种情况:
一个儿子被完全包含,一个儿子部分包含,或者一个儿子部分包含,或者一个儿子被完全包含。
前者即 3 中的情况。 - 节点的一个儿子部分包含目标区间,另一个儿子被目标区间完全包含。
即图中 \((1,8)\) 与 \((9,16)\) 的情况。
那么被完全包含的直接返回,而部分包含的继续向下,又是 3 中的情况。
这样,在同一层中最多同时存在 \(2\) 个部分包含的节点和 \(2\) 个完全包含的节点。
由此可见,复杂度就是树高,即 \(n\) 了,即 \(\log _2 \texttt{区间总长度}\)。
在访问线段树时,首先是 1 中的过程,出现 2 后进行一次分叉,随后进入 3 的过程,每层的节点数始终不超过 \(4\)。
假如要卡到最劣复杂度,访问区间即为 \(2,2^n - 1\) ,在上例中为 \(2,15\),读者可以手推一遍感受一下。
笔者水平有限,可能并不严谨,会意即可。
k分线段树
那么问题来了,为什么要划分一个区间为两个子区间呢?
举个例子,为什么不把区间分为三个子区间,成为一个三叉树呢?
直接假定建立一个\(k\)叉的线段树,假定总区间长度为 \(k^n\),树高为 \(n\)。
单点查询的复杂度即为树高,不赘述了。
效仿上文进行复杂度分析:
- 首先,节点的某个儿子完全包含目标区间,一路向下。
- 找到了一个节点,其中某两个儿子部分包含目标区间,夹在中间的儿子被目标区间完全包含。
- 再向下,一个部分包含的儿子会衍生出一个部分包含的儿子和若干个被完全包含的儿子。
其中 2 阶段,最劣情况即 \(k - 2\) 个被完全包含,\(2\)个部分包含,那么该层有 \(k\) 个节点被访问。
而 3 阶段中,一个部分包含的儿子在最劣情况下,有 \(k - 1\) 个被完全包含的儿子,\(1\)个部分包含的儿子,一共访问了 \(k\) 个节点。
如果计算常数的话,那么复杂度就是\(k \log _k n\),此时经过某些计算可以得出在 \(k = \texttt{e}\) 时取得最小值,那么将 \(k\) 限制为整数,取 \(3\) 也应当比取 \(2\) 要优。
在数据规模为 \(10^5\) 时,笔者用计算器算了二者的差距:
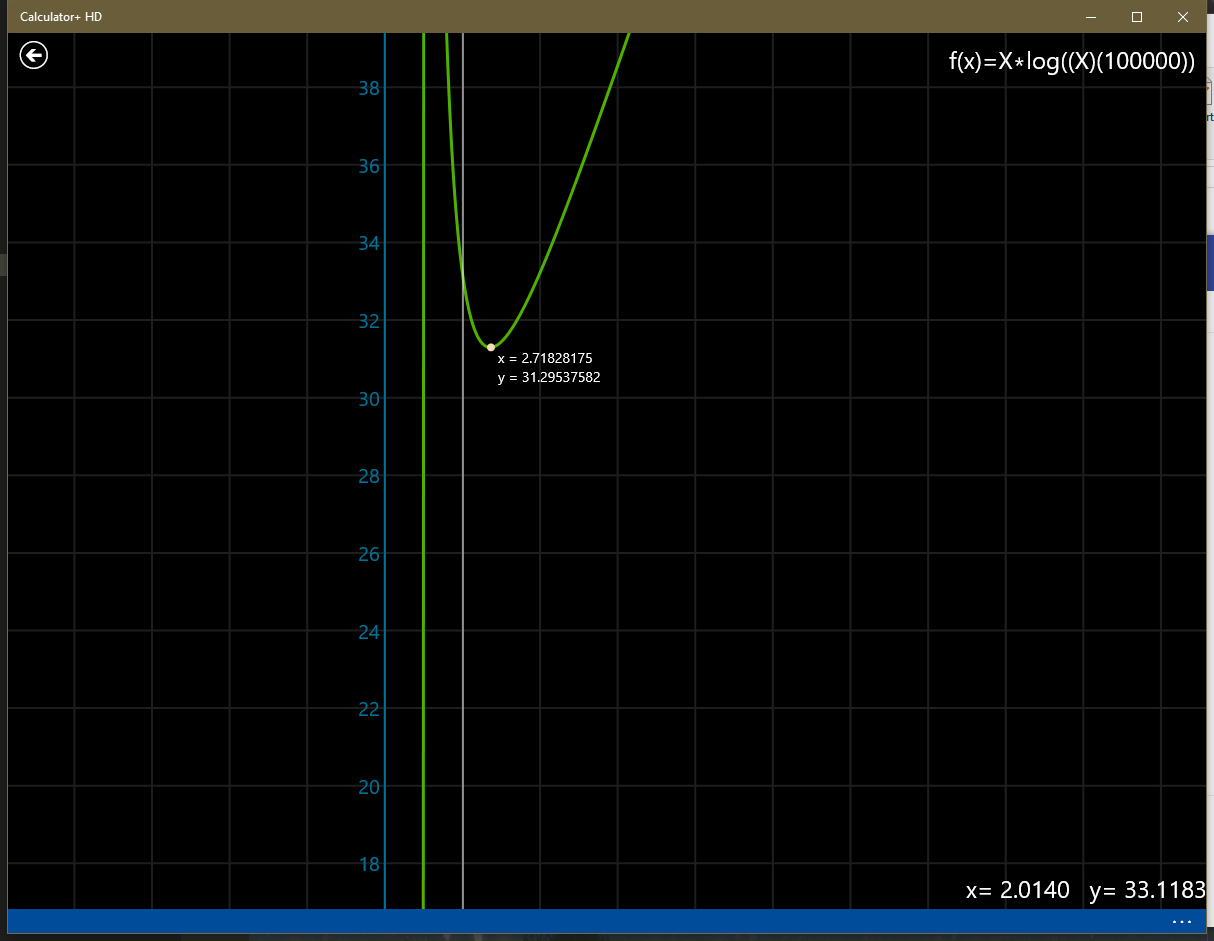
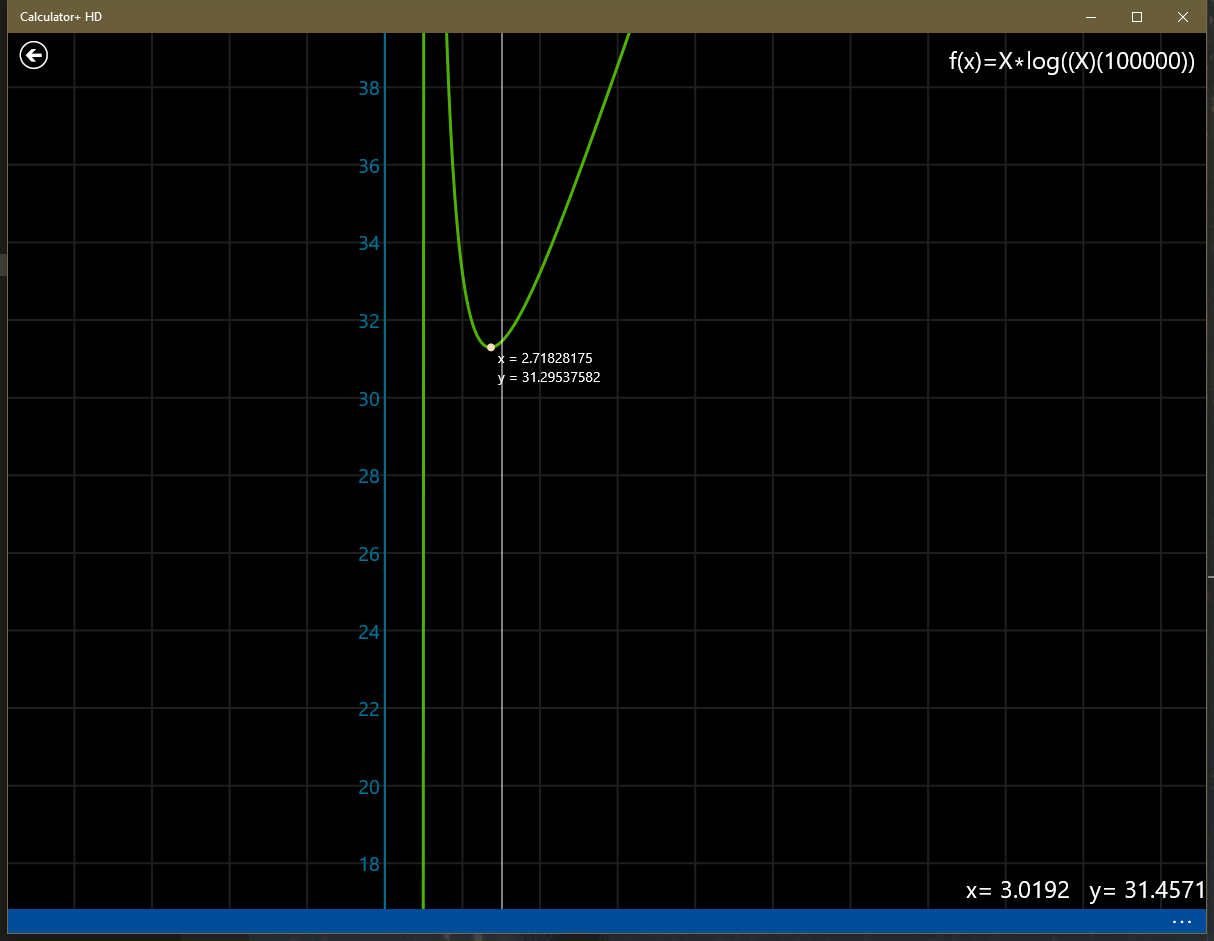
可以看到,单次操作差距大概有 \(5\)%,但事实上跑满非常困难,而且三分会加大常数,因此实际速度如何难以估计。
同时二分线段树的空间也会比三分线段树小。
代码实现如下:
PS:为了方便处理三分,笔者将 \(n\) 扩大到了 \(3\) 的整次幂。为了方便对比,将二叉线段树的 \(n\) 也扩大到了 \(2\) 的整次幂。
#include <cstdio>
using namespace std;
template <typename T>
inline T read(T &r)
{
static char c;
static int flag;
flag = 1, r = 0;
for (c = getchar(); c > '9' || c < '0'; c = getchar())
if (c == '-')
flag = -1;
for (; c >= '0' && c <= '9'; r = (r << 1) + (r << 3) + (c ^ 48), c = getchar())
;
return r *= flag;
}
const int maxn = 1e5 + 100;
struct node
{
long long sum, tag;
int l, r, len, lmid, rmid; //[l,lmid],[lmid+1,rmid],[rmid+1,r]
} a[maxn * 20];
int w[maxn];
int n, m;
inline void push_up(const int &p)
{
a[p].sum = a[p * 3].sum + a[p * 3 + 1].sum + a[p * 3 + 2].sum;
}
inline void push_down(const int &p)
{
node &now = a[p], &ls = a[p * 3], &ms = a[p * 3 + 1], &rs = a[p * 3 + 2];
if (!now.tag)
return;
ls.sum += ls.len * now.tag;
ms.sum += ms.len * now.tag;
rs.sum += rs.len * now.tag;
ls.tag += now.tag;
ms.tag += now.tag;
rs.tag += now.tag;
now.tag = 0;
}
void build(const int &l, const int &r, const int &p)
{
a[p].l = l, a[p].r = r, a[p].len = r - l + 1;
int len = a[p].len / 3;
a[p].lmid = a[p].l + len - 1;
a[p].rmid = a[p].lmid + len;
if (l == r)
{
a[p].lmid = a[p].rmid = a[p].l;
a[p].sum = w[l];
return;
}
build(l, a[p].lmid, p * 3);
build(a[p].lmid + 1, a[p].rmid, p * 3 + 1);
build(a[p].rmid + 1, a[p].r, p * 3 + 2);
push_up(p);
}
void add(const int &p, const int &k, const int &ll, const int &rr)
{
if (ll <= a[p].l && rr >= a[p].r)
{
a[p].sum += a[p].len * k;
a[p].tag += k;
return;
}
push_down(p);
if (ll > a[p].r)
return;
if (rr < a[p].l)
return;
int lp = 0;
if (ll <= a[p].lmid)
add(p * 3, k, ll, rr), lp = 1;
else if (ll <= a[p].rmid)
add(p * 3 + 1, k, ll, rr), lp = 2;
else
add(p * 3 + 2, k, ll, rr), lp = 3;
if (rr > a[p].rmid && lp != 3)
add(p * 3 + 2, k, ll, rr);
else if (rr > a[p].lmid && lp != 2)
add(p * 3 + 1, k, ll, rr);
else if (lp != 1)
add(p * 3, k, ll, rr);
if (lp == 1 && rr > a[p].rmid)
add(p * 3 + 1, k, ll, rr);
push_up(p);
}
long long ask(const int &p, const int &ll, const int &rr)
{
if (ll <= a[p].l && rr >= a[p].r)
return a[p].sum;
if (ll > a[p].r)
return 0;
if (rr < a[p].l)
return 0;
push_down(p);
long long ans = 0;
int lp = 0;
if (ll <= a[p].lmid)
ans += ask(p * 3, ll, rr), lp = 1;
else if (ll <= a[p].rmid)
ans += ask(p * 3 + 1, ll, rr), lp = 2;
else
ans += ask(p * 3 + 2, ll, rr), lp = 3;
if (rr > a[p].rmid && lp != 3)
ans += ask(p * 3 + 2, ll, rr);
else if (rr > a[p].lmid && lp != 2)
ans += ask(p * 3 + 1, ll, rr);
else if (lp != 1)
ans += ask(p * 3, ll, rr);
if (lp == 1 && rr > a[p].rmid)
ans += ask(p * 3 + 1, ll, rr);
return ans;
}
int main()
{
read(n);
read(m);
for (int i = 1; i <= n; ++i)
read(w[i]);
int nn = 1;
for (nn = 1; nn < n; nn *= 3)
;
build(1, nn, 1);
int opt, x, y, k;
while (m--)
{
read(opt);
read(x);
read(y);
if (opt == 1)
{
read(k);
add(1, k, x, y);
}
else
printf("%lld\n", ask(1, x, y));
}
return 0;
}
同时附上用于对比的二叉线段树代码:
#include <cstdio>
using namespace std;
template <typename T>
inline T read(T &r)
{
static char c;
static int flag;
flag = 1, r = 0;
for (c = getchar(); c > '9' || c < '0'; c = getchar()) if (c == '-') flag = -1;
for (; c >= '0' && c <= '9'; r = (r << 1) + (r << 3) + (c ^ 48), c = getchar());
return r *= flag;
}
const int maxn = 1e5 + 100;
struct node
{
long long sum, tag;
int l, r, len, mid;
} a[maxn * 20];
int w[maxn];
int n, m;
inline void push_up(const int &p)
{
a[p].sum = a[p * 2].sum + a[p * 2 + 1].sum;
}
inline void push_down(const int &p)
{
node &now = a[p], &ls = a[p * 2], &rs = a[p * 2 + 1];
if (!now.tag)
return;
ls.sum += ls.len * now.tag;
rs.sum += rs.len * now.tag;
ls.tag += now.tag;
rs.tag += now.tag;
now.tag = 0;
}
void build(const int &l, const int &r, const int &p)
{
a[p].l = l, a[p].r = r, a[p].len = r - l + 1;
a[p].mid = (l + r) >> 1;
if (l == r)
{
a[p].sum = w[a[p].l];
return;
}
build(l, a[p].mid, p << 1);
build(a[p].mid + 1, r, p << 1 | 1);
push_up(p);
}
void add(const int &p, const int &k, const int &ll, const int &rr)
{
if (ll <= a[p].l && rr >= a[p].r)
{
a[p].sum += a[p].len * k;
a[p].tag += k;
return;
}
push_down(p);
if (ll <= a[p].mid)
add(p << 1, k, ll, rr);
if (rr > a[p].mid)
add(p << 1 | 1, k, ll, rr);
push_up(p);
}
long long ask(const int &p, const int &ll, const int &rr)
{
if (ll <= a[p].l && rr >= a[p].r)
return a[p].sum;
push_down(p);
long long ans = 0;
if (ll <= a[p].mid)
ans = ask(p << 1, ll, rr);
if (rr > a[p].mid)
ans += ask(p << 1 | 1, ll, rr);
return ans;
}
int main()
{
read(n);
read(m);
for(int i = 1;i<=n;++i)
read(w[i]);
int nn = 1;
for(;nn<n;nn*=2);
build(1, nn, 1);
int opt, x, y, k;
while (m--)
{
read(opt);
read(x);
read(y);
if (opt == 1)
{
read(k);
add(1, k, x, y);
}
else
printf("%lld\n", ask(1, x, y));
}
return 0;
}
经过对比,同样写法下,二叉线段树在 \(10^5\) 的数据量下时空都稳定优于三叉线段树。
并且经过实践,笔者发现三叉线段树写起来较为繁琐,有些问题不好处理。
所以说,运行在二进制环境中的计算机上,还是写二叉线段树吧。
指不定以后有变化呢,逃
多标记
待更新。
优先顺序
互相影响性
扫描线
可持久化
最新文章
- java文件压缩和解压
- C++工程编译之“error LNK2001: 无法解析的外部符号”
- CCNA第一讲笔记
- 面向对象程序设计-C++_课时24多态的实现
- Cocos2dx项目移植Android平台
- 一天搞定HTML----常用标签01
- hdu_1564: Play a game
- Erlang游戏服设计总结
- Android的图片,字符串,demin,color,以及Array,boolean,Integer资源的使用-android学习之旅(五十四)
- 正确截取List指定位置的内容
- 自定义Label控件
- RNN知识点
- Django用户验证框架
- Java多线程之内存可见性和原子性:Synchronized和Volatile的比较
- cdoj第13th校赛初赛F - Fabricate equation
- [转] geochart 地图控件官方示例
- python基本算法
- SocketSessionConfig参数设制
- 常用API(Object、String、StringBuffer、用户登陆注册)
- Java WebService一个构建